Основные предпосылки и понятия
1. При чистом изгибе поперечные сечения балки поворачиваются, оставаясь плоскими (гипотеза плоских сечений Я. Бернулли). В этом случае любой продольный элемент балки (в пределе любое волокно) испытывают только осевое растяжение или сжатие, а любая горизонтальная площадка свободна от напряжений, то есть соседние волокна не давят друг на друга и имеет место линейное напряженное состояние.
2. Так как при изгибе балки ее продольные волокна удлиняются с выпуклой стороны и укорачиваются с вогнутой, то, стало быть, должен существовать промежуточный слой волокон, который не удлиняется и не укорачивается, то есть остается не ненапряженным.
Слой ненапряженных волокон называется нейтральным слоем (рис. 9.2).
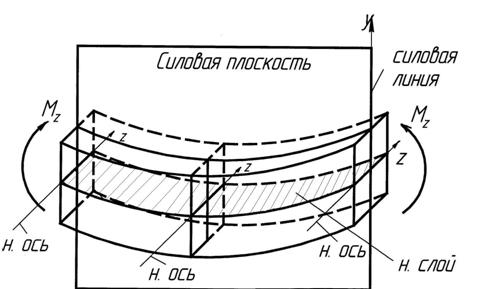
Рис. 9.2 К обоснованию используемых понятий
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью (z).
Таким образом, нейтральная ось есть геометрическое место точек, в которых нормальные напряжения равны нулю.Вокруг нейтральной оси происходит поворот сечений при изгибе.
Если все нагрузки лежат в одной силовой плоскости, то линия пересечения этой плоскости с плоскостью поперечного сечения называется силовой линией (y). Она проходит через центр тяжести сечения, так как плоскость действия нагрузки проходит через ось стержня.
Если сечение имеет хотя бы одну ось симметрии и силовая линия совпадает с этой осью, то нейтральная линия перпендикулярна силовой. Следовательно, сопряженные оси y и z являются главными центральными осями инерции сечения, что будет доказано ниже.
|
|
|
Вывод формулы нормальных напряжений при
Чистом изгибе
Вывод ведут в следующем порядке (рис. 9.3)
1. Вырежем в зоне чистого изгиба балки двумя бесконечно близко расположенными плоскостями 1-1 и 2-2 элемент длиной dx (см. рис. 9.1 и 9.3).
2. Обозначим оси: x – продольная ось стержня, y– ось, совпадающая с силовой линией (и являющаяся осью симметрии сечения), z– ось, совпадающая с нейтральной.
3. Будем считать сечение 1-1 условно неподвижным, тогда сечение 2-2 под действием момента 
повернется вокруг нейтральной оси z на угол 
.
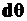4. Отрезок нейтрального слоя, имевший первоначальную длину dx, изогнется, оставаясь ненапряженным, то есть дуга 
может быть определена через центральный угол dq (см. рис. 9.3) и радиус кривизны нейтрального слоя r
. (1П)
Рис. 9.3 К выводу формулы нормальных напряжений при изгибе
5. Произвольное волокно элемента, отстоящее от нейтральной оси zна ординату 
, также имело первоначальную длину dx.Поддействием изгибающего момента оно получило абсолютное удлинение, которое может быть определено через центральный угол dq и радиус у
|
|
|
. (2П)
6. С использованием формул (1П) и (2П) может быть найдено относительное удлинение произвольного волокна
(3П)
7. Так как деформации малы, напряжения не должны превышать предела пропорциональности, а по принятому допущению 
и 
, может быть использован закон Гука для линейного напряженного состояния
или 
, (4П)
где 
- постоянная величина.
По формуле (4П) нельзя еще подсчитать нормальные напряжения, так как неизвестен масштабный коэффициент с и положение в сечении нейтральной оси z,от которой отсчитываются ординаты у. Вместе с тем из этой формулы следует, что нормальные напряжения в точках сечения пропорциональны удалению этих точек (у) от нейтральной оси z(см. рис. 9.3 – эпюру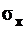 
).
8. Для определения масштабного коэффициента с и положения нейтральной оси zрассмотрим равновесие вырезанного элемента (см. рис 9.3)
|
|
|
; внешних продольных сил нет, поэтому можно суммировать по всей площади сечения только элементарные продольные силы 
, то есть
. (5П)
Подставляя в (5П) значение 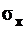из формулы (4П), получим
, но 
, поэтому 
,
а это не что иное, как статический момент поперечного сечения относительно оси z,то есть
. (6П)
Равенство 
нулю говорит о том, что нейтральная ось z проходит через центр тяжести сечения.
; Внешних изгибающих моментов относительно оси y нет, следовательно, можно просуммировать только моменты элементарных продольных сил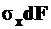 
относительно этой оси
. (7П)
Снова подставляя в эту формулу значение 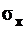из (4), получим 
, но , поэтому 
. Этот интеграл носит название центробежного момента инерции сечения и обозначается 
, то есть
. (8П)
Из теории геометрических характеристик плоских сечений известно, что в том случае, когда 
, оси y и z являются главными центральными осями инерции сечения. Это тем более верно потому, что по условию ось yявлялась осью симметрии, которая всегда является главной осью инерции сечения (см. учебную литературу, приведенную в списке).
|
|
|
; Здесь имеют место внешний (условно) изгибающий момент 
и моменты элементарных сил 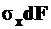относительно этой оси, то есть
. (9П)
Снова подставляя в эту формулу значение 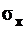из формулы (4), получим
.
Интеграл вида 
называется моментом инерции сечения относительно оси zи обозначается через 
, то есть
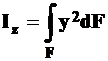. (10П)
, так же, как и , является геометрической характеристикой сечения, не имеющей физического смысла. Она имеет размерность длины в четвертой степени. Таким образом,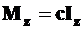 
и
. (11П)
Подставляя это значение с в формулу (4П), получим
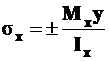, (9.1)
то есть нормальное напряжение при изгибе в любой точке поперечного сечения пропорционально изгибающему моменту, расстоянию точки от нейтральной оси z и обратно пропорционально главному центральному моменту инерции поперечного сечения. Знак плюс или минус перед формулой ставится по физическому смыслу: если волокно растянуто – плюс, если сжато – минус.
Лекция 10
Дата добавления: 2018-02-15; просмотров: 480; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!