Обобщение формул потенциальной энергии для простых
Напряженных состояний. Метод определения перемещений
Б.П.Э. Клапейрона
Подведем итог того, что известно из первой части курса о потенциальной энергии в случаях простых напряженных состояний:
- потенциальная энергия при растяжении-сжатии равна
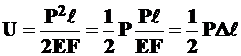; (12.6)
- потенциальная энергия при кручении равна
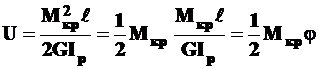; (12.7)
- потенциальная энергия при чистом изгибе равна
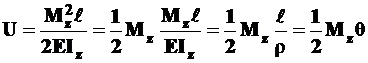; (12.8)
- элементарная потенциальная энергия при сдвиге (срезе) на участке 
равна
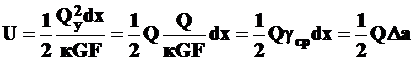. (12.9)
Обобщая формулы (12.8…12.11), можно сделать следующие выводы:
1) потенциальная энергия деформации численно равна половине произведения обобщенной силы (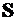 
) на соответствующее ей перемещение ( 
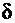), то есть
. (12.10)
“Соответствие” заключается в том, что речь идет о перемещении того сечения, где приложена сила, причем о таком перемещении, что произведение его на эту силу дает величину работы.
Таким образом, сосредоточенной силе соответствует линейное перемещение в точке ее приложения и по ее направлению. Изгибающему моменту соответствует угол поворота того сечения, где он приложен.
Формула (12.10) может быть использована для вычисления соответствующих перемещений лишь в том случае, когда к балке приложена лишь одна независимая внешняя сила или один момент, причем в том месте, где они приложены. Тогда из (12.13)
|
|
|
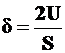. (12.11)
Эта формула носит имя Б. П. Э. Клапейрона.
2) Потенциальная энергия есть функция второй степени от независимых внешних сил, поэтому при использовании формулы Клапейрона необходимо выражать реакции опор через независимые внешние силы, то есть практически решать задачи надо вначале в буквенном виде.
Следует отметить, что при применении метода Клапейрона и других методов, которые будут рассмотрены ниже и носящих наименование “энергетических”, знак перемещения получается положительным, если его направление совпадает с направлением соответствующей независимой внешней силы или момента, и что отсчет абсцисс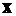 
силовых участков можно производить от любого начала координат.
Рассмотрим примеры применения метода Клапейрона.
Можно найти только прогиб в точке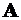 
.
Пример 1.
Рис. 12.2 К примеру определения прогиба медом Клапейрона
.
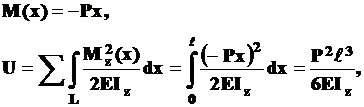
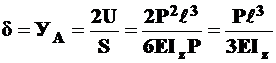Получили знакомый прогиб, но со знаком плюс.
Пример 2.
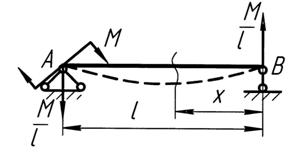
Рис. 12.3 К примеру определения угла поворота методом Клапейрона
|
|
|
Можно найти только угол поворота в точке .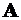
.
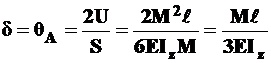В этом примере получили знакомый угол поворота сечения, но со знаком плюс.
Как видно, метод Клапейрона проще, но его возможности крайне ограничены по сравнению с методом непосредственного интегрирования.
Лекция 13
Метод определения перемещений Д. К. Максвелла - О. Мора
Одним из наиболее удобных и часто применяемых методов определения перемещений является метод Максвелла –Мора. Рабочее уравнение этого метода записывается в следующем виде:
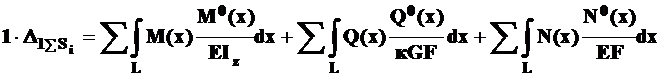. (13.1)
Уравнение (13.1) часто называют интегралами Максвелла – Мора (1864-1874) или просто интегралами Мора, так как он ввел этот метод в практику расчета конструкций. В нем:
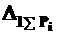- искомое перемещение (линейное или угловое) в точке приложения силы или момента; равных единице, и по их направлению от действия всей внешней нагрузки, приложенной к системе (например, к балке, раме и т.д.);
, 
и 
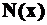- уравнения изгибающих моментов, поперечных и продольных сил на силовых участках системы от внешней нагрузки;
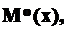
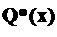и 
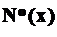- уравнения изгибающих моментов, поперечных и продольных сил на тех же силовых участках системы от единичной нагрузки.
Физический смысл формулы (13.1):
Дата добавления: 2018-02-15; просмотров: 450; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!