Расчет на жесткость при изгибе. Определение перемещений
В балках постоянного сечения методом непосредственного
Интегрирования
Расчеты на жесткость при изгибе связаны с определением перемещений опасных сечений балки, а затем их ограничением. Действительно, под действием внешних сил ось балки искривляется в силовой плоскости, в результате чего ее точки перемещаются (рис. 11.1).
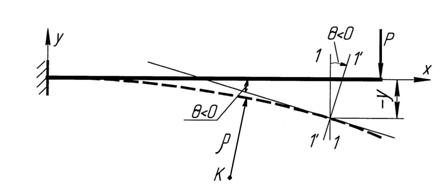
Рис. 11.1 К выводу дифференциального уравнения изогнутой оси балки
Изогнутая ось балки называется упругой линией, а вертикальные проекции ее точек (проекции на ось у) называются прогибами и обозначаются через у.
Прогибы будут считаться положительными, если точки оси смещаются вверх относительно х.
При деформации балки ее поперечные сечения (например, 1-1) не только поступательно смещаются, но и поворачиваются (1¢-1¢). Пренебрегая деформациями сдвига, можно считать угол поворота сечения  равным углу между касательной, проводимой к изогнутой оси балки в этом сечении, и первоначально прямой осью балки. В дальнейшем будет определяться именно этот угол (рис. 11.1), поэтому надо помнить, что он равен углу поворота сечения.
равным углу между касательной, проводимой к изогнутой оси балки в этом сечении, и первоначально прямой осью балки. В дальнейшем будет определяться именно этот угол (рис. 11.1), поэтому надо помнить, что он равен углу поворота сечения.
Угол поворота будем читать положительным, если сечение при деформации поворачивается против хода часовой стрелки. Таким образом, необходимо уметь определить прогибы и углы поворота сечений балки.
Вспомним, что при выводе формул нормальных напряжений при изгибе было получено два выражения для постоянной с.
|
|
|
 (1П) и
(1П) и  (2П)
(2П)
Приравнивая правые части уравнений (1П) и (2П), получим
 (3П)
(3П)
Из курса высшей математики известна зависимость между радиусом кривизны (кривизной) плоской кривой и координатами х и у ее точек.
 . (4П)
. (4П)
Если пренебречь величиной  , так как угол поворота сечения мал и, тем более, мал квадрат его величины, то с достаточной для инженерных расчетов точностью можно записать, приравнивая правые части уравнений (3П) и (4П), следующее выражение
, так как угол поворота сечения мал и, тем более, мал квадрат его величины, то с достаточной для инженерных расчетов точностью можно записать, приравнивая правые части уравнений (3П) и (4П), следующее выражение
 , (11.1)
, (11.1)
где  - вторая производная,
- вторая производная, 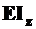 - жесткость при изгибе,
- жесткость при изгибе,
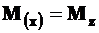 - уравнение изгибающего момента на соответствующем силовом участке балки
- уравнение изгибающего момента на соответствующем силовом участке балки
Уравнение (11.1) называется основным дифференциальным уравнением изогнутой оси балки. В нем знак плюс стоит потому, что положительное значение  совпадает с
совпадает с  >
>  , так как кривая вогнутая, и наоборот.
, так как кривая вогнутая, и наоборот.
Проинтегрировав выражение (11.1), получим уравнение углов поворота сечения
 . (11.2)
. (11.2)
Интегрируя второй раз, получим уравнение прогибов
 . (11.3)
. (11.3)
|
|
|
Из выражений (11.1 – 11.3) следует, что каждый силовой участок балки будет иметь свое дифференциальное уравнение своей части изогнутой оси балки и, следовательно, свои постоянные С и D. Существуют правила, при соблюдении которых, вне зависимости от числа силовых участков, все постоянные Сбудут равны между собой и все постоянные D также равны между собой. Эти правила таковы:
1. Отсчет абсцисс всех силовых участков балки следует производить от крайнего левого или правого центра тяжести сечения балки, помещая туда начала координат (рис. 11.2).
2. Если на схеме балки имеется распределенная нагрузка, обрывающаяся где-то на ее длине (например, на участке а, рис 11.2), то ее надо продлить до конца балки (на участок b), добавляя одновременно нагрузку той же интенсивности, но обратного знака.
3. Если на схеме балки имеется сосредоточенный изгибающий момент, то при написании уравнения изгибающих моментов его надо умножить на скобку
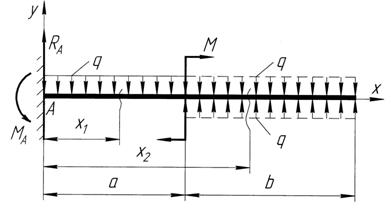
Рис. 11.2 К доказательству возможности равенства
постоянных интегрирования
множитель  , то есть
, то есть  , где а – расстояние от начала координат до точки приложенного момента.
, где а – расстояние от начала координат до точки приложенного момента.
4. Интегрирование уравнения изгибающих моментов надо производить, не раскрывая скобок, т.е методом замены переменных, например,
|
|
|
 .
.
При соблюдении перечисленных правил постоянных остается две – С и D. Их можно определить из условий на границе соседних участков и условий закрепления на опорах, то есть
- на границе двух участков прогиб и угол поворота сечения одинаковы для обоих участков;
- в заделке прогиб и угол поворота равны нулю;
- на шарнирных опорах прогибы равны нулю.
Покажем справедливость изложенных правил на примере (рис. 11.2).
1-й участок.
 (1П)
(1П)
 (2П)
(2П)
 (3П)
(3П)
2-й участок.
 ; (4П)
; (4П)
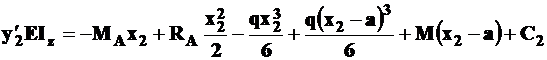 ; (5П)
; (5П)
 .(6П
.(6П
Используем условия на границе двух участков:
При 
 приравнивая правые части уравнений (2П) и (5П), получим
приравнивая правые части уравнений (2П) и (5П), получим
 .
.
При 
 Приравнивая правые части уравнений (3П) и (6П), получим
Приравнивая правые части уравнений (3П) и (6П), получим
 .
.
Таким образом, доказано, что при соблюдении перечисленных выше правил, все С равны между собой и все D равны между собой. Найдем их.
При 
 Из уравнения (2) в общем виде получим
Из уравнения (2) в общем виде получим
 (11.4)
(11.4)
то есть физический смысл С – это угол поворота в начале координат  , умноженной на жесткость. В конкретном примере
, умноженной на жесткость. В конкретном примере  и, значит,
и, значит, 
|
|
|
При  и
и 
 . Из уравнения (3) в общем виде получим
. Из уравнения (3) в общем виде получим
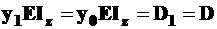 , (11.5)
, (11.5)
то есть физический смысл D –это прогиб в начале координат 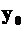 , умноженной на жесткость. В рассматриваемом примере
, умноженной на жесткость. В рассматриваемом примере  и, значит,
и, значит, 
Найдя  и
и  , можно вычислить углы поворота сечения, используя промежуточные уравнения (2П) и (5П), и прогибы, - используя уравнения (3П) и (6П). Для этого в уравнения необходимо подставить лишь соответствующие значения
, можно вычислить углы поворота сечения, используя промежуточные уравнения (2П) и (5П), и прогибы, - используя уравнения (3П) и (6П). Для этого в уравнения необходимо подставить лишь соответствующие значения 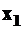 и
и  .
.
Рассмотрим еще один более простой пример (рис. 11.3). Необходимо найти методом непосредственного интегрирования прогиб и угол поворота конца консоли, нагруженной силой 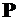 .
.
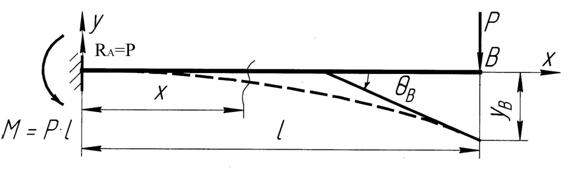
Рис. 11.3 Пример определения перемещений методом непосредственного интегрирования
 (1П)
(1П)
 (2П)
(2П)
 (3П)
(3П)
Условие в заделке: при  ,
,  то есть
то есть  ;
;
при  и
и  то есть
то есть 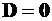 .
.
 найдем при
найдем при 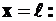
 и
и  . (4П)
. (4П)
 найдем также при
найдем также при 
 и
и  . (5П)
. (5П)
Как видно, знаки при  и
и  соответствуют правилу.
соответствуют правилу.
В заключение следует отметить, что недостатком метода непосредственного интегрирования является необходимость интегрирования дифференциальных уравнений по участкам, достоинством – возможность нахождения углов поворота и прогибов любых сечений балки.
Лекция 12
Потенциальная энергия изгиба
Пусть балка работает на чистый изгиб, тогда в ее поперечном сечении возникает только изгибающий момент  (рис. 12.1).
(рис. 12.1).
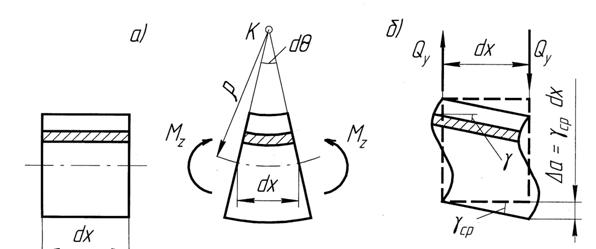
Рис. 12.1 К выводу формул для подсчета потенциальной энергии изгиба
Выделим из балки элемент длиной  , ограниченный двумя поперечными сечениями, которые в результате изгиба взаимно повернулись на угол
, ограниченный двумя поперечными сечениями, которые в результате изгиба взаимно повернулись на угол 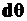 .
.
При статическом способе приложения нагрузки элементарная работа внутренних сил (потенциальная энергия) в этом элементе будет равна
 , (12.1)
, (12.1)
но  , а
, а  ,
,
 .
.
Так как при чистом изгибе  , то полная работа внутренних сил, численно равная потенциальной энергии, накапливаемой элементом длиной
, то полная работа внутренних сил, численно равная потенциальной энергии, накапливаемой элементом длиной 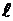 (принцип Ж.Л. Лагранжа), выразится формулой
(принцип Ж.Л. Лагранжа), выразится формулой
 (12.2)
(12.2)
В общем случае изгиба в сечениях балки возникают изгибающий момент и поперечная сила и, кроме того, изгибающий момент меняется по длине балки.
Работа изгибающего момента выразится суммой интегралов
 (12.3)
(12.3)
распространенной на всю длину балки L. В числителе интеграла стоит возведенное в квадрат уравнение изгибающего момента на соответствующем силовом участке балки. Таким образом, для получения величины полной потенциальной энергии необходимо подсчитать сумму интегралов, выражающих потенциальную энергию изгиба всех участков балки.
Работу поперечных сил (работу среза) можно вычислить следующим образом. Снова рассмотрим элемент длиной  (см. рис. 12.1) и выделим в нем тонкий продольный слой. Под действием
(см. рис. 12.1) и выделим в нем тонкий продольный слой. Под действием  весь элемент получит сдвиг на угол
весь элемент получит сдвиг на угол  , который представляет собой некоторое среднее значение из углов сдвига отдельных слоев, определяемых по закону Гука при сдвиге
, который представляет собой некоторое среднее значение из углов сдвига отдельных слоев, определяемых по закону Гука при сдвиге
 , (1П)
, (1П)
так как касательное напряжение меняется по высоте сечения по закону параболы (см. вывод формулы Журавского).
Среднему значению угла сдвига будет соответствовать среднее касательное напряжение
 , (2П)
, (2П)
которое в то же время равно
 . (3П)
. (3П)
Коэффициент котличается от единицы, так как напряжение, соответствующее среднему углу сдвига, не есть среднее арифметическое значение напряжений. Коэффициент к зависит от формы поперечного сечения. Так, для прямоугольного профиля он равен 5/6, для круга – 0,85, для двутавра 0,3…0,4 (отношение  к
к  ).
).
Запишем выражение элементарной энергии среза для элемента балки длиной  при статическом способе приложения нагрузки
при статическом способе приложения нагрузки
 . (12.4)
. (12.4)
Если приравняем правые части формул (2П) и (3П), то получим
 . (5П)
. (5П)
Подставляя значение  в формулу (4П), получим
в формулу (4П), получим
 . (6П)
. (6П)
Полная потенциальная энергия среза с учетом возможного изменения  по длине балки будет равна
по длине балки будет равна
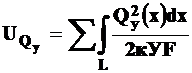 . (12.4)
. (12.4)
Полная потенциальная энергия при поперечном изгибе выразится суммой интегралов
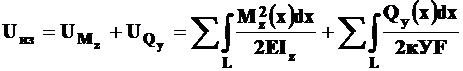 , (12.5)
, (12.5)
где  - уравнение поперечной силы на соответствующем силовом участке балки.
- уравнение поперечной силы на соответствующем силовом участке балки.
Значением  часто пренебрегаю, так как доля ее в
часто пренебрегаю, так как доля ее в  мала.
мала.
Дата добавления: 2018-02-15; просмотров: 747; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
