Поперечная сила в сечении балки численно равна алгебраической сумме внешних поперечных сил, действующих по одну сторону от сечения.
При написании уравнений поперечных сил Q(x)по силам, находящимся
слева от сечения, любую внешнюю силу будем считать положительной, если она направлена вверх (рис. 8.2). При написании уравнений поперечных сил по силам, находящимся справа от сечения, любую внешнюю силу будем считать положительной, если она направлена вниз (рис. 8.2).
Рис. 8.2 Знаки поперечных сил
Изгибающий момент в сечении балки численно равен алгебраической сумме моментов внешних сил, действующих по одну сторону, относительно центра тяжести сечения.
При написании уравнения изгибающих моментов М(х) по действию сил, находящихся слева от сечения, момент любой внешней силы относительно центра тяжести сечения будем считать положительным, если он обуславливает вращение левой части балки по часовой стрелке (рис. 8.3).
При написании уравнений изгибающих моментов по действию сил, находящихся справа от сечения, момент любой внешней силы относительно центра тяжести сечения будем считать положительным, если он обуславливает вращение правой части балки против часовой стрелки (рис. 8.3).
Рис. 8.3 Знаки изгибающих моментов
Дифференциальные зависимости между М, Q и q
(теорема Д. И. Журавского)
Рассмотрим произвольное сечение балки, находящееся на расстоянии х от опоры А (рис. 8.4), и напишем выражение для Q(х) и М(х) – уравнения поперечных сил и изгибающих моментов.
(1П)
|
|
|
. (2П)
Если абсцисса хполучит приращение dx, то Q(х) и М(х) также получат приращение.
; (3П)
Рис. 8.4 К выводу теории Журавского
. (4П)
Вычтем сначала из уравнения (3П) уравнение (1П). Получим
или 
, (8.1)
т. е. первая производная от уравнения поперечной силы по абсциссе сечения равна интенсивности равномерно распределенной нагрузки со знаком минус.
Вычтем затем из уравнения (4П) уравнение (2П). Получим, приравнивая 
нулю, как величину второго порядка малости, выражение
или 
, (8.2)
то есть первая производная от уравнения изгибающего момента по абсциссе сечения равна уравнению поперечной силы.
Выражение (8.2) имеет большое практическое значение, так как позволяет определить положение экстремальной точки на эпюре изгибающих моментов, а затем величину соответствующего момента. В этом есть необходимость тогда, когда балка нагружена распределенной нагрузкой, а на эпюре Qx наклонная прямая, ограничивающая ее, проходит через нуль (см. ниже пример построения эпюр).
Построение эпюр поперечных сил и изгибающих моментов
|
|
|
Рассмотрим пример построения эпюр, основываясь на правилах, изложенных выше (рис. 8.5).
Рис. 8.5 Пример расчета балки на изгиб
Определяем опорные реакции
откуда
откуда
.
Разбиваем схему балки на силовые участки (их три), записываем выражения для Q(х) и М(х) по участкам и подсчитываем численные значения Qи M на их границах.
Участок.
,
.
Обращаем внимание на то, что наклонная прямая, ограничивающая эпюру 
, проходит через ноль. Это означает, что на эпюре 
надо искать точку экстремума. Найдем ее
, 
.
Подставляем значение 
в уравнение и найдем значение, соответствующее точке экстремума
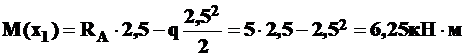
Участок.
,
при х2=0м 
, при х2=2м 
.
Участок.
,
.
На этом участке также имеется точка экстремума.
Действительно. 
, то есть 
=0, а 
3кН×м.
В расчет на прочность принимают наибольшую по абсолютной величине ординату из эпюры изгибающих моментов. В нашем примере – это 6,25 тм.
Следует обратить внимание на то, что скачки на эпюрах 
и 
имеют место против тех сечений балки, где приложены соответственно сосредоточенные силы или изгибающие моменты. Величина скачка должна быть равна величине сосредоточенной силы или момента.
|
|
|
Лекция 9
9.1. Нормальные напряжения при “чистом изгибе”
В общем случае поперечного изгиб в сечениях балки, как это видно из разработанного выше примера, возникают поперечные силы и изгибающие моменты. Первым соответствуют касательные напряжения, вторым – нормальные.
Если имеется силовой участок балки, где поперечная сила равна нулю, а изгибающий момент постоянен, то изгиб называется чистым (рис. 9.1).
Рис. 9.1 К выводу формулы напряжений при чистом изгибе
Дата добавления: 2018-02-15; просмотров: 2264; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!