Объемное напряженное сопротивление

Обобщенный закон Гука

Дан элементарный куб, по граням которого действуют главные напряжения 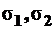 и . Необходимо найти относительные деформации куба 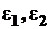 и , возникающие от действия трех пар главных напряжений (рис. 5.4).

 

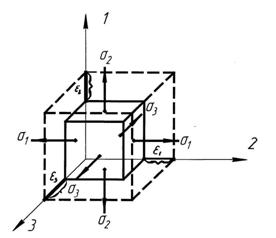
Рис. 5.4 Обобщенный закон Гука

 

При решении используется закон Гука в виде  и Пуассона -

В обозначении деформаций первый индекс обозначает направление деформации, второй – ее причину. Например,  – это относительная деформация по первому направлению от действия .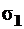

Рассмотрим деформацию по первому направлению от действия 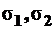 и , то есть :

от 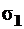 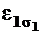   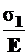                      =  - это продольная деформация от ;

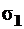от 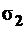 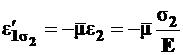           - это поперечная деформация от   ;

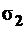от  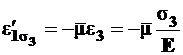          - это поперечная деформация от .

Таким образом:

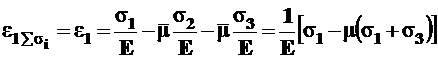                .      (5.4)

По аналогии можно получить

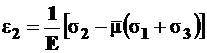                                       ,                            (5.5)

                                       .                           (5.6)

Три формулы – 5.4, 5.5 и 5.6 представляют собой обобщенный закон Гука.

Следует обратить внимание на то, что все три главных напряжения, показанные на рис. 5.3,являются растягивающими. Следовательно, если в условии задачи имеются сжимающие напряжения, то их следует подставлять в формулы 5.4…5.6 со знаком минус.

 

Энергия деформации при объемном напряженном состоянии

Для линейного напряженного состояния мы имели

              .                    (5.7)    

Для объемного напряженного состояния полная удельная потенциальная энергия будет равна

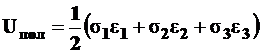                                  ,                  (5.8)

Подставляя значения 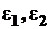 и   из обобщенного закона Гука, получим

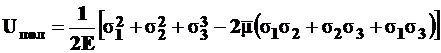               .    (5.9)

Полную потенциальную энергию делят на потенциальные энергии изменения объема и формы. Подсчитано, что удельная потенциальная энергия изменения объема равна

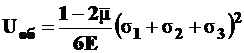                                   .                      (5.10)

Разность полной потенциальной энергии деформации и удельной потенциальной энергии изменения объема дает величину удельной потенциальной энергии изменения формы

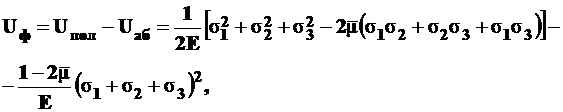
После упрощения имеем

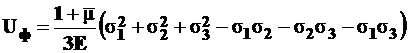                   .     (5.11)

Эта формула используется в одной из гипотез прочности (см. ниже формулы 16.11 и 16.12).

Лекция 6

Сдвиг. Закон Гука при чистом сдвиге 

Сдвигом называется такой вид напряженного и деформированного состояния, когда в поперечном сечении стержня возникает только перерезывающая (поперечная) сила.

Рассмотрим, например, призму (рис.6.1), в плоскости верхней грани которой действует сдвигающая нагрузка Т (главный вектор равномерно распределенной

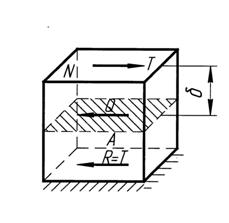Рис. 6.1 Возникновение пло                            площадки сдвига

сдвигающей нагрузки). Очевидно, что в любом сечении призмы, параллельном этой грани, будут действовать внутренние сдвигающие усилия с равнодействующей Q. Кроме этого, возникает пара сил с плечом 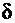, то есть сдвиг, как правило, сопровождается изгибом. При 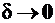 в сечении возникает только сдвигающая сила Q(например, резка ножницамибумаги). Это будет случай “чистого сдвига”. Если считать распределение внутренних усилий в сечении равномерным, то величина касательных напряжений будет равна

,

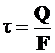а критерий прочности           .                                    (6.1)

На основе этой формулы производится расчет заклепочных и сварных соединений на срез по принципу

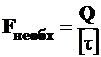                                            .                                           (6.2)

Если вырезать около произвольной точки А (рис. 6.1) элементарный кубик с гранями, параллельными граням призмы, то в соответствии с законом парности

касательных напряжений в случае чистого сдвига на них будут действовать

только касательные напряжения 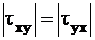 (рис. 6.2),  и .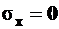

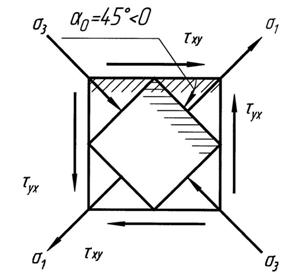
Рис. 6.2 Главные площадки при сдвиге

 

Зная величину напряжений, действующих на взаимно перпендикулярных площадках, можно по формуле (5.2) найти величины главных напряжений

,

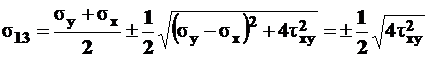так как ,           ,             ,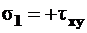

 

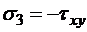и по (4.9) – положение главных площадок

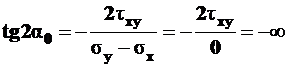                         , откуда     .

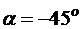Предположим теперь, что нижняя грань такого кубика защемлена (рис. 6.3), а длина всех ребер равна а. В этом случае под действием сдвигающих усилий произойдет его деформирование, показанное на рис. 6.3.

Величина Dа называется абсолютным сдвигом, .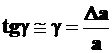

Здесь  - угол сдвига и в то же время величина относительного сдвига. Тогда

.                                     (1П)

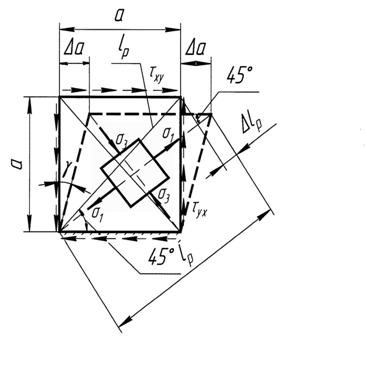
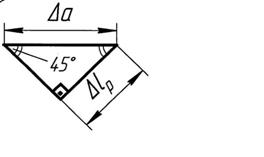
Рис. 6.3 К выводу закона Гука при сдвиге

 

С учетом малости деформаций (см. рис. 6.3) можно считать, что

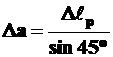                                                ,                                     (2П)

где - абсолютное удлинение растянутой диагонали квадрата со стороной а.

Из (1) и (2), приравнивая правые части формул, получим

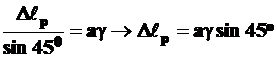                                .                     (3П)

Относительное удлинение растянутой диагонали равно 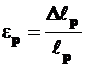, откуда  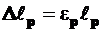и с учетом, что 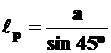, получим

                                             .                                  (4П)

Приравнивая правые части формул (3) и (4), имеем 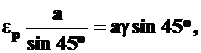 то есть  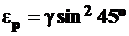и окончательно

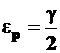                                                     .                                           (5П)

Используя обобщенный закон Гука, можно записать (5.4)

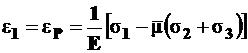, а с учетом значени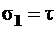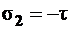й ,  и  (индексы у  можно опустить),

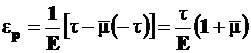                                  .                        (6П)

Приравнивая правые части формул (5) и (6), получим

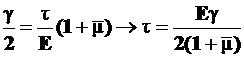                                   .                        (7П)

В формуле (7) постоянные величины могут быть обозначены через G

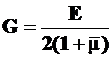                                                .                                     (6.3)

Это выражение называют модулем упругости второго рода или модулем сдвига - 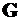. Так же, как и модуль Юнга Е, он имеет размерность напряжения. Подставляя (6.3) в (7П), получаем выражение закона Гука при сдвиге

.                                              (6.4)

То есть при малых упругих деформациях касательные напряжения пропорциональны относительному сдвигу.

---

Дата добавления: 2018-02-15; просмотров: 512; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!