Продольные и поперечные деформации.
Законы Р. Гука и С. Пуассона
Рассмотрим деформации стержня, представленного на рис. 2.2.
Рис. 2.2 Продольные и поперечные деформации при растяжении
Обозначим через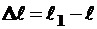 
абсолютное удлинение стержня. При растяжении – это положительная величина. Через 
– абсолютную поперечную деформацию. При растяжении – это отрицательная величина. Знаки 
и 
соответственно меняются при сжатии.
Отношения
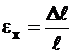(эпсилон) или 
, (2.2)
называют относительным удлинением. Оно положительно при растяжении.
Отношения
или 
, (2.3)
называют относительной поперечной деформацией. Она отрицательна при растяжении.
Р. Гук в 1660 г. открыл закон, который гласил: «Каково удлинение, такова сила». В современном написании закон Р. Гука записывается так:
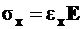, (2.4)
то есть напряжение пропорционально относительной деформации. Здесь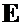 
– модуль упругости первого рода Э. Юнга – это физическая постоянная в пределах действия закона Р. Гука. Для различных материалов она различна. Например, для стали она равна 2·106 кгс/см2 (2·105 МПа), для дерева – 1·105 кгс/см2 (1·104 МПа), для резины – 100 кгс/см2 (10 МПа) и т.д.
Учитывая, что 
, а 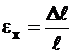, получим
, (2.5)
где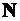 
– продольная сила на силовом участке;
|
|
|
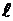– длина силового участка;
– жесткость при растяжении-сжатии.
То есть абсолютная деформация пропорциональна продольной силе, действующей на силовом участке, длине этого участка и обратно пропорциональна жесткости при растяжении-сжатии.
При подсчете по действию внешних нагрузок
, (2.6)
где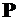 
– внешняя продольная сила;
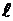– длина участка стержня, на котором она действует. В этом случае применяют принцип независимости действия сил*).
С. Пуассон доказал, что соотношение 
– есть постоянная величина, различная для различных материалов, то есть
или 
, (2.7)
где 
– коэффициент С. Пуассона. Это, вообще говоря, отрицательная величина. В справочниках ее значение дается «по модулю». Например, для стали она равна 0,25…0,33, для чугуна – 0,23…0,27, для резины – 0,5, для пробки – 0, то есть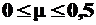 
. Однако для древесины он может быть и больше 0,5.
Экспериментальное исследование процессов деформации и
Разрушения растянутых и сжатых стержней
Русский ученый В.В. Кирпичев доказал, что деформации геометрически подобных образцов подобны, если подобно расположить действующие на них силы, и что по результатам испытаний небольшого образца можно судить о механических характеристиках материала. При этом, конечно, учитывается масштабный фактор, для чего вводится масштабный коэффициент, определяемый экспериментально.
|
|
|
Диаграмма растяжения малоуглеродистой стали
Испытания производят на машинах разрывного действия с одновременной записью диаграммы разрушения в координатах 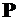– сила, – абсолютная деформация (рис. 2.3, а). Затем производят пересчет эксперимента с целью построения условной диаграммы в координатах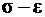 
(рис. 2.3, б).
По диаграмме (рис. 2.3, а) можно проследить следующее:
– до точки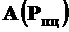 
справедлив закон Гука;
– от точки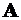 
до точки 
деформации остаются упругими, но закон Гука уже не справедлив;
– от точки 
до точки 
деформации растут без увеличения нагрузки. Здесь происходит разрушение цементного каркаса ферритовых зерен металла, и нагрузка передается на эти зерна. Появляются линии сдвига Чернова–Людерса (под углом 45° к оси образца);
– от точки 
до точки 
– стадия вторичного упрочнения металла. В точке 
нагрузка достигает максимума, и затем появляется сужение в ослабленном сечении образца – «шейка»;
|
|
|
– в точке 
– образец разрушается.
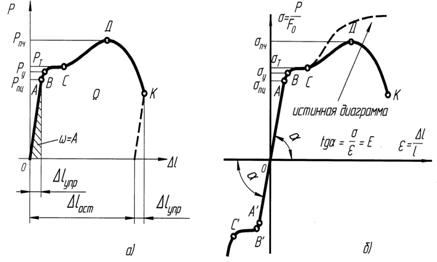
Рис. 2.3 Диаграммы разрушения стали при растяжении и сжатии
Диаграммы позволяют получить следующие основные механические характеристики стали:
– предел пропорциональности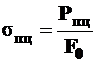 
– наибольшее напряжение, до которого справедлив закон Гука (2100…2200 кгс/см2 или 210…220 МПа);
– предел упругости 
– наибольшее напряжение, при котором деформации еще остаются упругими (2300 кгс/см2 или 230 МПа);
– предел текучести 
– напряжение, при котором деформации растут без увеличения нагрузки (2400 кгс/см2 или 240 МПа);
– предел прочности 
– напряжение, соответствующее наибольшей нагрузке, выдерживаемой образцом за время опыта (3800…4700 кгс/см2 или 380…470 МПа);
– остаточное относительное удлинение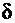 
(дельта)
при 
; 
;
– остаточное относительное сужение 
(пси)
;
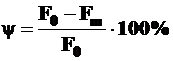
– модуль упругости Юнга 
(2×10 кгс/см6 или 2×105 МПа ).
В перечисленных формулах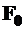 
– первоначальная площадь образца, 
– площадь шейки.
Некоторые пластические материалы не имеют на диаграмме площадки текучести (между точкой и точкой ). Для них назначается условный предел текучести, соответствующий остаточной деформации, равной 0,2 % – 
.
Для построения истинной диаграммы разрушения необходимо фактическую нагрузку 
в каждый момент времени 
делить на соответствующую фактическую площадь поперечного сечения 
:
|
|
|
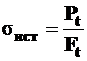. (2.8)
Дата добавления: 2018-02-15; просмотров: 859; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!