Диаграммы сжатия стали-3 и разрушения хрупких материалов
На рис. 2.3, б показана диаграмма сжатия образца длиной 
из малоуглеродистой стали. Точки 
и 
– соответствуют пределам пропорциональности и текучести, то есть практически
и 
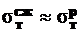, а 
.
Для хрупких материалов характерно отсутствие пластических деформаций. Для них определяется только один предел – предел прочности или временное сопротивление – 
. По тангенсу угла наклона прямого участка диаграммы подсчитывают модуль упругости – 
.
ЛЕКЦИЯ 3
Допускаемые напряжения. Расчеты на прочность
Допускаемые напряжения для пластических материалов назначаются по пределу текучести 
, который уменьшается на соответствующий коэффициент запаса 
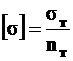. (3.1)
Для хрупких материалов назначаются два допускаемых напряжения:
при растяжении 
,
при сжатии 
, (3.2)
где 
и 
– пределы прочности при растяжении и сжатии, а 
– коэффициент запаса.
Решаются три вида задач расчета на прочность.
1. Подбор необходимой площади поперечного сечения 
при известных 
и 
и критерии прочности
, (3.3)
. (3.4)
2. Определение грузоподъемности стержня
. (3.5)
3. Проверка фактических напряжений - по формуле
. (3.6)
Допускается пятипроцентная перегрузка или недогрузка стержня.
|
|
|
Полная и удельная потенциальная энергия деформации
При растяжении
Рис. 3.1 К определению
потенциальной энергии деформации
|
Учитывается, что внешняя нагрузка прикладывается статически, то есть возрастает от нуля до конечной величины 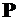 и, следовательно, переменна во времени, а также то, что работа равняется произведению силы на перемещение. Предположим (рис. 3.1), что в момент времени  нагрузка  получит приращение  , а уже имевшееся удлинение  – приращение  . Тогда элементарная работа будет равна
|
.
Согласно закону Гука,
.
, как величина второго порядка малости, а 
, поэтому также может быть приравнена нулю. В результате имеем
.
После интегрирования получим
. (3.7)
Отметим, что с учетом (2.6) можно записать полученное выражение в виде
. (3.8)
Следовательно, работа внешних сил может быть подсчитана по площади диаграммы разрушения образца при растяжении. Действительно, (рис. 2.3, а) в упругой области работы материала
. (3.9)
|
|
|
Если пренебречь побочными эффектами, то по принципу Ж. Лагранжа работа внешних сил равна потенциальной энергии деформации, накапливаемой образцом в процессе нагружения, поэтому
. (3.10)
Удельная потенциальная энергия равна
, (3.11)
где 
– объем образца.
Из формулы (3.10) видно, что одним из энергоемких материалов является резина с Е = 100 кгс/см2 » 10 МПа.
Работа, идущая на разрушение образца, также может быть подсчитана по площади диаграммы 
(рис. 2.3) с учетом масштаба ее записи.
Напряжения и деформации призматического стержня
Дата добавления: 2018-02-15; просмотров: 605; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!