Виды напряженных состояний в некоторой точке объема элемента
Для вычисления величин максимальных нормальных и касательных напряжений, знание которых необходимо для расчетов на прочность, необходимо изучить общие законы распределения напряжений в различных сечениях (площадках) напрягаемого тела (элемента конструкции, детали и т.д.).
Согласно теории упругости, вокруг любой точки тела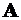 
можно выделить элементарный куб, по граням которого будут действовать только нормальные
напряжения, а касательные напряжения будут равны нулю (рис. 4.1).
Грани куба, на которых не возникают касательные напряжения, называются главными площадками, а сам куб – главным кубом.
Нормальные напряжения, действующие по граням куба, называются главными напряжениями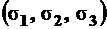 
.
По тому, сколько пар главных напряжений действует по граням главного куба, различают три вида напряженных состояний в точке тела: линейное (рис. 4.1, а), плоское (рис. 4.1, б) и объемное (рис. 4.1, в).
Рис. 4.1 Виды напряженных состояний
Принимается, что всегда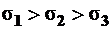 
, и учитывается их знак.
Линейное напряженное состояние
Ставится задача: найти величины напряжений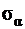 
и 
, действующих на наклонной площадке, проходящей через точку 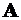и образующей с поперечным
сечением произвольный угол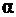 
>0 (рис. 4.2, а).
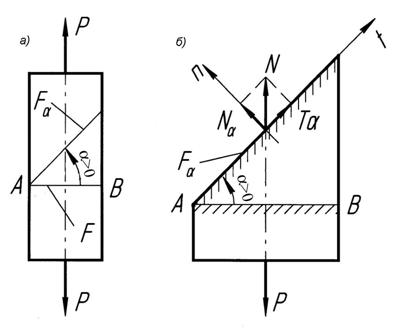
Рис. 4.2 К анализу линейного напряженного состояния
На площадке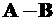 
– поперечном сечении – нормальные напряжения равны 
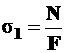(то, что это главные напряжения, будет доказано ниже).
|
|
|
На площадке, наклоненной под углом 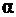(рис. 4.2, б), так как он отложен от заданной площадки 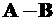против часовой стрелки, внутренние усилия равны
, 
, 
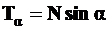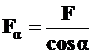. (4.1)
Напряжения на этой площадке будут равны
, (4.2)
. (4.3)
Интересно рассмотреть величину касательных напряжений, действующих на площадке, сопряженной с рассматриваемой,
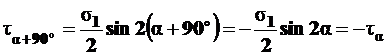, (4.4)
то есть на взаимно перпендикулярных площадках касательные напряжения равны по величине и обратны по знаку – это закон парности касательных напряжений (рис. 4.3, а).
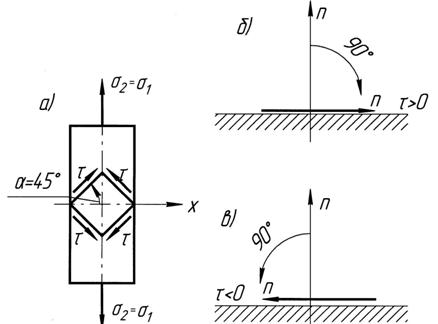
Рис. 4.3 Площадки сдвига и знаки касательных напряжений
Свойство взаимности (парности) касательных напряжений является общим свойством, справедливым при любом виде напряженного состояния.
Проанализируем выражение (4.2) -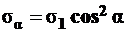 
, для чего продифференцируем его
. (4.5)
Значение первой производной отличается от выражения для (4.3) только множителем – 1/2, а так как 
, то экстремальные значения 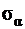будут на площадках, где 
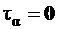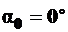и при 
и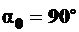 
, так как только в этом случае 
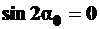, следовательно, это и есть главные площадки. Действительно, из формулы (4.2) следует, что
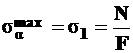при 
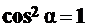, то есть при 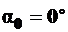– это поперечное сечение;
|
|
|
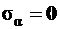при 
, то есть при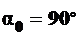 
– это продольные площадки;
на наклонных площадках –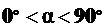 
нормальные напряжения меняются в пределе 
.
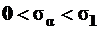Проанализируем формулу (4.3) -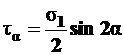 
.
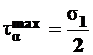при 
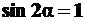, то есть при 
,
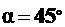при 
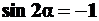, то есть при 
.
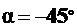Эти взаимно перпендикулярные площадки, на которых касательные напряжения достигают экстремальных значений, называются площадками сдвига. Далее 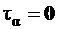при 
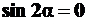, то есть при 
и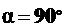 
.
Это есть поперечные и продольные площадки, которые являются, следовательно, главными, как уже было сказано выше.
Следует отметить, что касательные напряжения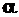 
будут считаться положительными если при повороте нормали n на 
ее направление совпадет с направлением этих напряжений (рис. 4.3 б и в).
Дата добавления: 2018-02-15; просмотров: 526; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!