Виды напряжений. Выражение внутренних сил
И моментов через напряжения
Главный вектор  и главный момент
и главный момент  реально не существуют. Они представляют собой лишь статический эквивалент элементарных внутренних сил, распределенных по площади сечения по различным законам. Эти силы характеризуются интенсивностью (рис. 1.4, а).
реально не существуют. Они представляют собой лишь статический эквивалент элементарных внутренних сил, распределенных по площади сечения по различным законам. Эти силы характеризуются интенсивностью (рис. 1.4, а).
 Рис. 1.4 Виды напряжений
Рис. 1.4 Виды напряжений
| 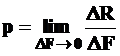 , (1.1) (1.1)
где , (1.1) (1.1)
где  – равнодействующая внутренних сил на весьма малой площади – равнодействующая внутренних сил на весьма малой площади  .
Равнодействующая .
Равнодействующая  может быть разложена на составляющую может быть разложена на составляющую  , действующую по перпендикуляру к сечению и составляющую , действующую по перпендикуляру к сечению и составляющую 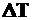 , действующую в плоскости сечения (рис. 1.4, а).
Интенсивность касательных сил в рассматриваемой точке сечения называется касательным напряжением и обозначается греческой буквой , действующую в плоскости сечения (рис. 1.4, а).
Интенсивность касательных сил в рассматриваемой точке сечения называется касательным напряжением и обозначается греческой буквой  (тау). (тау).
|
 . (1.2)
. (1.2)
Интенсивность нормальных сил – нормальным напряжением и обозначается греческой буквой  (сигма).
(сигма).
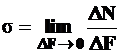 . (1.3)
. (1.3)
Размерности напряжений – кгс/см2 или МПа (мегапаскаль в системе СИ), 10 кгс/см2 @ 1 МПа. Они чаще всего встречаются в учебной и научной литературе.
Величина полного напряжения может быть определена по формуле
 . (1.4)
. (1.4)
Внутренние усилия и моменты могут быть выражены через напряжения 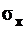 и
и  , действующие на элементарной площадке
, действующие на элементарной площадке  (рис. 1.4, б).
(рис. 1.4, б).
|
|
|
 ,
,  ,
,  ,
,
 . (1.5)
. (1.5)
 ,
,  .
.
ЛЕКЦИЯ 2
Растяжение, сжатие. Продольная сила, напряжение
Растяжением-сжатием называется такой вид напряженного и деформированного состояния, когда в поперечном сечении стержня возникает только продольная сила. Если продольная сила направлена по нормали от сечения, то она положительна и имеет место растяжение, если – по нормали к сечению, то она отрицательна и имеет место сжатие.
Продольная сила в сечении определяется с помощью метода сквозного разреза. Она численно равна алгебраической сумме внешних сил, действующих вдоль оси стержня по одну сторону от сечения, и противоположно направлена.
Для выяснения закона распределения продольных сил по длине стержня строится эпюра 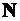 .
.
Здесь и далее эпюрой будет называться график, показывающий закон изменения какого-либо силового фактора по длине элемента конструкции.
Любая ордината эпюры показывает величину силового фактора в сечении, расположенном против данной ординаты.
Пример построения эпюры продольных сил дан на рис. 2.1.

Рис. 2.1 Пример построения эпюр продольных сил
|
|
|
Перед построением эпюры схему стержня разбивают на силовые участки – это части стержня от точки приложения одной внешней силы до точки приложения следующей внешней силы. Таких участков в рассматриваемом примере три.
Следует обратить внимание на то, что продольная сила в сечениях стержня определяется из суммы проекций всех сил, действующих на оставшуюся часть стержня, на ось х. Скачки на эпюре равны величинам внешних продольных сил, приложенных в соответствующих сечениях. Как показывает опыт, простое растяжение или сжатие характеризуются тем, что поперечные сечения стержня, плоские и нормальные к оси стержня до приложения внешней нагрузки, остаются плоскими и нормальными к этой оси и после приложения внешней нагрузки (гипотеза плоских сечений Я. Бернулли).
Это означает, что элементарные внутренние продольные силы 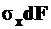 распределены по сечению
распределены по сечению  равномерно. Тогда, используя формулу (1.5), имеем
равномерно. Тогда, используя формулу (1.5), имеем
 или
или  . (2.1)
. (2.1)
В формуле (2.1) плюс и минус означают, соответственно, растяжение или сжатие.
Таким образом, напряжение в соответствующем сечении может быть вычислено по величине продольной силы. Максимальное напряжение в стержне вычисляется, соответственно, по максимальной абсолютной величине продольной силы. В примере, приведенном на рис. 2.1,  – это 11 кН. В дальнейшем она используется для расчета стержня на прочность.
– это 11 кН. В дальнейшем она используется для расчета стержня на прочность.
|
|
|
Дата добавления: 2018-02-15; просмотров: 519; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
