С учетом его собственной массы
Обозначим через 
объемную массу материала, тогда усилие в сечении на расстоянии 
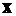от конца стержня будет равно
, (3.12)
где 
– площадь стержня (рис. 3.2).
Максимальное усилие будет равно
, (3.13)
Рис. 3.2 К определению напряжений
и деформаций с учетом собственного веса
| а максимальное напряжение
 . (3.14)
Условие прочности запишется в виде
 , (3.15)
а необходимая площадь стержня с учетом собственного веса
 . (3.16)
|
Если конструкция, например, фундамент колонны, состоит из ступенчатых призматических стержней одинаковой высоты и в основании каждой ступени напряжения равны допускаемым, то площадь любой n-ой ступени будет равна
. (3.17)
Если учесть, что по закону Гука 
, то с учетом собственной массы в сечении 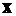и формулы (3.12)
. (3.18)
Но для элемента длиной 
(рис. 3.2) 
, откуда 
и, подставляя значения 
из формулы (3.18), получим
и после интегрирования
или
. (3.19)
Если внешняя нагрузка отсутствует, то
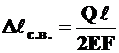. (3.20)
|
|
|
Расчет на жесткость при растяжении-сжатии заключается в ограничении деформаций стержня, то есть
, (3.21)
где 
– допускаемые деформации, которые оговариваются соответствующими ГОСТ или условием задачи.
Статически неопределимые системы при растяжении-сжатии
Статически неопределимыми называются такие системы, при расчете которых число неизвестных опорных реакций (число связей) превышает число уравнений статики, которые можно записать для данной системы.
Заметим, что связью называется препятствие, не допускающее изменения взаимного положения точек или сечений системы.
Метод сил в применении к статически неопределимым задачам
Растяжения-сжатия
Последовательность решения задач этим методом такова:
1. Составляем уравнения статики для «заданной системы» (рис. 3.3, а)
. (3.22)
Степень статической неопределимости равна 
.
2. Отбрасываем «лишнюю» связь (или связи) и вместе с ней всю заданную нагрузку – получаем «основную систему», которая по геометрическим размерам аналогична заданной системе (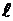 
, h, b и т.д. равны), но статически определима (рис. 3.3, б, в).
|
|
|
3. Загружаем «основную систему» заданной нагрузкой и получаем грузовую систему (рис. 3.3, г), используя принцип независимости действия сил, «лишней» неизвестной 
(рис. 3.3, д), приложенной по направлению отброшенной связи. Их совокупность должна обеспечить эквивалентность ее заданной.
Эквивалентная система
Рис. 3.3 К расчету статически неопределимых систем
Действительно, полученная система под действием силы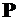 
будет деформироваться на величину 
(перемещение сечения 
под действием силы 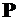). Однако в заданной системе сечение было неподвижно, поэтому роль силы 
– вернуть сечение в исходное положение, то есть переместить на величину 
(перемещение сечения под действием силы ), то есть должно быть выполнено условие
. (3.23)
Это добавочное условие ограничивает деформации основной системы и выражает условие совместимости деформаций заданной статически неопределимой системы.
4. Используя закон Гука, получим
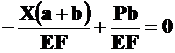. (3.24)
|
|
|
Это уравнение деформаций. В результате его решения совместно с уравнением (3.22) и, учитывая, что 
, получим значения реакций 
и 
.
ЛЕКЦИЯ 4
Дата добавления: 2018-02-15; просмотров: 455; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!