Расчеты на прочность при кручении
Как следует из формулы (7.1), максимальные касательные напряжения 
будут при значении 
(рис. 7.1,б). Критерий прочности при кручении имеет вид
, (7.2)
где 
- геометрическая характеристика сечения, носящая название полярного момента сопротивления и имеющая размерность длины в третьей степени;
- максимальный крутящий момент, берущийся из эпюры, например,
(3,0 кН×мна рис. 6.4), 
- допускаемые напряжения при кручении.
Подбор поперечного сечения можно осуществить по формуле
. (7.3)
Однако для практического использования формул (7.1) и (7.3) необходимо выразить 
и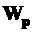 
через диаметрстержня D.
Рассмотрим стержень диаметром D (рис. 7.2).
Рис.7.2 К расчету величины
полярного момента инерции
| Площадь элементарной площадки  равна  , 
то есть
 . (7.4)
|
откуда
(7.5)
Значение 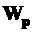позволяет подобрать диаметр вала. Подставим (7.5) в (7.3)
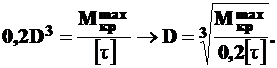(7.6)
Угол закручивания. Расчет на жесткость при кручении
Мы имели два значения постоянной с
и 
, то есть можно приравнять правые части этих формул
.
Если и постоянны, то
(7.7)
Угол закручивания пропорционален крутящему моменту, длине участка, на котором он действует, и обратно пропорционален произведению GIр, которое называется жесткостью при кручении.
|
|
|
Таким образом, расчет на жесткость при кручении можно представить в виде
. (7.8)
Обычно расчет проводят на длину вала в 100 см, а угол закручивания выражают в градусах
. (7.9)
При расчете валов 
на 100 см длины вала принимают: при обычных статических нагрузка -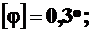 
при переменных напряжениях - 
при ударных нагрузка - 
Расчет полого вала
Задаются отношением 
откуда 
, (рис. 7.3)
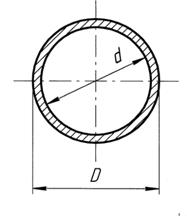
Рис. 7.3 К расчету полого вала
, (7.10)
Диаметр полого вала может быть найден по формуле
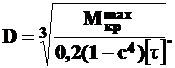. (7.11)
Потенциальная энергия при кручении
Если стержень, имеющий длину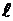 
и диаметр d, статически закручивается моментом на угол 
, то так же как при растяжении-сжатии,
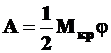(7.12)
или
(7.13)
|
|
|
При переменныхМкр или Iр
(7.14)
Лекция 8
Плоский изгиб. Виды внешних нагрузок и опор балок,
Определение реакций опор
Изгибом называется такой вид напряженного и деформированного состояния, когда в поперечных сечениях стержня, называемого балкой, возникают изгибающие моменты, действующие в плоскости, перпендикулярной поперечному сечению, и поперечные силы, действующие в этом сечении. Такой вид изгиба называется поперечным.
Внешней нагрузкой при изгибе могут быть сосредоточены силы и изгибающие моменты, а также распределенные нагрузки. Последние, как правило, обозначаются через q и имеют размерность тс/м, кН/м и т.п.
Внешнюю нагрузку уравновешивают опорные реакции, возникающие в опорах балок. Вид опоры реакций зависит от устройства опоры, то есть от того, сколько связей накладывает это устройство.
Подвижная шарнирная опора (рис.8.1,а) накладывает одну связь, препятствующую перемещениям в направлении, перпендикулярном ее основанию.
Рис. 8.1 Виды опор и реакций в них
Этой связи соответствует одна реакция V.Неподвижная шарнирная опора (рис.8.1, б) накладывает две связи, препятствующие перемещениям в вертикальной и горизонтальной плоскостях. Им соответствует две реакции – V и Н.
|
|
|
Консольная заделка (защемление) накладывает три связи, препятствующие вертикальному и горизонтальному перемещениям и повороту опоры (рис. 8.1, в).
В статически определимых балках опоры устраиваются таким образом, чтобы было наложено три связи, причем должна отсутствовать возможность перехода системы в механизм или мгновенная ее изменяемость (см. разделы теоретической механики, посвященные этому вопросу).
Рекомендуется следующая последовательность при вычислении опорных реакций:
1. Пишут уравнения суммы моментов всех внешних сил относительно центров тяжести опорных сечений и приравнивают их к нулю. Из этих уравнений определяют две неизвестные опорные реакции.
2. Из суммы проекций всех внешних сил на ось x находят третью неизвестную реакцию.
3. Проверяют правильность определения вертикальных опорных реакций с помощью уравнения суммы проекций всех сил на ось у, которая должна бать равна нулю.
Внутренние усилия при изгибе
После определения опорных реакций приступают к исследованию напряженного состояния в сечениях балки, для чего должны быть найдены внутренние силовые факторы – поперечные силы и изгибающие моменты. Они снова определяются с помощью метода сквозного разреза.
|
|
|
Дата добавления: 2018-02-15; просмотров: 565; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!