Расчет на прочность при изгибе
Формула нормальных напряжений при чистом изгибе (9.1) с определенным приближением применяется для инженерных расчетов и в общем случае поперечного изгиба, когда высота балки значительно меньше ее длины. Максимальные напряжения в сечении балки будут, очевидно, в наиболее удаленных волокнах, то есть
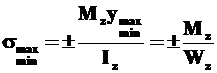 , (10.1)
, (10.1)
где  , (10.2)
, (10.2)
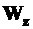 – момент сопротивления поперечного сечения относительно оси z – это геометрическая характеристика сечения, имеющая также, как
– момент сопротивления поперечного сечения относительно оси z – это геометрическая характеристика сечения, имеющая также, как  , размерность длины в третьей степени. Критерий прочности при изгибе имеет вид
, размерность длины в третьей степени. Критерий прочности при изгибе имеет вид
 ,
,  . (10.3)
. (10.3)
В этой формуле  - максимальное значение изгибающего момента (максимальная по абсолютной величине ордината, взятая из эпюры). Например, в примере на рис.8.5 – это 6.25 кН×м.
- максимальное значение изгибающего момента (максимальная по абсолютной величине ордината, взятая из эпюры). Например, в примере на рис.8.5 – это 6.25 кН×м.
 - наибольшее растягивающее или сжимающее напряжение;
- наибольшее растягивающее или сжимающее напряжение;
 - допускаемые напряжения при растяжении или сжатии.
- допускаемые напряжения при растяжении или сжатии.
Из критерия прочности может быть получена формула для подбора поперечного сечения балки
 . (10.4)
. (10.4)
Можно рекомендовать следующий порядок проверочного расчета на прочность при изгибе:
1. Строим эпюры поперечных сил и моментов и находим наибольшую по абсолютной величине ординату из эпюры  .
.
|
|
|
2. Находим центр тяжести сечения для того, чтобы знать положение нейтральной оси z.
3. Вычисляем (если это необходимо) момент инерции сечения  относительной нейтральной оси.
относительной нейтральной оси.
4. Вычисляем момент сопротивления сечения 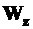 , найдя
, найдя  - расстояние до наиболее удаленного волокна по формуле
- расстояние до наиболее удаленного волокна по формуле
 .
.
5. Подсчитываем фактические максимальные напряжения по формуле (10.3) и сравниваем их с допускаемыми

 . (10.5)
. (10.5)
Если необходимо подобрать сечение балки, то используем формулу (10.4). Для прокатных профилей по таблицам ГОСТ можно подобрать близкое значение момента сопротивления  . Затем необходимо снова проверить фактическую величину нормальных напряжений
. Затем необходимо снова проверить фактическую величину нормальных напряжений

 . (10.6)
. (10.6)
Для прямоугольного и круглого профиля поперечного сечения необходимо знать их значения  и
и  .
.
Прямоугольное сечение.
Рассмотрим сечение, имеющее высоту h и ширину b (рис. 10.1,а)

Рис. 10.1 К выводу формул моментов инерции и сопротивления.
Подсчитаем значение осевого момента инерции поперечного сечения
 . (10.7)
. (10.7)
Относительно оси yон будет равен, соответственно,
 . (10.8)
. (10.8)
Значения сопротивления моментов будут равны
|
|
|
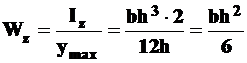 , (10.9)
, (10.9)
и  . (10.10)
. (10.10)
Круглое сечение. Рассмотрим сечение диаметром D(рис. 10.1,б). Значения осевых моментов инерции могут бать подсчитаны так
 или
или
 , так как оси zи y равноценны. Тогда
, так как оси zи y равноценны. Тогда
 и
и 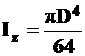 , а
, а  . (10.11)
. (10.11)
Диаметр балки круглого поперечного сечения может быть подобран так
 , а
, а  , откуда, приравнивая правые части формул, получим
, откуда, приравнивая правые части формул, получим
 . (10.12)
. (10.12)
Аналогично могут быть подобраны размеры балки прямоугольного поперечного сечения, если задаться отношением его высоты и ширины.
Дата добавления: 2018-02-15; просмотров: 478; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
