Работа единичной силы (или момента) на перемещении от заданной нагрузки равна работе внутренних сил от заданной нагрузки на перемещении, вызванной единичной силой (или моментом).
Можно принять следующий порядок вычислений перемещений по методу Мора:
- определяем опорные реакции системы от внешней нагрузки, разбиваем ее на силовые участки пишем уравнения изгибающих моментов для этих участков;
- освобождаем систему от внешней нагрузки и прикладываем силу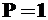 
в той точке, где мы хотим найти прогиб или линейное перемещение, или же момент 
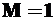в том сечении, угол поворота которого необходимо определить;
- находим опорные реакции системы от единичной нагрузки, разбиваем ее на силовые участки, аналогичные силовым участкам от внешней нагрузки, и пишем уравнения изгибающих моментов для этих участков. Отсчеты абсцисс всех участков в единичной и заданной системах необходимо производить от аналогичных начал координат, так как уравнения 
и 
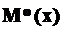должны иметь одни и те же пределы интегрирования;
- подставляем уравнения изгибающих моментов от внешней и единичной нагрузок в интеграл Мора (без учета членов, содержащих 
и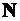 
) и вычисляем искомое перемещение.
Надо отметить, что положительное значение перемещения будет получаться в том случае, если его направление будет совпадать с направлением единичной силы или единичного момента.
Рассмотрим примеры применения метода Мора.
Пример 1. Нужно найти прогиб и угол поворота в любой точке балки, например,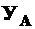 
и 
(рис. 13.1, а).
В консольной балке опорные реакции можно не находить, так как отсчет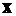 
начнем от т.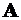 
|
|
|
(рис. 13.1, а).
Для нахождения прогиба освободим балку от нагрузки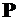 
и приложим в т. 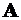силу .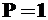
(рис. 13.1,б)
Подставляем и 
в интеграл Мора
.
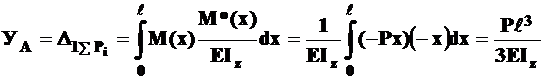Для нахождения угла поворота сечения 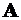приложим в нем 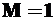(рис. 13.1, в).
В этом случае
.
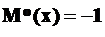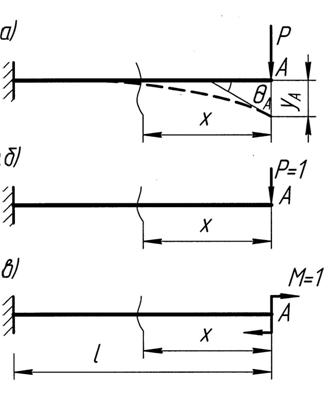
Рис. 13.1 К примерам расчета перемещений методом Мора
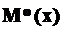Подставляем выражение и в интеграл Мора
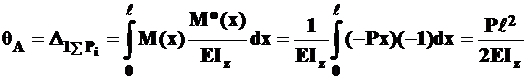
Пример 2. Определим угол поворота сечения в опоре (рис. 13.2 а). Реакции опор равны Р/2 .
Рис. 13.2 К примеру расчета перемещений методом Мора
.
Освобождаем балку от нагрузки, прикладываем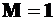 
в опоре 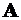и находим опорные реакции от этого момента. Они равны 
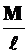(рис. 13.2 б).
Для построения эпюр моментов для схемы (13.2, б) можно было бы ограничиться одним силовым участком с границами от 0 до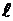 
, так как в грузовой системе силовых участков два, то необходимо искусственно сделать два силовых участка и в единичной системе с границами от 0до 
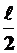, как это показано на рис. 13.2 б. Тогда
Находим угол поворота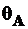 
с помощью интеграла Мора
.
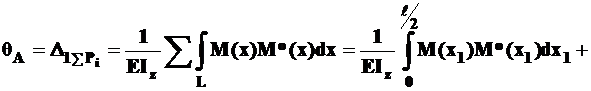
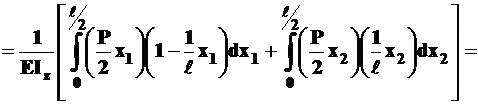
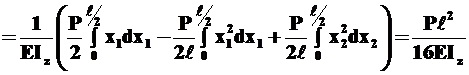Перемещения в примерах №1 и №2 получились положительными, так как их направления совпали с направлениями силы Р = 1 и момента .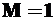
Метод вычисления перемещений А.К. Верещагина
Если хотя бы один из подинтегральных моментов в формуле Мора выражается уравнением первой степени, то есть эпюра, построенная по этому уравнению, ограничивается прямой линией, а жесткость балки постоянна, то применимо преобразование интеграла Мора, предложенное А.К. Верещагиным.
|
|
|
Преобразование можно провести в следующем порядке:
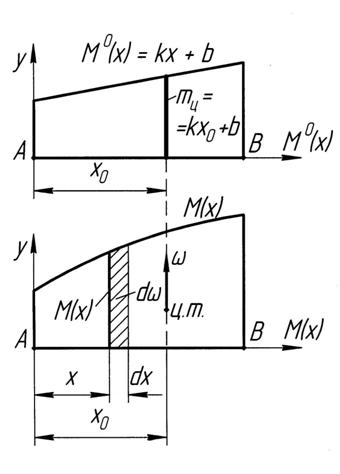
Рис. 13.3 К выводу формулы Верещагина
1. Пусть на участке 
стержня эпюра 
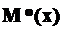прямолинейна и выражается уравнением (рис. 13.3)
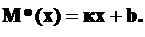(1П)
Вторая эпюра имеет произвольное очертание, определяемое уравнением .
2. Подставим выражение 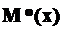в интеграл Мора
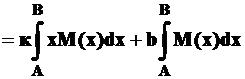. (2П)
Здесь второй интеграл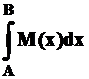 
выражает площадь эпюры в пределах от 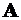до 
, которую можно обозначить через 
.
Первый интеграл выражает статический момент площади относительно оси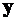 
.
Действительно:
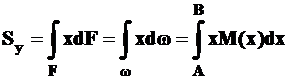, то есть 
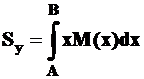. (3П)
В то же время, если 
-абсцисса центра тяжести площади эпюры 
, то статистический момент ее относительно оси 
равен
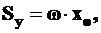(4П)
поэтому, приравнивая правые части (3П) и (4П), получим
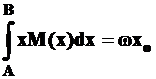. (5П)
Следовательно, интеграл Мора можно представить в виде
. (6П)
|
|
|
Но, так как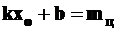 
- есть ордината из прямолинейной эпюры , фиксируемой абсциссой 
, то есть она расположена против центра тяжести эпюры , ограниченной кривой. Таким образом, интеграл Мора равен произведению этой площади на ординату прямолинейной эпюры 
, расположенную против центра тяжести этой площади эпюры моментов от внешних нагрузок. Окончательно получаем
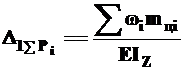. (13.2)
Это и есть формула Верещагина для вычисления линейных и угловых перемещений.
При применении метода Верещагина умение строить эпюры изгибающих моментов приобретает важнейшее значение, причем надо четко понимать, что он применим только на участках, где одна из эпюр прямолинейна. Если эпюра 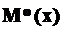имеет ломанное очертание, то необходимо “перемножать” эпюры порознь для каждого участка, ограниченного прямой линией, и результаты складывать. Надо помнить также, что ордината берется только из эпюры, ограниченной прямой линией.
Перемещение будет положительным, если обе эпюры будут располагаться по одну сторону от оси абсцисс.
Для вычислений по методу Верещагина требуется знать выражение площадей и координату центра тяжести тех фигур, которые чаще всего встречаются в эпюрах моментов.
|
|
|
Порядок вычисления перемещений по методу Верещагина вначале совпадает с порядком, применяемым в методе Мора, но после написания уравнений изгибающих моментов и 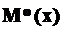по всем силовым участкам системы необходимо построить эпюры этих моментов. Затем эпюру 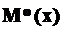разбивают на участки, ограниченные прямой линией, подсчитывают площади эпюры в границах этих участков и определяют положение их центров тяжести.
Далее, как правило, из подобия треугольников, определяют значения против соответствующих центров тяжести и, перемножая по участкам и , складывают полученные результаты. В результате после деления на жесткость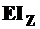 
находят значения искомых перемещений.
Рассмотрим примеры применения метода Верещагина.
Пример 1.
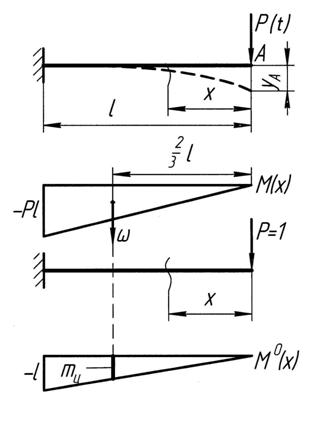Рис. 13.4 К примеру определения
прогиба методом Верещагина
| Снова найдем прогиб в точке 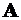консоли, так как этот пример служит своеобразным подтверждением правильности предлагаемых методов (рис. 13.4).
  ,
  ,
|
.
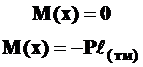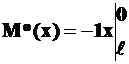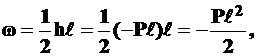
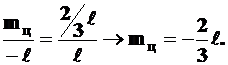
То есть прогиб получился тот же, что и при применении ранее разобранных методов.
Пример 2. Необходимо определить угол поворота сечения 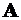- 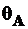(рис. 13.5).
.
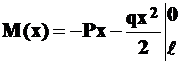
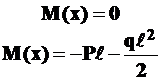В этом примере уравнение изгибающих моментов состоит из двух слагаемых, поэтому для точного подсчета значений перемещения рекомендуется построить две эпюры от каждой внешней нагрузки в отдельности, то есть применить принцип независимости действия сил.
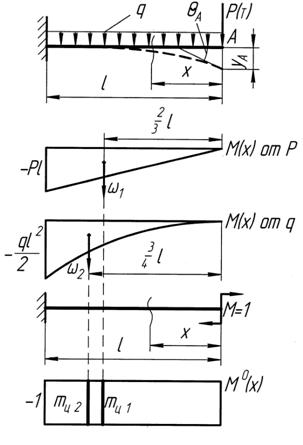Рис. 13.5 Пример определения угла
поворота методом Верещагина
|
|
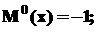
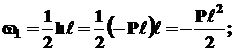
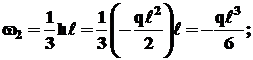
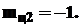
В заключение отметим, что основное достоинство метода Верещагина заключается в том, что можно обойтись без интегрирования произведений уравнений моментов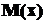 
и 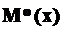, заменяя эту трудоемкую операцию простейшими геометрическими вычислениями. При его использовании в сложных случаях можно легко применять ЭВМ.
Лекция 14
Сложное сопротивление
Напомним, что сложным сопротивлением называются такие виды напряженного деформированного состояния элемента (стержня), при которых в его поперечных сечениях действует не менее двух компонентов внутренних усилий (силы и моменты).
Различные частные случаи сложного сопротивления можно разделить на такие, при которых в опасных точках поперечного сечения напряженное состояние является линейным (касательными напряжениями пренебрегают) – это косой изгиб и внецентренное растяжение-сжатие; или плоским – это изгиб с кручением, совместное действие растяжения (сжатия) и кручения. В первом случае расчет ведется по допускаемым напряжениям без применения теорий прочности (см. ниже), во втором – с применением теорий прочности.
Вся теория расчета элементов конструкций, находящихся в сложном напряженном состоянии, базируется на принципе независимости действия сил, согласно которому можно геометрически суммировать напряжения и перемещения, соответствующие различным видам деформаций.
Дата добавления: 2018-02-15; просмотров: 377; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!