Косой изгиб. Нормальные напряжения, расчет на прочность
Косой изгиб стержня возникает под действием нагрузок, плоскость действия которых (силовая плоскость) не совпадает ни с одной из главных центральных плоскостей инерции сечения).*)
При этом виде косого изгиба упругая линия стержня – плоская кривая, не лежащая в силовой плоскости.
Косой изгиб может быть пространственным. В этом случае нагрузки, вызывающие изгиб стержня, действуют в различных плоскостях, а упругая линия – пространственная кривая.
Рассмотрим консоль, нагруженную в плоскости ее торцевого сечения силой  . Направление действия этой силы (или плоскость ее действия) составляет с главной центральной осью инерции сечения -
. Направление действия этой силы (или плоскость ее действия) составляет с главной центральной осью инерции сечения -  (или главной плоскостью инерции) угол
(или главной плоскостью инерции) угол 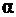 (рис. 14.1).
(рис. 14.1).
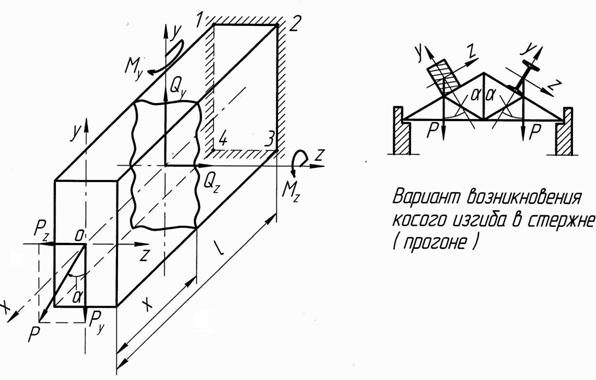
Рис. 14.1 Варианты возникновения косого изгиба в стержне (прогоне)
 *) Главной плоскостью инерции называется плоскость, проходящая через продольную ось прямого стержня и одну из главных центральных осей инерции поперечного сечения.
*) Главной плоскостью инерции называется плоскость, проходящая через продольную ось прямого стержня и одну из главных центральных осей инерции поперечного сечения.
Вывод формулы нормальных напряжений при косом изгибе можно вывести в следующем порядке:
1. Спроектируем силу 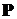 на оси
на оси 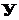 и
и 
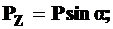
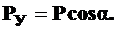 (14.1)
(14.1)
Под действием этих сил возникает как бы два простых поперечных изгиба в плоскостях 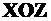 от (
от ( 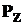 ) и
) и 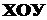 от (
от (  ).
).
То есть косой изгиб можно рассматривать как совокупность двух “прямых” поперечных изгибов во взаимно перпендикулярных плоскостях.
Воспользуемся методом сквозного разреза. В сечении, находящемся на расстоянии 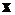 от конца консоли, возникнут четыре силовых фактора: две поперечные силы -
от конца консоли, возникнут четыре силовых фактора: две поперечные силы - 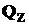 и
и  и два изгибающих момента -
и два изгибающих момента - 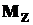 и
и 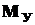 . Они будут равны
. Они будут равны

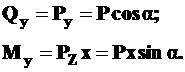 (14.2)
(14.2)
В случае чистого изгиба, когда 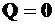 , и для изотропных материалов, когда влиянием поперечных сил можно пренебречь, расчет на прочность при косом изгибе ведут только по нормальным напряжениям, возникающим от изгибающих моментов
, и для изотропных материалов, когда влиянием поперечных сил можно пренебречь, расчет на прочность при косом изгибе ведут только по нормальным напряжениям, возникающим от изгибающих моментов 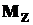 и
и 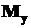 .
.
Таким образом, нормальное напряжение в произвольной точке поперечного сечения стержня, который подвержен косому изгибу, определяется на основе принципа независимости действия сил как алгебраическая сумма нормальных напряжений  и
и 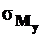 , каждое из которых обусловлено одним из прямых поперечных изгибов
, каждое из которых обусловлено одним из прямых поперечных изгибов
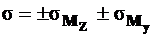 (14.3)
(14.3)
или
 . (14.4)
. (14.4)
Знак перед слагаемыми правой части уравнений (14.3) и (14.4) определяется по характеру изгиба (растяжение или сжатие). Кроме этого, следует отметить, что нейтральная ось при косом изгибе проходит через центр тяжести сечения, так как это следует из уравнения (14.4), при 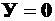 и
и 
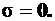
Максимальные нормальные напряжения в опасной точке поперечного сечения, не обладающего осями симметрии, буду равны
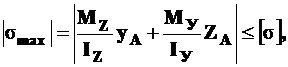 (14.5)
(14.5)
где 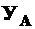 и
и 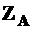 - координаты опасной точки сечения. При расчете на прочность они не должны превышать допускаемых.
- координаты опасной точки сечения. При расчете на прочность они не должны превышать допускаемых.
Критерий прочности для сечения, обладающего такими осями
 . (14.6)
. (14.6)
В формулы (14.5) и (14.6) необходимо подставлять максимальные значения 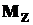 и
и 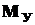 в опасном сечении стержня, которое определяется после построения соответствующих эпюр.
в опасном сечении стержня, которое определяется после построения соответствующих эпюр.
Для элементов конструкций из хрупких материалов следует производить две проверки
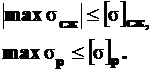 (14.7)
(14.7)
Подбор поперечного сечения при косом изгибе рекомендуется производить в следующем порядке :
- по одному из изгибающих моментов, имеющих в опасном сечении максимальную величину, находят, например,
 . (14.8)
. (14.8)
- по сортаментам прокатных профилей подбирают близкий по значению 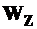 профиль, имеющий
профиль, имеющий 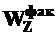 >
> 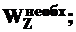
- проверяют фактическое значение нормальных напряжений, которые не должны превышать допускаемые по формуле
 . (14.9)
. (14.9)
Дата добавления: 2018-02-15; просмотров: 1113; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
