Кручение. Построение эпюр крутящих моментов
Кручением называется такой вид напряженного и деформированного состояния, когда в круглом поперечном сечении стержня (вал) возникают только внутренние крутящие моменты, действующие в плоскости сечения.
Крутящий момент, действующий в каком-либо сечении на левую часть стержня, равен и противоположно направлен крутящему моменту, действующему в том же сечении на его правую часть.Таким образом, кручение является примером чистого сдвига, при котором в поперечном сечении возникают только касательные напряжения (вывод не распространяется на стержни, которые являются статистически неопределенными).
При построении эпюр крутящих моментов, как и при растяжении-сжатии, используется метод сквозного разреза, то есть крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону отсечения.
Крутящий момент будет считаться положительным, если внешний скручивающий момент поворачивает круглый вал по часовой стрелке, если смотреть со стороны разреза. Правило остается в силе вне зависимости от того, равновесие какой части вала – левой или правой – будет рассматриваться. Пример построения эпюр Мкр показан на рис. 6.4.
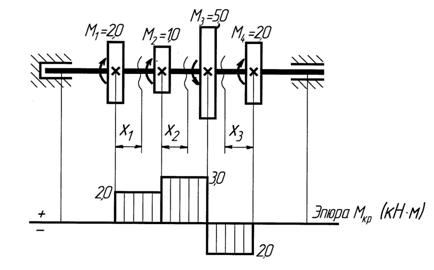
Рис. 6.4 Построение эпюры крутящих моментов
Мкр=М1=200 кгс×м, (2,0кН×м),
Мкр2= М1+ М2=300кгс×м, (3,0кН×м),
Мкр3=-М4=-200кгс×м, (-2,0кН×м),
При построении эпюр следует учитывать следующее: крутящие моменты в опорных сечениях равны нулю, если опоры – подшипники; скачки на эпюре крутящих моментов равны величине скручивающих моментов, приложенных в сечениях вала; в расчеты на прочность берется наибольшая по абсолютной величине ордината из эпюры крутящих моментов. В рассмотренном примере это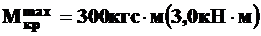 
.
|
|
|
Численную величину внешних моментов обычно определяют по числу оборотов вала и по мощности, передаваемой шкивами, по формулам
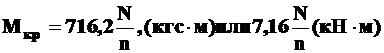, (6.5)
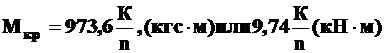, (6.6)
где N – мощность в л. с.;
n– число оборотов в минуту;
К– мощность в кВт.
ЛЕКЦИЯ 7
Напряжение при кручении стержня
Круглого поперечного сечения
При выводе формулы используются допущения:
1. При кручении стержня его поперечные сечения остаются плоскими и параллельными и лишь взаимно поворачиваются вокруг оси стержня.
2. Радиусы в плоскостях сечений поворачиваются, оставаясь плоскими.
Вывод имеет следующую последовательность (рис. 7.1):
1. Назовем продольную ось x, проходящую через центры тяжестей сечений стержня, полярной осью, а центры тяжестей - полюсами.
2. Вырежем из стержня цилиндрический отрезок длиной 
и произвольным радиусом 
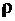. Его образующую обозначим через 1-2 (рис. 7.1, а).
|
|
|
Поскольку выделение этого цилиндрического отрезка условно, то, находясь в составе целого стержня, после приложения внешнего скручивающего момента Мкр, радиус 0-1 повернется на угол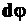 
и займет положение 1-1'.
Угол 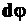называется углом закручивания на отрезке длиной . Он зависит от длины этого отрезка.
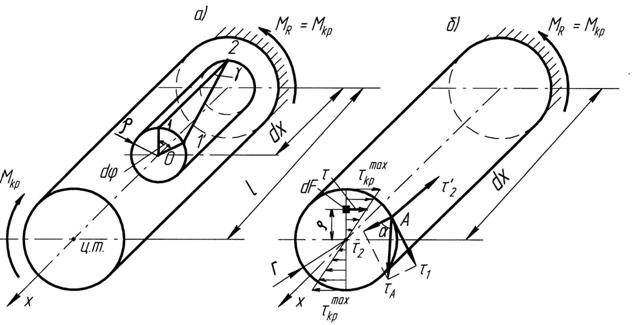
Рис.7.1 К выводу формулы касательных напряжений при кручении
Образующая 1-2 займет положение 2-1', повернувшись на угол 
- угол сдвига, не зависящий от длины.
3. Установим зависимость между углам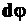и и , для чего можно подсчитать длину дуги 1 
1¢ через величину этих углов 1 1¢ 
(1П) и 1 1¢ 
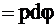(2П).
Приравнивая правые части формул (1) и (2), получим 
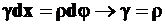
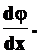(3П)
В формуле (3П) отношение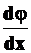 
- постоянная величина. Из нее следует, что угол сдвига пропорционален радиусу.
3. Поскольку выше говорилось, что кручение является примером чистого сдвига, то может быть применен закон Гука при сдвиге
, откуда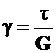 
(4П)
Приравнивая правые части формул (3) и (4), получим
.
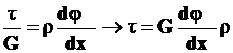Так как произведение G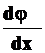 
- постоянная величина, то ее можно обозначить через с.
|
|
|
Тогда 
(5П)
Из формулы (5П) еще нельзя найти касательные напряжения, возникающие в поперечных сечениях круглого стержня при кручении, так как неизвестен своеобразный масштабный коэффициент с, а также ориентация этих напряжений по отношению к радиусу.
Вместе с тем, из формулы (5П) можно сделать важный вывод: под действием крутящего момента в любой точке круглого поперечного сечения стержня возникает касательное напряжение, величина которого пропорциональна расстоянию от полюса до рассматриваемой точки, то есть r.
4. Выясним, как ориентированы касательные напряжения по отношению к радиусу.
Предположим, что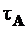 
(см. рис.7.1,б) образует с радиусом угол 
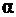, тогда оно может быть разложено на 
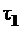,действующее по перпендикуляру к радиусу, и на 
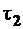, действующее по радиусу. Но если есть напряжение 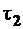, то по закону парности касательных напряжений на поверхности стержня вдоль его образующей должно действовать напряжение 
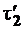, равное 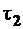по абсолютной величине. Однако эксперименты показывают, что поверхность стержня свободна от напряжений, то есть 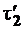=0 и, следовательно, 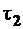также равно нулю.
Вывод: касательные напряжения в сечении круглого стержня, подвергающегося кручению, направлены по перпендикуляру к радиусу,то есть 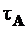совпадает с 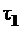(см. рис.7.1,б).
|
|
|
5. Рассмотрим теперь условие равновесия части стержня длиной .
На элементарной площадке 
будет действовать элементарная касательная сила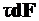 
. Момент этой силы относительно полюса будет равен
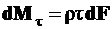
Полный момент внутренних касательных сил будет равен
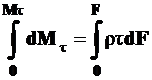или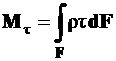 
Условие равновесия будет иметь вид
, 
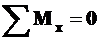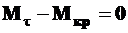или
(6П)
Подставляя в формулу (6П) значения t из (5П), получим
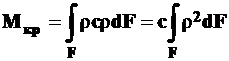(7П)
Интеграл вида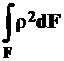 
не имеет физического смысла, зависит от радиуса конкретного сечения и имеет размерность длины в четвертой степени. Его называют полярным моментом инерции сечения и обозначают 
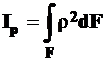. (8П)
Таким образом, подставляя значения (8) в (7), получим
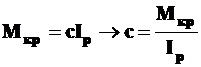, (9П)
Теперь можно значение постоянной сподставить в формулу (5)
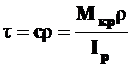и окончательно
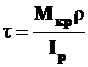. (7.1)
Это и есть формула для вычисления величины касательных напряжения в любой точке круглого поперечного сечения стержня, отстоящей от полюса на радиус .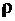
Дата добавления: 2018-02-15; просмотров: 3249; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!