Плоское напряженное состояние
Ставится задача: найти величины напряжений 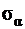 и
и  , действующих на наклонной площадке, если известны напряжения
, действующих на наклонной площадке, если известны напряжения 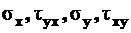 на сопряженных гранях элементарного куба (рис. 4.4, а).
на сопряженных гранях элементарного куба (рис. 4.4, а).
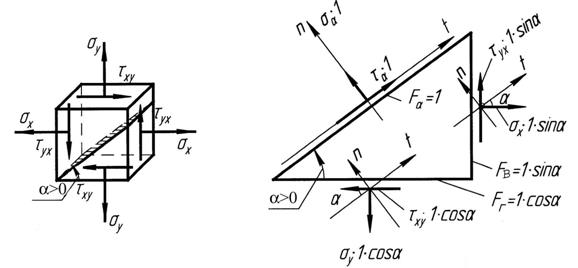
Рис. 4.4 К анализу плоского напряженного состояния
Мысленно отбросим верхнюю часть куба, сделав разрез по площадке, наклоненной к его основанию под углом 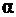 . Предположив, что
. Предположив, что 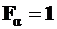 , сделаем переход от напряжений к силам, а затем запишем уравнения равновесия оставшейся части куба с учетом, что
, сделаем переход от напряжений к силам, а затем запишем уравнения равновесия оставшейся части куба с учетом, что  .
.
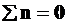 ;
;
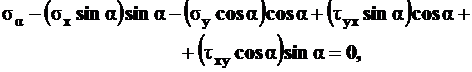
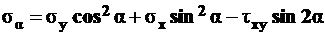 , (4.6)
, (4.6)
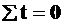 ;
;
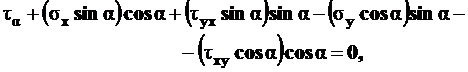
 . (4.7)
. (4.7)
Проанализируем выражение (4.6):
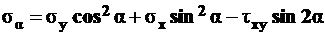 ,
,
для чего продифференцируем его
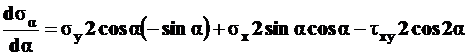 . (4.8)
. (4.8)
Значение первой производной так же, как и в случае линейного напряженного состояния, отличается от выражения для  (4.7) только множителем – 1/2. Следовательно, на площадке, где
(4.7) только множителем – 1/2. Следовательно, на площадке, где 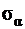 достигнет экстремального значения,
достигнет экстремального значения, 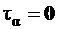 , а сама площадка будет главной. Ее положение может быть определено, если выражение первой производной или выражение (4.7) будут приравнены нулю.
, а сама площадка будет главной. Ее положение может быть определено, если выражение первой производной или выражение (4.7) будут приравнены нулю.
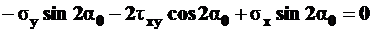 ,
,
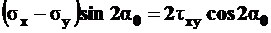 ,
,
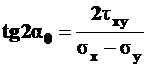 . (4.9)
. (4.9)
Выражение для 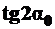 может иметь и другие написания, зависящие от места
может иметь и другие написания, зависящие от места 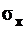 и
и 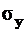 в формуле или при замене
в формуле или при замене  на
на 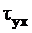 .
.
Если исходные площадки будут главными, то формулы (4.6) и (4.7) примут вид
 , (4.10)
, (4.10)
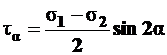 . (4.11)
. (4.11)
Здесь 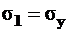 ,
, 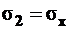 , а
, а 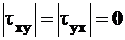 .
.
Из формулы (4.11) следует, что экстремальные значения касательных напряжений будут на взаимно перпендикулярных площадках, образующих углы ± 45° с главными площадками. На них
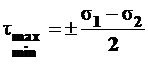 . (4.12)
. (4.12)
Экстремальные значения 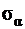 , то есть главные напряжения, могут быть найдены с помощью круга Мора.
, то есть главные напряжения, могут быть найдены с помощью круга Мора.
ЛЕКЦИЯ 5
Обоснование круга Мора
Пусть известные два главных напряжения 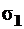 и
и 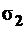 , причем
, причем 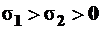 , тогда по формуле (4.10)
, тогда по формуле (4.10)
 .
.
1. Заменим 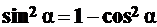 и получим
и получим
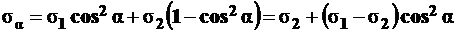 .
.
Отложим 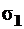 и
и 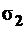 от произвольной точки отсчета «0», как от начала координат (рис. 5.1):
от произвольной точки отсчета «0», как от начала координат (рис. 5.1): 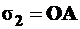 ,
, 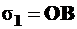 .
.
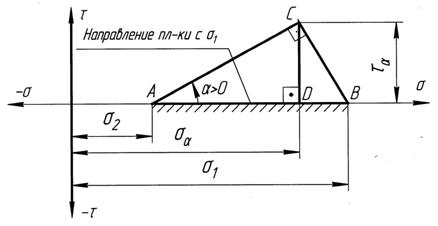
Рис. 5.1 К обоснованию круга Мора
2. Проведем из точки 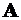 прямую под углом
прямую под углом 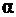 к оси
к оси  , и опустим на нее из точки
, и опустим на нее из точки  перпендикуляр
перпендикуляр 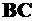 , а из точки
, а из точки  – перпендикуляр
– перпендикуляр 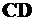 на ось
на ось  , тогда
, тогда
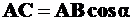 ;
; 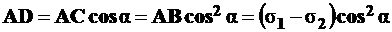 ,
,
поэтому
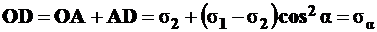 ,
,
то есть расстояние от начала координат 0 до основания перпендикуляра 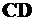 равно нормальному напряжению
равно нормальному напряжению 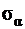 , возникающему на наклонной площадке.
, возникающему на наклонной площадке.
3. 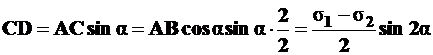 ,
,
то есть высота перпендикуляра 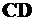 равна касательному напряжению
равна касательному напряжению  , возникающему на наклонной площадке.
, возникающему на наклонной площадке.
Если проводить прямые 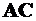 под различными углами
под различными углами 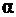 , то точка
, то точка  , оставаясь вершиной прямого угла, будет перемещаться по дуге окружности с диаметром
, оставаясь вершиной прямого угла, будет перемещаться по дуге окружности с диаметром  . Построенная на этом диаметре окружность получила название круга Мора.
. Построенная на этом диаметре окружность получила название круга Мора.
Прямая задача круга Мора
Известны 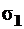 и
и 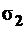 , причем
, причем 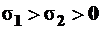 . Необходимо найти
. Необходимо найти 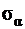 и
и  на площадке, наклоненной к площадке с
на площадке, наклоненной к площадке с 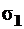 под углом
под углом 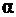 , и
, и 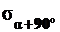 и
и 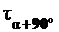 на площадке, сопряженной с ней. Ход решения (рис. 5.2) таков:
на площадке, сопряженной с ней. Ход решения (рис. 5.2) таков:
1. Откладываем от начала координат «0» 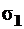 и
и 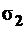 , причем ось
, причем ось  совпадает с направлением площадки, на которой действует
совпадает с направлением площадки, на которой действует 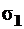 .
.
2. Строим круг на диаметре  , равном
, равном 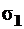 –
– 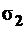 , с центром в точке
, с центром в точке 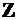 .
.
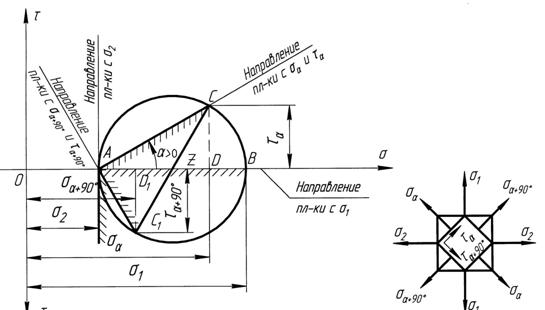
Рис. 5.2 Прямая задача круга Мора
3. Проводим хорду 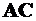 под заданным углом
под заданным углом 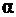 , который всегда отсчитывается от площадки, где заданы напряжения
, который всегда отсчитывается от площадки, где заданы напряжения 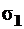 , к площадке, где ищутся напряжения. Таким образом, направление хорды
, к площадке, где ищутся напряжения. Таким образом, направление хорды 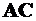 совпадает с направлением площадки, на которой действуют
совпадает с направлением площадки, на которой действуют 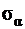 и
и  .
.
4. Опускаем перпендикуляр 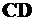 и получаем
и получаем 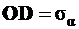 и
и 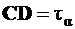 .
.
5. Проводим диаметр 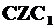 и опускаем перпендикуляр
и опускаем перпендикуляр  на ось
на ось  . Отрезок
. Отрезок 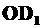 равен
равен 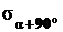 , а перпендикуляр
, а перпендикуляр  равен
равен 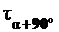 . Направление хорды
. Направление хорды 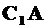 совпадает с направлением площадки, где действуют эти напряжения.
совпадает с направлением площадки, где действуют эти напряжения.
Из прямой задачи круга Мора видно:
1. При  точка
точка  и точка
и точка  совпадут с точкой
совпадут с точкой  , площадка будет главной, так как
, площадка будет главной, так как  , а
, а 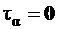 .
.
2. 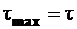 ,
, 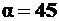 и
и 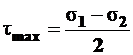 .
.
3. 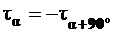 .
.
4. При 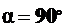 точка
точка  и точка
и точка  совпадут с точкой
совпадут с точкой 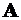 . Это дает направление второй главной площадки, так как
. Это дает направление второй главной площадки, так как  .
.
Вывод из прямой задачи круга Мора: 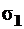 и
и 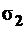 могут быть найдены, если известны
могут быть найдены, если известны 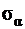 ,
, 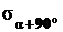 ,
,  и
и 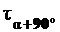 , то есть напряжения на любых взаимно перпендикулярных площадках. Этой цели служит обратная задача круга Мора.
, то есть напряжения на любых взаимно перпендикулярных площадках. Этой цели служит обратная задача круга Мора.
Обратная задача круга Мора
Известны 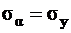 ,
, 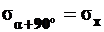 ,
, 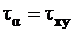 ,
, 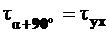 ,
, 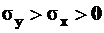 ,
,  (рис. 5.3). Необходимо найти величины главных напряжений и положение главных площадок.
(рис. 5.3). Необходимо найти величины главных напряжений и положение главных площадок.
Ход решения.
1. Откладываем 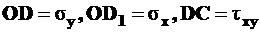 и
и 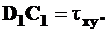
2. Соединяем прямой точки C и C1 и проводим круг на диаметре CC1 с центром в точке Z –получаем 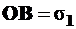 и
и 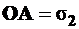 .
.
3. Проводим хорду AC. Угол между AC и AB и есть угол 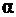 , на который следует делать поворот, чтобы попасть с заданной площадки с
, на который следует делать поворот, чтобы попасть с заданной площадки с 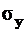 и
и  на площадку с
на площадку с 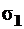 (см. рис. 5.3). Вторая главная площадка перпендикулярна к первой (с
(см. рис. 5.3). Вторая главная площадка перпендикулярна к первой (с 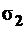 ).
). 
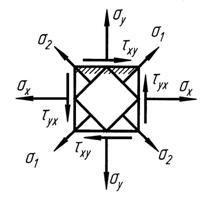
Рис. 5.3 Обратная задача круга Мора
Найдем аналитические выражения для 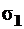 и
и 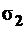 .
.
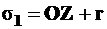 ,
,  , (5.1)
, (5.1)
где r- радиус круга Мора.
Из рис. 5.3 видно, что
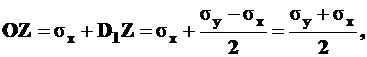 а
а
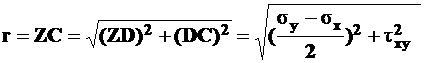 или
или
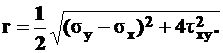
Отсюда по формуле (5.1)
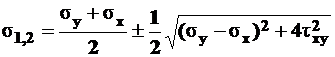 , (5.2)
, (5.2)
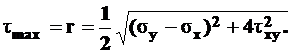 (5.3)
(5.3)
Дата добавления: 2018-02-15; просмотров: 614; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
