Тема 10. Оценка аннуитета с периодом больше года
На практике широко распространены аннуитеты, периоды которых не превосходят базовые периоды начисления процентов. В частности, если базовый период равен году, то период аннуитета не превышает одного года. Однако встречаются ситуации, связанные с аннуитетом, когда его период больше года.
Формулы для оценки будущей и приведенной стоимости аннуитета, период которого больше базового периода начисления процентов, аналогичны формулам для оценки будущей и приведенной стоимости обычного аннуитета. Формулы для оценок аннуитета пренумерандо получаются из соответствующих формул для оценок аннуитета постнумерандо с использованием, как правило, того факта, что денежные поступления пренумерандо начинаются на период (аннуитета) раньше, чем постнумерандо.
Основные формулы раздела
 (10.1)
(10.1)
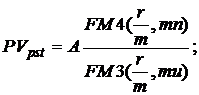 (10.2)
(10.2)
 (10.3)
(10.3)
 (10.4)
(10.4)
 (10.5)
(10.5)
 (10.6)
(10.6)
где А - величина каждого денежного поступления;
 – будущая стоимость аннуитета постнумерандо и пренумерандо;
– будущая стоимость аннуитета постнумерандо и пренумерандо;
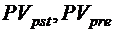 – приведенная стоимость аннуитетов постнумерандо и пренумерандо;
– приведенная стоимость аннуитетов постнумерандо и пренумерандо;
r – ставка за базовый период начисления процентов;
m – количество начислений сложных процентов в периоде;
|
|
|
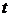 - количество периодов, через которое осуществляются денежные поступления;
- количество периодов, через которое осуществляются денежные поступления;
n – количество периодов;
s – непрерывные проценты;
и - количество периодов, через которое осуществляется денежное поступление.
Типовые задачи с решениями
Задача 1
Работник заключает с фирмой пенсионный контракт на 12 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет поступать по 3 тыс. руб. Требуется определить наращенную сумму к концу действия контракта, если на поступающие суммы будут начисляться:
а) ежегодно сложные проценты по номинальной годовой процентной ставке 24%;
б) ежеквартально сложные проценты по номинальной годовой процентной ставке 24%;
в) непрерывные проценты с силой роста 24% за год.
Решение
Денежные поступления образуют постоянный аннуитет постнумерандо с А = 3 тыс. руб., сроком п = 12 лет и периодом и =2 года. Следовательно, период аннуитета больше базового периода начисления процентов, равного году.
а) В этом случае r = 24%, m = 1, тогда по формуле (10.1):
 тыс. руб.
тыс. руб.
б) Поскольку в этом случае начисление процентов ежеквартальное, то т = 4, тогда по формуле (10.1):
 тыс. руб.
тыс. руб.
в) Полагая s = 0,24, находим по формуле (10.3):
|
|
|
 тыс. руб.
тыс. руб.
Задача 2
Определите сумму, которую необходимо поместить на счет в банке, чтобы в течение 15 лет в конце каждого трехлетнего периода иметь возможность снимать со счета 8 тыс. руб., причем к концу срока полностью выбрать все деньги со счета, если на находящиеся на счете денежные суммы будут начисляться: а) ежегодно сложные проценты по ставке 20%; б) каждые полгода сложные проценты по ставке 20%; в) непрерывные проценты с силой роста 20%.
Решение
Во всех случаях надо определить приведенную стоимость постоянного аннуитета с А=8 тыс. руб., периодом и = 3 года и сроком п = 15 лет.
а) Так как r =20%, то при m = 1, применяя формулу (10.2), получим:
 тыс. руб.
тыс. руб.
б) В этом случае m = 2, r = 20% и поэтому из формулы (10.2) получим:
 тыс. руб.
тыс. руб.
в) Поскольку в этом случае начисляются непрерывные проценты с силой роста s = 0,2, то по формуле (10.4) получим:
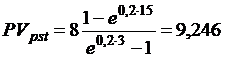 тыс. руб.
тыс. руб.
Задача 3
На счет в банке в начале каждого двухлетнего периода будет поступать по 8 тыс. руб. в течение 10 лет. Требуется определить: а) будущую стоимость аннуитета; б) приведенную стоимость аннуитета, если на поступающие суммы будут ежегодно начисляться декурсивные сложные проценты по ставке 22% годовых.
Решение
Согласно условию имеем аннуитет пренумерандо с членом А =14 тыс. руб., периодом u =2 года и сроком n=10 лет. Сложная процентная ставка r =22% годовых и число начислений процентов m = 1.
|
|
|
а) В соответствии с формулами (10.1) и (10.5) получим:
 тыс. руб.
тыс. руб.
б) По формуле (10.2) и (10.6) получим:
 тыс. руб.
тыс. руб.
Дата добавления: 2018-02-15; просмотров: 1328; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
