Тема 6. Инфляция и начисление сложных и непрерывных процентов

⇐ ПредыдущаяСтр 5 из 12Следующая ⇒

Для оценки наращенной суммы с учетом ее обесценения полученную величину делят на индекс инфляции за время осуществления наращения. Если множитель наращения равен индексу инфляции, то соответствующее наращение лишь нейтрализует действие инфляции.

При инфляции выделяют следующие виды процентных ставок: номинальную, реальную, положительную. Иногда ставку с поправкой на инфляцию называют брутто-ставкой.

Для обеспечения реального роста стоимости первоначального капитала при инфляции необходимо исходную ставку увеличивать (индексировать). Выбор величины такой индексированной ставки определяется поставленными целями. Для обеспечения реальной доходности согласно исходному коэффициенту наращения необходимо так индексировать исходную ставку (увеличить на инфляционную премию), чтобы новый коэффициент наращения полностью компенсировал потери из-за инфляции.

Формула Фишера определяет значение сложной годовой процентной ставки, обеспечивающей при известном годовом темпе инфляции реальную эффективность кредитной операции. Эта формула по существу показывает ту величину, называемую инфляционной премией, которую необходимо прибавить к исходной ставке доходности для компенсации инфляционных потерь. При малом темпе инфляции и невысокой процентной ставке (эта ситуация типична для стран с развитой рыночной экономикой) пользуются и приближенным вариантом формулы Фишера.

Типовые задачи с решениями

Задача 1

На вклад начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно. Какова должна быть годовая номинальная процентная ставка, при которой происходит реальное наращение капитала, если ежемесячный темп инфляции составляет 3%?

Решение

а) Обозначим через 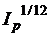среднемесячный (т.е. за полгода) индекс инфляции, тогда 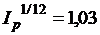и при к=12 находим индекс инфляции за год:

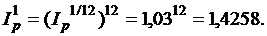
Пусть r – процентная ставка при ежегодном начислении сложных процентов, тогда значение ставки, лишь нейтрализующей действие инфляции, находится из равенства 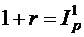(т.е. множитель наращения за год приравнивается к годовому индексу инфляции). Таким образом:

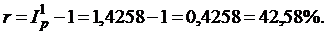
Следовательно, реальное наращение капитала будет происходить только при процентной ставке, превышающей 42,58% годовых.

б) При ежеквартальном начислении сложных процентов для определения номинальной ставки, лишь нейтрализующей действие инфляции, пользуемся равенством:

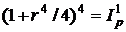, откуда:

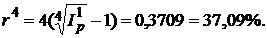
Таким образом, положительная процентная ставка при ежеквартальном начислении сложных процентов превышает 37,09% годовых.

в) В случае ежемесячного начисления процентов пользуемся равенством:

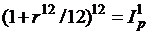, откуда:

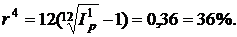
Итак, в данной ситуации реальное наращение исходит при номинальной процентной ставке, большей, чем 36% годовых. В этом случае ответ можно было дать сразу, поскольку для осуществления реального наращения капитала его относительный рост за месяц должен превышать темп инфляции за это же время. Следовательно, 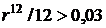, поэтому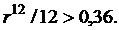

Задача 2

Номинальная процентная ставка, компенсирующая при наращении действие инфляции, 52% годовых. Определите полугодовую инфляцию, если начисление сложных процентов осуществляется каждый квартал:

Решение

Приравняем годовой индекс инфляции к множителю наращения за год. Полагая 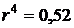, получим:

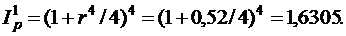
Поэтому индекс инфляции за полгода (0,5 года) составит:

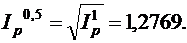
Следовательно, темп инфляции за полгода в среднем равен 27,69%.

Задача 3

На некоторую сумму в течение трех лет будут начисляться непрерывные проценты. По прогнозам инфляция за это время за каждый год последовательно составит 15, 20 и 10 процентов. Какова должна быть сила роста за год, чтобы сумма покупательной способности не уменьшилась?

Решение

Поскольку индекс инфляции за первый год равен 1,15, за второй – 1,2 и за третий – 1,1, то индекс инфляции за 3 года составит:

1,15×1,2×1,1=1,518.

Пусть s – сила роста за год, позволяющая первоначальной сумме только сохранить свою покупательную способность. Приравнивая индекс инфляции за три года к множителю наращения за это же время, получим: 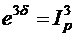, отсюда:

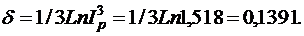
Следовательно, сила роста (интенсивность наращения) должна превышать 13,91% за год.

Задача 4

На вклад в течение 15 месяцев начисляются проценты: а) по схеме сложных процентов; б) по смешанной схеме. Какова должна быть процентная ставка, при которой происходит реальное наращение капитала, если каждый квартал цены увеличиваются на 8%?

Решение

а) Так как темп инфляции за каждый квартал равен 8%, то индекс инфляции за каждый квартал (0,25 года) равен 1,08. Поэтому индекс инфляции за 15 месяцев (1,25 года, или 5 кварталов) составит:

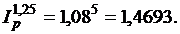
Обозначим через r искомую годовую процентную ставку и приравняем этот индекс инфляции к множителю наращения при использовании схемы сложных процентов:

(1+г)^1,25 =1,4693.

Отсюда:

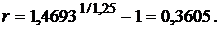
Таким образом, в этом случае ставка должна превышать 36,05% годовых.

При рассмотрении этого случая можно было рассуждать и таким образом. При инфляции 8% за каждый квартал годовой темп инфляции составит 1,08⁴–1=0,3605=36,05%. Реальное же наращение капитала будет происходить, если годовая процентная ставка превышает годовой темп инфляции, т.е. г > 36,05%.

б) Пусть теперь применяется смешанная схема. Приравнивая индекс инфляции за 1,25 года к множителю наращения, получим квадратное уравнение относительно r:

(1+r)×(1+0,25r)= 1,4693

Решая уравнение, определяем корни: r= –5,3508, r =0,3508.

Очевидно, что по смыслу первый корень не подходит. Следовательно, при использовании смешанной схемы ставка должна превышать 35,08% годовых. «Граничное» значение ставки в этом случае получили почти на 1% меньше, чем в предыдущем, что объясняется большей эффективностью смешанной схемы начисления по сравнению со схемой сложных процентов.

Обратим внимание, что для ответа на вопрос в данном случае необходимо фактически решить неравенство:

(1+r)(1+0,25r)>1,4693.

Задача 5

На вклад 28 тыс. руб. ежеквартально начисляются сложные проценты по номинальной годовой процентной ставке 40%. Оцените сумму вклада через 21 месяц с точки зрения покупательной способности, если ожидаемый темп инфляции – 2% в месяц. Какова должна быть величина номинальной положительной процентной ставки? Как изменится ситуация, если темп инфляции будет 3,5% в месяц?

Решение

При наращении сложными процентами при начислении процентов несколько раз за год сумма вклада составит:

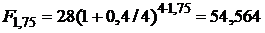тыс.руб.

Индекс инфляции за 1,75 года при темпе инфляции 2% в месяц составит:

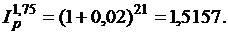
Величина вклада с точки зрения ее покупательной способности:

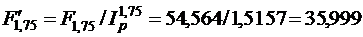тыс. руб.

Вычитая из этой величины первоначальную сумму, найдем реальный доход владельца вклада:

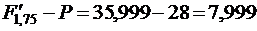тыс. руб.

При темпе инфляции 3,5% в месяц: 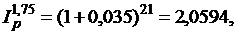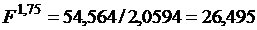тыс. руб. и реальный доход вкладчика составит 26,495 –28 = – 1,505 тыс. руб., т.е. в этом случае вкладчик с точки зрения покупательной способности потерпит убытки. В данных, условиях для положительной процентной ставки должно выполняться неравенство:

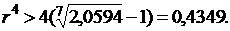
Следовательно, номинальная процентная ставка (40%) меньше положительной процентной ставки.

Дата добавления: 2018-02-15; просмотров: 1526; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!