Тема 3. Сложная процентная ставка

 

Схема сложных процентов предполагает их капитализацию, т.е. база, с которой происходит начисление, посто­янно возрастает на величину начисленных ранее процентов. Оче­видно, что более частое начисление сложных процентов обеспечи­вает более быстрый рост наращиваемой суммы.

Для кредитора более выгодна схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода); более выгодна схема сложных процентов, если срок суды превышает один год (проценты начисляются ежегодно); обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

При начислении процентов за дробное число лет может использоваться схема сложных процентов, либо смешанная схема, предусматривающая начисление сложных процен­тов за целое число лет и простых процентов за дробнуючасть года.

Математическим дисконтированием (дисконтированием по сложной процентной ставке) называется задача нахождения такой величины первоначального капитала, которая через заданное количество времени при наращении по сложной процентной ставке обеспечит получение планируемой суммы.

Основные формулы раздела

 

F=P (1 + r)ⁿ;                                       (3.1)

P = F / (1 + r)ⁿ;                                             (3.2)

r=(F/P)^1/n–1;                                (3.3)

 

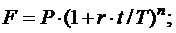                        (3.4)

F = P (1 + r/m)^nm;                         (3.5)

 

F=P(1+r/m)^w+f;                        (3.6)

F=P(1+r/m)^w×(1+f×r/m),                 (3.7)

 

где F – наращенная сумма;

P – вложенная сумма;

n – количество лет;

r – сложнаяпроцентная ставка;

t – продолжительность финансовой операции в днях;

T – количество дней в году;

m – количество начислений процентов в году;

w – целая часть периода финансовой операции;

f – дробная часть периода финансовой операции.

Типовые задачи с решениями

 

Задача 1

На вашем счёте в банке 120 тыс. руб. Банк платит 12,5 % годовых. Вам предлагают войти всем капиталом в организацию совместного предприятия, обещая удвоение капитала через 5 лет. Принимать ли это предложение?

Решение

Для решения задачи используем формулу (3.1.):

Если мы вложим деньги в банк, то через 5 лет получим следующую сумму:

F = 120 тыс.руб.(1 + 0,125)⁵ = 366 тыс.руб.

Если мы войдем всем капиталом в организацию совместного предприятия, то наш капитал удвоится:

F = 120 тыс.руб. × 2 = 240 тыс.руб.

Следует вложить деньги в банк, так как в этом случае мы получим большее приращение капитала.

 

Задача 2

Вы имеете 20 тыс. руб. и хотели бы удвоить эту сумму через 5 лет. Каково минимально приемлемое значение процентной ставки?

 

Решение

Для решения данной задачи используем формулу (3.2):

              r=(2×20 тыс.руб/ 20 тыс.руб)^1/5–1=14,9%.

Таким образом, минимальное приемлемое значение процентной ставки составляет 14,9%.

                       

Задача 3

Рассчитайте наращенную сумму с исходной суммы в 20 тыс. руб. при размещении её в банке на условиях начисления: а) простых и б) сложных процентов, если годовая ставка 15%, а периоды наращения 90 дней, 180 дней, 1 год, 5 лет, 10 лет.

Решение

Для решения задачи используем формулы (1.3) и (3.4).

При простых процентах:

- период наращения 90 дней: F= 20 тыс. руб. (1 + 0,15×90/360) = =20750 руб.

- период наращения 180 дней: F= 20 тыс. руб. (1 + 0,15×180/360)= =21500 руб.

- период наращения 1 год: F = 20 тыс. руб. (1 +0,15 × 1) = 23 тыс.руб.

- период наращения 5 лет: F = 20 тыс. руб. (1 +0,15 × 5) = 35 тыс.руб.

- период наращения 10 лет: F = 20 тыс. руб. (1 + 0,15× 10) = 50 тыс.руб.

При сложных процентах:

- период наращения 90 дней: F = 20 тыс. руб. (1 + 0,15)^90/360 = 20711 руб.

- период наращения 180 дней: F = 20 тыс. руб. (1+ 0,15)^180/360 = 21448 руб.

- период наращения 1 год: F = 20 тыс. руб. (1 + 0,15)¹ = 23 тыс.руб.

- период наращения 5 лет: F = 20 тыс. руб. (1 + 0,15)⁵ = 40227 руб.

- период наращения 10 лет: F = 20 тыс. руб. (1 + 0,15)¹⁰ = 80911 руб.

 

Задача 4

Через 4 года ваш сын будет поступать в университет на коммерческой основе. Плата за весь срок обучения составит 5600 долл., если внести её в момент поступления в университет. Вы располагаете в данный момент суммой в 4000 долл. Под какую минимальную процентную ставку нужно положить деньги в банк, чтобы накопить требуемую сумму?

Решение

Для решения задачи используем формулу (3.3):

           r=(5600$/4000$)^1/4–1=8,78%.

Таким образом, для того чтобы накопить нужную сумму, минимальная ссудная процентная ставка должна составлять 8,78%.

 

Задача 5

За выполненную работу предприниматель должен получить 60 тыс. руб. Заказчик не имеет возможности рассчитаться в данный момент и предлагает отложить срок уплаты на 2 года, по истечении которых он обязуется выплатить 70 тыс. руб. Выгодно ли это предпринимателю, если приемлемая норма прибыли составляет 10%? Какова минимальная ставка, которая делает подобные условия невыгодными для предпринимателя?

 

Решение

Для решения задачи используем формулу (3.1).

Будущая стоимость 60 тыс.руб. через 2 года при норме прибыли 10% составит:

F = 60 тыс.руб. (1 + 0,1)² = 72,6 тыс.руб.

Это больше, чем 70 тыс. руб., поэтому нам не выгодно ждать расплаты 2 года.

Для расчета минимальной ставки, которая делает условия невыгодными, воспользуемся формулой (3.3):

r = (70 тыс. руб. / 60 тыс. руб.)^1/2 – 1 = 8%.

Задача 6

Рассчитайте будущую стоимость 1000 долл. для следующих ситуаций:

а) 5 лет, 8% годовых, ежегодное начисление процентов;
     б) 5 лет, 8 % годовых, полугодовое начисление процентов;
     в) 5 лет, 8 % годовых, ежеквартальное начисление процентов.

 

Решение

Для решения задачи воспользуемся формулой (3.5).

При ежегодном начислении процентов F=1000$ (1 + 0.08/1)⁵ = 1469$.

При полугодовом начислении процентов F=1000$(1+0.08/2)^2*5= 1480$.

При ежеквартальном начислении процентов F=1000$(1+0.08/4)^4*5= 1486$.

Задача 7

Банк предоставил ссуду в размере 5000 долл. на 39 месяцев под 20% годовых на условиях полугодового начисления процентов. Рассчитайте возвращаемую сумму при различных схемах процентов: а) схема сложных процентов; б) смешанная схема.

 

Решение

Для решения воспользуемся формулами:

1) Схема сложных процентов – формула (3.6) при w=6;

     f=3,25×2–6=0,5; m=2:

F=5000$(1+0,2/2)^6+0,5=9290,1$;

2) Смешанная схема – формула (3.7) при w=6; f=0,5; m=2:

F=5000$(1+0,2/2)^6.(1+0,5×0,2/2)=9300,69$.

 

Задача 8

Банк предлагает 15% годовых. Чему должен быть равен первоначальный вклад, чтобы через 3 года иметь на счёте 50 тыс. руб.?

 

 

Решение

Для решения задачи используем формулу (3.2):

P = 50 тыс.руб./ (1 + 0,15)³ = 32876 руб.

Задача 9

Через 5 лет ваш сын будет поступать в университет на коммерческой основе. В том случае, если оплата университетской программы будет осуществляться в момент поступления авансом за весь срок обучения, можно получить существенную скидку, а сумма требуемого платежа составит 7500 долл. Вы планируете также через 3 года сменить свой автомобиль, потратив на него 15 тыс. долл. Каким должен быть взнос в банк, чтобы накопить требуемые суммы, если банк предлагает ставку в размере 12%?

 

Решение

Для решения задачи воспользуемся формулой (3.2).

Решение этой задачи происходит в два этапа:

1) P₁ =7500$/(1+0,12)⁵=4255,7$.

2) P₂=15000$/(1+0,12)³=10676,7$.

Таким образом, сумма минимального взноса в банк составит:

P=P₁+P₂=4255,7$+10676,7$=14932,4$   

F = 100 тыс.руб× (1 + 0,08/2)^5*2=148,024 тыс.руб.

 

Задача 10

Фирме нужно накопить 2 млн.долл., чтобы через 10 лет приобрести здание под офис. Наиболее безопасным способом накопления является приобретение безрисковых государственных ценных бумаг, генерирующих годовой доход по ставке 8 % при полугодовом начислении процентов. Каким должен быть первоначальный вклад фирмы?

Решение

Для определения первоначального взноса определим Р из формулы (3.5):

P = F / (1 + r/m)^nm;

P = 2000000 / (1 + 0,08/2)^10*2=912773,89$.

 

---

Дата добавления: 2018-02-15; просмотров: 7655; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!