Тема 2. Простые учетные ставки
СОДЕРЖАНИЕ
Тема 1. Простые процентные ставки.. 4
Основные формулы раздела. 5
Типовые задачи с решениями. 5
Тема 2. Простые учетные ставки.. 7
Основные формулы раздела. 7
Типовые задачи с решениями. 8
Тема 3. Сложная процентная ставка.. 10
Основные формулы раздела. 10
Типовые задачи с решениями. 11
Тема 4. Сложная учетная ставка.. 15
Основные формулы раздела. 15
Типовые задачи с решениями. 16
Тема 5. Эквивалентные и эффективные ставки.. 20
Основные формулы раздела. 20
Типовые задачи с решениями. 21
Тема 6. Инфляция и начисление сложных и непрерывных процентов.. 26
Типовые задачи с решениями. 26
Тема 7. Прямая и обратная задача оценки денежного потока 31
Основные формулы раздела. 32
Типовые задачи с решениями. 32
Тема 8. Прямая и обратная задача оценки аннуитета.. 36
Основные формулы раздела. 36
Типовые задачи с решениями. 37
Тема 9. Непрерывный и переменный аннуитеты.. 42
Основные формулы раздела. 42
Типовые задачи с решениями. 43
Тема 10. Оценка аннуитета с периодом больше года.. 47
Основные формулы раздела. 47
Типовые задачи с решениями. 48
Тема 11. Управление оборотным капиталом предприятия 50
Типовые задачи с решениями. 51
Тема 12. Операционный анализ. 56
Типовые задачи с решениями. 64
Тема 13. Расчет средневзвешенной стоимости капитала 75
Типовые задачи с решениями. 75
|
|
|
Контрольная работа.. 79
Тема 1. Простые процентные ставки
Денежные ресурсы, участвующиев финансовой операции, имеют временную ценность, смысл которой может быть выражен следующим утверждением: одна денежная единица, имеющаяся в распоряжении инвестора в данный момент времени, более предпочтительна, чем та же самая денежная единица, но ожидаемая к получению в некотором будущем. Эффективность любой финансовой операции, предполагающей наращение исходной суммы P до ожидаемой в будущем к получению суммы F (F>P), может быть охарактеризована ставкой.
Процентная ставка рассчитывается отношением наращения (F–P) к исходной (базовой) величине P.
Схемапростых процентов предполагает неизменность базы,с которойпроисходит начисление.
В финансовых вычислениях базовым периодом являетсягод,поэтому обычно говорят о годовой ставке. Вместе с тем достаточно широко распространены краткосрочные операции продолжительностью до года. В этом случае за основу берется дневная ставка, причем в зависимости от алгоритмов расчета дневной ставки и продолжительности финансовой операции результаты наращения будут различными. Используются три варианта расчета: а) точный процент и точное число дней финансовой операции – обозначение 365/365; б) обыкновенный процент и точное число дней финансовой операции - обозначение 365/360; в) обыкновенный процент и приблизительное число дней финансовой операции - обозначение 360/360.
|
|
|
Математическое дисконтирование является процессом, обратным к наращению первоначального капитала. При математическом дисконтировании решается задача нахождения такой величины капитала (называемой приведенной стоимостью), которая через заданное время при наращении по данной процентной ставке будет равна сумме, ожидаемой к получению (уплате) через заданное время.
Возможно финансовое соглашение, предусматривающее изменение во времени учетной ставки.
Любая финансовая операция предусматривает участие, как минимум, двух сторон: кредитора (инвестора) и заемщика (получателя финансовых ресурсов); это обстоятельство является существенным для вынесения суждения об эффективности некоторой операции. Так, экономическая интерпретация ставки вообще и ее значения в частности зависит от того, с чьих позиций – кредитора или заемщика - она дается. Для кредитора ставка характеризует его относительный доход; для заемщика – его относительные расходы. Поэтому кредитор всегда заинтересован в высокой ставке или в повышении ставки; интересы заемщика – прямо противоположны.
|
|
|
Основные формулы раздела
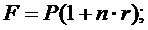 (1.1)
(1.1)
 (1.2)
(1.2)
F=P(1+r×t /T); (1.3)
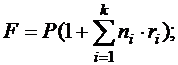 (1.4)
(1.4)
 (1.5)
(1.5)
где F – наращенная сумма;
P – вложенная сумма;
n – количество лет;
r – простая процентная ставка;
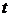 - продолжительность финансовой операции в днях;
- продолжительность финансовой операции в днях;
 - количество дней в году.
- количество дней в году.
Типовые задачи с решениями
Задача 1
Вы поместили в банк вклад 10 тыс. руб. под простую процентную ставку 26% годовых. Какая сумма будет на счете через 3 года? Какова величина начисленных процентов?
Решение
По формуле (1.1.) при Р=10000, n=3, r =26 получаем:
F=10 ×(1+3×0,26)=17,8 тыс. руб.
Величина начисленных процентов составит:
17,8–10=7,8 тыс. руб.
Задача 2
На какой срок необходимо поместить денежную сумму под простую процентную ставку 28% годовых, чтобы она увеличилась в 1,5 раза?
Решение
Искомый срок определяем из равенства множителя наращения величине 1,5:
|
|
|
1+n×0,28=1,5, поэтому:
n=1,5/0,28=1.786 лет= 1 год 287 дней.
Задача 3
Предоставлена ссуда 3000 долл. 16 января с погашением через 9 месяцев под 25 % годовых (год не високосный). Рассчитайте сумму к погашению при различных способах начисления процентов: а) обыкновенный процент с точным числом дней; б) обыкновенный процент с приближенным числом дней; в) точный процент с точным числом дней.
Решение
Для решения этой задачи воспользуемся формулой наращения капитала по простой ставке ссудного процента (1.3):
F=P(1+r×t /T);
а) используя обыкновенный процент с точным числом дней (рассчитанное по финансовым таблицам):
t=289–16=273 дня,
получим следующий результат:
F=3000$(1+0,25×273/360)=3568,75$;
б) используя обыкновенный процент с приближенным числом дней:
t=9×30=270 дней,
получим:
F=3000$(1+0,25×270/360)=3562,5$;
в) используя точный процент с точным числом дней:
t=273 дня,
получим:
F=3000$(1+0,25×273/365)=3560,96$.
Задача 4
В финансовом договоре клиента с банком предусмотрено погашение долга в размере 8,9 тыс. руб. через 120 дней при взятом кредите в размере 8 тыс. руб. Определить доходность такой сделки для банка в виде годовой процентной ставки при использовании банком простых обыкновенных процентов.
Решение
Подставляя в формулу (1.3) значения F=8,9 тыс. руб., P= 8 тыс. руб., t= 120 дней, T=360 дней, получим:
r=360×(8,9–8)/ (8×120)= 0,3375=33,75%.
Задача 5
Господин Х поместил 16 тыс. руб. в банк на следующих условиях: в первые полгода процентная ставка равна 24% годовых, каждый следующий квартал ставка повышается на 3%. Какая сумма будет на счете через полтора года, если проценты начисляются на первоначальную сумму вклада?
Решение
Применяя формулу (1.4), получим:
F=16×(1+0.5×0,24+0,25×0,27×+0,25×0,3+0,25×0,33+0,25×0,36)=
=22,96 тыс. руб.
Тема 2. Простые учетные ставки
Учетная ставка рассчитывается отношением наращения (F–P) к ожидаемой в будущем к получению, или наращенной, величине F.
Банковское (коммерческое) дисконтирование применяется в ситуации предварительного начисления простого процента, например, при операции по учету векселя, заключающейся в покупке банком векселя у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю в конце срока. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя.
Банковское дисконтирование нельзя осуществить во всех ситуациях, например, по достаточно большой учетной ставке и задолго до срока платежа.
Математическое дисконтирование выгоднее для векселедержателя, а банковское – для банка.
При применении наращения по простой учетной ставке величина начисляемых процентов с каждым годом увеличивается, при наращении капитала по простой процентной ставке капитал ежегодно увеличивается на одну и ту же величину. Простая учетная ставка обеспечивает более быстрый рост капитала, чем такая же по величине процентная ставка.
Возможно финансовое соглашение, предусматривающее изменение во времени учетной ставки.
При продолжительности финансовой операции в днях, возможно использование точных и приближенных процентов для учетной ставки.
Основные формулы раздела
 (2.1)
(2.1)
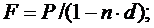 (2.2)
(2.2)
 (2.3)
(2.3)

D=F–P; (2.4)
 (2.5)
(2.5)
 (2.6)
(2.6)
где F – наращенная сумма;
P – вложенная сумма;
n – количество лет;
d – простаяучетная ставка;
t – продолжительность финансовой операции в днях;
 - количество дней в году;
- количество дней в году;
 – дисконт.
– дисконт.
Типовые задачи с решениями
Задача 1
В банк 6 мая предъявлен для учета вексель на сумму 14 тыс. руб. со сроком погашения 10 июля того же года. Банк учитывает вексель по учетной ставке 40% годовых, используя способ 365/360. Определить сумму, получаемую векселедержателем от банка, и комиссионные, удерживаемые банком за свою услугу. За какое время до срока платежа операция учета векселя имеет смысл?
Решение
По формуле (2.3) при F=14 тыс.руб., n=65/360, d=0,4 имеем:
Р=14×(1–0,4 ×65/365)=12,989 тыс. руб.
Комиссионные банка определяются как:
F–P= 14–12,989=1,011 тыс. руб.
Учет векселя по учетной ставке имеет смысл при d<1/n, для данного случая для n< 2,5 года. При n>2,5 года сумма Р, которую должен получить владелец векселя при его учете, становится отрицательной.
Задача 2
Вексель на сумму 9 тыс. руб. учитывается по простой учетной ставке за 120 дней до погашения с дисконтом 600 руб. в пользу банка. Определить величину годовой учетной ставки при временной базе 360 дней в году.
Решение
По формуле (2.5) при F=9 тыс. руб., F–P=0,6 тыс. руб., t=120 дней, T=360 дней, получим:
d= 0,6×360/(9×120)=0,20=20% годовых.
Задача 3
В банк предъявлен вексель на сумму 50 тыс. руб. за полтора года до его погашения. Банк согласен учесть вексель по переменной простой учетной ставке, установленной следующим образом: первые полгода – 30% годовых, следующие полгода – 36% годовых, затем каждый квартал ставка повышается на 2%. Определите дисконт банка и сумму, которую получит векселедержатель.
Решение
По формулам (2.3), (2.4) дисконт за первое полугодие составит:
50× 0,5×0,3 тыс. руб.
Дисконт за второе полугодие составит: 50×0,5×0,36 тыс.руб.
Дисконт за первый квартал третьего полугодия составит:
50×0,25×(0,36+0,2).
Дисконт за второй квартал третьего полугодия составит:
50×0,25×(0,38+0,2).
Суммируя полученные величины, находим дисконт за полтора года:
D=50×(0,5×0,3+0,5×0,36+0,25×0,38+0,25×0,4)=26,25 тыс. руб.
Владелец векселя получит 50–26,25=23,75 тыс. руб.
Задача 4
При учете предъявленного векселя на сумму 30 тыс. руб. за 40 дней до его погашения доход банка составил 1,5 тыс. руб. Определить доходность этой операции для банка в виде простой годовой процентной ставки при расчетном количестве дней в году, равном 360.
Решение
Находим сумму, выплаченную предъявителю векселя: Р=30–1,5=28,5 тыс.руб.
Затем по формуле (1.5) при F–Р=1,5; Р=28,5; t=40; Т=360, находим:
r= 1,5×360/(2,8×40) = 0,4737=47,37%.
Задача 5
Вексель учитывается банком по простой учетной ставке 39% годовых. Определите доходность такой финансовой операции для банка в виде простой годовой процентной ставки.
Решение
Пусть к учету предъявлен вексель на некоторую сумму F.
Определяя доход банка как разность F–Р и применяя формулу (2.3), получим, что доход банка составит:
F×0,39×120/360 = 0,13 F, а предъявитель векселя получит сумму, равную F–0,13× F=0,87× F.
Следовательно, по формуле (1.6) в виде простой годовой процентной ставки составит:
0,13 F×360/(0,87 F×120)=0, 4483=44,83%.
Дата добавления: 2018-02-15; просмотров: 3741; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
