Тема 4. Сложная учетная ставка
Дисконтирование по сложной учетной ставке осуществляется в ситуации предварительного начисления сложного процента, т.е. когда сложный процент (например, за кредит) начисляется в момент заключения финансового соглашения. В этом случае в начале каждого периода начисления проценты начисляются не на одну и ту же величину (как при дисконтировании по простой учетной ставке), а каждый раз на новую, полученную в результате дисконтирования, осуществленного в предыдущем периоде.
Для лица, осуществляющего антисипативное начисление процентов более выгодна сложная учетная ставка, если срок учета менее одного года; более выгодна простая учетная ставка, если срок учета превышает один год.
Если продолжительность финансовой операции не равна целому числу лет, то при определении стоимости учетного капитала используют либо сложную учетную ставку, либо смешанную схему (сложная учетная ставка для целого числа лет и простая учетная ставка для дробной части года). Стоимость учетного капитала больше при использовании смешанной схемы.
Основные формулы раздела
 (4.1)
(4.1)
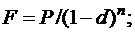 (4.2)
(4.2)
 (4.3)
(4.3)
 (4.4)
(4.4)
 (4.5)
(4.5)
 (4.6)
(4.6)
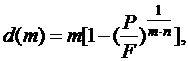 (4.7)
(4.7)
где F – наращенная сумма;
P – вложенная сумма;
n – количество лет;
d – сложная учетная ставка;
m – количество начислений процентов в году;
w – целая часть периода финансовой операции;
f – дробная часть периода финансовой операции.
Типовые задачи с решениями
Задача 1
Найдите величину дисконта, если долговое обязательство на выплату 40 тыс. руб. учтено за 3 года до срока погашения по сложной учетной ставке: а) 20% годовых; б) 25% годовых.
Решение
а) По формуле (4.1) при n=3, F=40 тыс. руб., d=0,2 получим:

Поэтому дисконт составит 40–28,28=19,52 тыс. руб.
б) По формуле (4.1) при n=3, F=40 тыс. руб., d=0,25 получим:
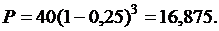
Поэтому дисконт составит 40–16,875=23,125 тыс. руб.
Задача 2
Вексель на сумму 70 тыс. руб. со сроком погашения через 4 года учтен за 32 месяца по сложной учетной ставке 24% годовых. Определить суммы, которые получит предъявитель векселя при различных способах учета.
Решение
При применении сложной учетной ставки воспользуемся формулой (4.1) при n=32/12=8/3, F=70 тыс. руб., d=0,24, поэтому:

Владелец векселя получит 33, 672 руб.
При применении смешанной схемы воспользуемся формулой (4.4) при w=2, f=2/3:

Таким образом, владелец векселя получит большую сумму при использовании смешанной схемы.
Задача 3
Рассчитать дисконтированную сумму при учете 1 млн. руб. по простой и сложной учетной ставкам, если годовая учетная ставка равна 18% годовых и учет происходит за 30 дней, 90 дней, 180 дней, 1 год, 2 года, 3 года, 5 лет. Каждый год считать равным 360 дней.
Решение
Применяя формулу (2.1) для простой учетной ставки и формулу (4.1) для сложной учетной ставки при F=1 млн. руб., d=0,18 и различных n, получим:
Млн. руб.
| Способ дисконтирования | 30 дней n=1/12 | 90 дней n=1/4 | 180 дней n=1/2 | 1 год n=1 | 2 года n=2 | 3 года n=3 | 5 лет n=5 |
| Простая ставка | 0.985 | 0.955 | 0.91 | 0.82 | 0.64 | 0.46 | 0.1 |
| Сложная ставка | 0.984 | 0.952 | 0.905 | 0.82 | 0.67 | 0.55 | 0.37 |
Задача 4. Долговое обязательство на выплату 46 тыс. руб. учтено за 4 года до срока погашения. Определите полученную сумму. Если производилось: а) полугодовое; б) поквартальное; в) ежемесячное дисконтирование по сложной учетной ставке 24% годовых.
Решение
а) При F=46; d=0,24; n=4; m=2 по формуле (4.3) получим:

б) При F=46; d=0,24; n=4; m=4 по формуле (4.3) получим:
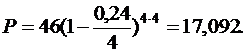
в) При F=46; d=0,24; n=4; m=12 по формуле (4.3) получим:
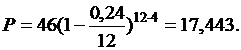
Сравнивая полученные результаты, делаем вывод, что с ростом числа осуществлений операций дисконтирования в году величина учетного капитала возрастает.
Задача 5
Вклад в размере 20 тыс. руб. помещен в банк на 5 лет, причем предусмотрен следующий порядок начисления сложных процентов по плавающей годовой учетной ставке: в первые 2 года – 16%, в следующие 2 года – 19%, в оставшийся год – 23%. Определить наращенную сумму. При использовании какой постоянной учетной ставки можно получить такую же сумму?
Решение
Наращенную сумму за первые 2 года определяем по формуле (4.2) при Р=20; n=2; d=0,16:

Наращенную сумму за следующие 2 года определяем по формуле (4.2) при Р=20; n=2; d=0,19:

Наращенную сумму за последний год определяем по формуле (4.2) при Р=20; n=2; d=0,23:
 тыс. руб.
тыс. руб.
Постоянную годовую учетную ставку d, дающую тот же результат, находим из равенства:

d=0,1864=18,64%.
Задача 6
За долговое обязательство в 80 тыс. руб. банком было выплачено 62 тыс. руб. За какое время до срока погашения было учтено это обязательство, если банком использовалась: а) годовая сложная учетная ставка 28% годовых; б) годовая простая учетная ставка 28% годовых?
Решение
а) По формуле (4.6) при Р=62 тыс. руб., F=80 тыс. руб.; m=1; d=0,28; получим:
 года= 280 дней.
года= 280 дней.
б) По формуле (2.6) при Р=62 тыс. руб., F=80 тыс. руб.; d=0,28; получим:
 года= 290 дней.
года= 290 дней.
Задача 7
Вексель был учтен за 2, 5 года до срока его погашения, при этом владелец векселя получил четверть от написанной на векселе суммы. По какой годовой учетной ставке был учтен этот вексель, если производилось: а) поквартальное дисконтирование; б) ежемесячное дисконтирование.
Решение
а) по формуле (4.7) при P=0,25F; n=2,5; m=4, получим:
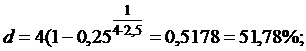
б) по формуле (4.7) при P=0,25F; n=2,5; m=12, получим:

Задача 8
Согласно финансовому соглашению банк начисляет по полугодиям проценты на вклады по сложной учетной ставке 28% годовых. Определить в виде простой годовой процентной ставки стоимость привлеченных средств для банка при их размещении на 3 месяца.
Решение
Стоимость привлеченных средств найдем по формуле (1.5), где Р –использованная сумма средств; (F–P) – проценты, выплаченные за использование суммы Р в течение времени n; F определяется из формулы (4.5) при n=0,25; m=2; d=0,28:

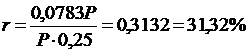 годовых.
годовых.
Дата добавления: 2018-02-15; просмотров: 3727; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
