Тема 8. Прямая и обратная задача оценки аннуитета
Аннуитет представляет собой частный случай денежного потока. Известны два подхода к его определению. Согласно первому подходу, аннуитет – однонаправленный денежный поток, элементы которого имеют место через равные временные интервалы. Второй подход накладывает дополнительное ограничение, а именно, элементы денежного потока одинаковы по величине.
Ускоренные методы оценки денежных потоков основаны на применении мультиплицирующих и дисконтирующих множителей, которые табулированы в специальных финансовых таблицах. Таблицы инвариантны по отношению к виду потока – постнумерандо или пренумерандо; оценки для потока пренумерандо отличаются от соответствующих оценок для потока постнумерандо на величину множителя (1+г), где г – ставка в долях единицы.
В финансовой математике разработаны универсальные формулы, позволяющие делать расчеты при несовпадениях моментов поступления аннуитетных платежей и начисления процентов.
Основные формулы раздела
 (8.1)
(8.1)
 = A× FM4(r,n); (8.2)
= A× FM4(r,n); (8.2)
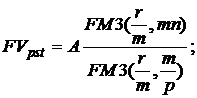 (8.3)
(8.3)
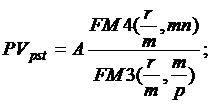 (8.4)
(8.4)
 (8.5)
(8.5)
 (8.6)
(8.6)
 (8.7)
(8.7)
где A – величина каждого денежного поступления;
 – будущая стоимость аннуитета постнумерандо и пренумерандо;
– будущая стоимость аннуитета постнумерандо и пренумерандо;
|
|
|
 – приведенная стоимость аннуитетов постнумерандо и пренумерандо;
– приведенная стоимость аннуитетов постнумерандо и пренумерандо;
r – ставка за базовый период начисления процентов;
p – количество денежных поступлений в периоде;
m – количество начислений сложных процентов в периоде;
n – количество периодов;
h – число периодов, через которое начинает поступать первый из платежей.
Типовые задачи с решениями
Задача 1
Анализируются 2 варианта накопления средств по схеме аннуитета пренумерандо, т.е. поступление денежных средств осуществляется в начале соответствующего временного интервала:
План 1: вносить на депозит 500 долл. каждые полгода при условии, что банк начисляет 10% годовых с полугодовым начислением процентов.
План 2: делать ежегодный вклад в размере 1000 долл. на условиях 9% годовых при ежегодном начислении процентов.
Ответьте на следующие вопросы:
1. Какая сумма будет на счёте через 10 лет при реализации каждого плана? Какой план более предпочтителен?
2. Изменится ли ваш выбор, если процентная ставка в плане 2 будет снижена до 8%?
Решение
План 1:
Принимая за базовый период полгода, воспользуемся формулой (8.5) при n=20; m=1; p=1; r=5%.
FV1=0,5×FM3(5%,20)=0,5×33066=16533$.
План 2:
Принимая за базовый период год, воспользуемся формулой (8.5) при n=10; m=1; p=1; r=9%.
|
|
|
FV2=1×FM3(9%,10)=1×15193=15193$.
В данной задаче более предпочтительным является план 1, так как в этом случае будущая стоимость денежного потока выше. Если процентная ставка в плане 2 будет снижена до 8%, то будущая стоимость денежного потока будет равна:
FV2=1×FM3(8%,10)=1×14487=14487 $,
то и в этом случае решение не изменится, то есть выгоднее план 1.
Задача 2
Вы имеете возможность делать ежеквартально взнос в банк в размере 100 долл. Банк начисляет проценты ежеквартально по ставке 16% годовых. Какая сумма будет на счёте к концу года?
Решение
Для решения данной задачи используем формулу (8.1) при n=4; r=4%; k=4:
FV=A×FM3(4%,4)= 424,6 $.
Задача 3
К моменту выхода на пенсию, т.е. через 8 лет, г-н N хочет иметь на счете 30000 долл. Для этого намерен делать ежегодный взнос по схеме пренумерандо. Определите размер взноса, если банк предлагает 7% годовых.
Решение
Для решения задачи используются формулы (8.1) и (8.5) при n=8; m=1; p=1; r=7%, из которой выражается величина ежегодного взноса:
A = FVapre / (FM3(r,n) (1+r)).
Подставляя в формулу числовые значения и табличные значения FM3(7%,8), получим, что размер ежегодного взноса при ставке 7% годовых составит:
|
|
|
A = 30000 / (10,26(1+0,007)) = 2732,69 $.
Задача 4
Клиент в конце каждого года вкладывает 3 тыс. руб. в банк, выплачивающий сложные проценты по ставке 25% годовых. Определить сумму, которая будет на счете через 7 лет. Если эта сумма получается в результате однократного помещения денег в банк, то какой величины должен быть взнос?
Решение
Для определения суммы, накопленной на счете, используем формулу (8.1) при n=7; r=25%; A=3:
FV=3×FM3(25%,7)=3×15,0735=45221 руб.
Для определения величины однократного взноса в начале первого года, который при наращении сложными процентами через 7 лет станет равным 45221 руб., можно воспользоваться формулами (8.2) или (3.2):
PV=3×FM2(25%,7)=3×3,1611=9483 руб.
PV=FV/(1+0,25)7= 9483 руб.
Задача 5
Предприниматель в результате инвестирования в некоторый проект будет получать в конце каждого квартала 8 тыс. руб. Определить возможные суммы, которые через три года получит предприниматель, если можно поместить деньги в банк под сложную процентную ставку 24% годовых с начислением процентов: а) ежегодно; б) ежеквартально; в) ежемесячно.
Решение
а) используем формулу (8.3) при А=8 тыс. руб., n=3, r=24%, m=1, p=4:
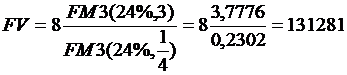 руб., причем значение
руб., причем значение
 вычисляем непосредственно по формуле
вычисляем непосредственно по формуле
|
|
|

б) используем формулу (8.1), считая базовым периодом квартал, тогда n=12, r=6%
FV=8FM3(6%,12)=8×16,8699=134959 руб.
в) используем формулу (8.1) при А=8 тыс. руб., n=3, r=24%, m=12, p=4:
FV=8FM3 (2%,36)/FM3(2%,3)=8(51,9944/3,0606)=135915 руб.
Задача 6
Какую сумму необходимо поместить в банк под сложную процентную ставку 36% годовых, чтобы в течение 6 лет иметь возможность в конце каждого года снимать со счета 8 тыс. руб., исчерпав счет полностью, если банком начисляются сложные проценты: а) ежегодно; б) ежемесячно?
Решение
Для ответа на поставленный вопрос во всех случаях необходимо определить приведенную стоимость аннуитета постнумерандо при А=8 тыс. руб., n=6.
а) полагая r=36%, по формуле (8.2) находим:
PV=8FM4(35%,6)=8×2,3388=18710 тыс. руб.
б) используем формулу (8.4) при m=12, р=1, получим
PV=8FM4(3%,72)/FM3(3%,12)=8(29,3651/14,1920)=16553 тыс. руб.
Задача 7
Банк предлагает ренту постнумерандо на 15 лет с полугодовой выплатой 10 тыс. руб. Годовая процентная ставка в течение всего периода остается постоянной, сложные проценты начисляются по полугодиям. По какой цене можно приобрести эту ренту, если выплаты будут осуществляться: а) через 3 года; б) немедленно, а сложная процентная ставка равна 4% годовых?
Решение
а) используем формулу (8.7), считая полугодие базовым периодом, при h=6:
PV=10×FM2(2%,6)×FM4(2%,30)=10×0,888×22,3965=198881 руб.
б) используем формулу (8.2), считая полугодие базовым периодом:
PV=10×FM4(2%, 30)=10×22,3965=223965 руб.
Задача 8
Работник заключает с фирмой контракт, согласно которому в случае его постоянной работы на фирме до выхода на пенсию (в 65 лет) фирма обязуется перечислять в конце каждого года в течение 25 лет на счет работника в банке одинаковые суммы, которые обеспечат работнику после выхода на пенсию в конце каждого года дополнительные выплаты в размере 8000 руб. в течение 18 лет. Какую сумму ежегодно должна перечислять фирма, если работнику 40 лет и предполагается, что банк гарантирует годовую процентную ставку 20% ?
Решение
Выплаты работнику после выхода на пенсию представляют собой аннуитет постнумерандо с А=8000 руб. и длительностью n=18 лет. Полагая r=20%, по формуле (8.2) найдем приведенную стоимость этого аннуитета:
PV=8000×FM4(20%,18)=8000×4,8122=38497 руб.
Полученная величина – необходимая будущая стоимость ежегодных вкладов фирмы на счет работника. Поэтому размер вклада можно найти из формулы (8.1), полагая FV=38497:
A=38497/FM3(20%,25)=38497/417,9811=81,57 руб.
Таким образом, фирме достаточно перечислять на счет работника 81 руб. 57 коп.
Задача 9
Фирме предложено инвестировать 200 млн. руб. на срок 4 года при условии возврата этой суммы частями (ежегодно по 50 млн. руб.); по истечении четырех лет будет выплачено дополнительное вознаграждение в размере 80 млн. руб. Примет ли она это предложение, если можно депонировать деньги в банк из расчета 18% годовых?
Решение
Для решения этой задачи воспользуемся следующей формулой для определения будущей стоимости 200 млн.руб.
FV=PV(1+r)n.
Таким образом, будущая стоимость 200 млн. руб. будет равна 387,76 млн. руб., если инвестор депонирует эти деньги в банк. Если же он их инвестирует, то фирма получит сумму, рассчитанную по формуле (8.1) с А=50 млн. руб., n=4; r=18% плюс единовременное получение 80 млн. руб.:
FV=50×FM3(18%,4)+80=50×5,2154+80=340,77 млн. руб.
Отсюда видно, что фирме более выгодно инвестировать деньги.
Задача 10
Некоторая фирма хочет создать фонд в размере 350 тыс. руб. С этой целью в конце каждого года фирма предполагает вносить по 60 тыс. руб. в банк под 28% годовых. Найти срок, необходимый для создания фонда, если банк начисляет сложные проценты а) ежегодно; б) по полугодиям.
Решение
а) выразим n из формулы (8.1):

FV=350, A=60, r=28%, поэтому:
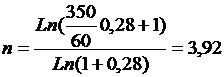 года.
года.
б) найдем срок, подставляя в формулу (8.3) значения всех известных параметров, и выразим n, учитывая, что p=1, m=2:
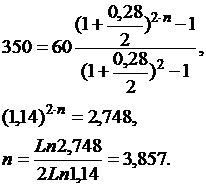
Таким образом, n= 3,857 года.
Дата добавления: 2018-02-15; просмотров: 6287; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
