Тема 5. Эквивалентные и эффективные ставки

Один и тот же финансовый результат можно получить различными способами, используя различные ставки.

Две ставки называются эквивалентными, если при замене одной ставки на другую финансовые отношения сторон не меняются.

Эффективная процентная ставка позволяет сравнивать финансовые операции с различной частотой начисления и неодинаковыми процентными ставками. Именно эта ставка характеризует реальную эффективность операции, однако во многих финансовых контрактах речь чаще всего идет о номинальной ставке, которая в большинстве случаев отличается от эффективной.

Меняя частоту начисления процентов или вид ставки, можно существенно влиять на эффективность операции. В частности, оговоренная в контракте ставка в г % может при определенных условиях вовсе не отражать истинный относительный доход (относительные расходы). Например, 60% годовых при условии ежедневного начисления процентов соответствуют на самом деле 82,1%, начисляемых ежегодно. Отмеченная особенность исключительно значима в условиях высоких номинальных ставок. При составлении финансовых договоров данный прием нередко используется для вуалирования истинных расходов. Поэтому, заключая контракт, целесообразно уточнять, о какой ставке (процентной, учетной, эффективной и др.) идет речь или, по крайней мере, отдавать себе отчет в этом.

Основные формулы раздела

r_e=(1 + r/m)^m – 1; (5.1)

r_e=e^d – 1; (5.2)

(5.3)

(5.4)

(5.5)

(5.6)

(5.7)

где - эффективная ставка,

- сила роста,

r – простая процентная ставка,

d – простая учетная ставка,

r(m) – сложная процентная ставка,

d(m) – сложная процентная ставка,

n – продолжительность финансовой операции в годах,

m1, m2 – количество начислений процентов в году.

Типовые задачи с решениями

Задача 1

Какие условия предоставления кредита и почему более выгодны банку: а) 28% годовых; б) 30% годовых, начисление полугодовое?

Решение

Для решения задачи воспользуемся формулой (5.1).

Рассчитаем эффективную годовую процентную ставку для каждого варианта:

a) r_e = (1 + 0.28/4)⁴ – 1 = 31.1%;

b) r_e = (1 + 0.3/2)² – 1 = 32.25%.

Для банка выгоднее предоставлять кредит по варианту b), так как в этом случае эффективная годовая ставка выше (предоставлять кредит под 32,25% годовых выгоднее, чем под 31,1%).

Задача 2

Рассчитайте эффективную годовую процентную ставку, если номинальная ставка равна 12% и проценты начисляются: а) ежегодно; б) каждые 6 месяцев; в) ежеквартально; г) ежемесячно; д) ежедневно; e) непрерывно.

Решение

Для расчета эффективной годовой ставки воспользуемся формулой (5.1).

При ежегодном начислении процентов r_e = (1 + 0.12) – 1 = 0.12 = 12%.

При полугодовом начислении процентов r_e=(1 + 0.12/2)² – 1 =12,36%.

При ежеквартальном начислении процентов r_e=(1+0.12/4)⁴–1=12,55%.

При ежемесячном начислении процентов r_e=(1+0.12/12)¹²–1=12,68%.

При ежедневном начислении процентов r_e=(1+0.12/360)³⁶⁰–1=12,747%.

При непрерывном начислении процентов воспользуемся формулой: (3.2):

r_e= e^0.12 – 1 = 12.749%.

Задача 3

Какие условия предоставления кредита и почему более выгодны клиенту банка: а) 24% годовых, начисление ежемесячное; б) 26% годовых, начисление полугодовое?

Решение

Для решения задачи воспользуемся формулой эффективной годовой процентной ставки:

r_e=(1 + r/m)^m – 1.

Рассчитаем эффективную годовую процентную ставку для каждого варианта:

а) r_e = (1 + 0.24/12)¹² – 1 = 26,8%;

б) r_e = (1 + 0.26/2)² – 1 = 27,69%.

Для клиента выгоднее брать кредит по варианту а), так как в этом случае эффективная годовая ставка ниже (брать кредит под 26,8% годовых выгоднее, чем под 27,69%).

Задача 4

Господин N собирается поместить на некоторый срок свободные денежные средства либо под сложную процентную ставку 30% годовых с ежеквартальным начислением процентов, либо под простую процентную ставку 48% годовых. Выясните, как выгоднее поступить при сроке: а) 3 года; б) 4 года?

Решение

а) Чтобы сделать правильный выбор, необходимо найти для данной сложной процентной ставки 30% эквивалентную простую процентную ставку и сравнить ее с предлагаемой простой процентной ставкой 48%. Используем формулу (5.3) при n=3, m=4, r(4)=0,3.

Так как r = 46,06% меньше 48%, то выгоднее на три года поместить капитал под простую процентную ставку 48%.

б) Полагая п = 4, т = 4, r = 0,3, получим:

Так как r = 54,52% превышает 48%, то выгоднее на 4 года поместить капитал под сложную ставку.

Задача 5

Долговое обязательство учтено в банке за 9 месяцев до срока погашения по номинальной годовой учетной ставке d(4) = 32%. По какой простой учетной ставке надо произвести учет этого обязательства, чтобы обеспечить банку тот же самый дисконт?

Решение

Полагая в формуле (5.4) n= 0,75,находим:

Таким образом, искомое значение простой учетной ставки составляет 29,51% годовых.

Задача 6

Банком выдан кредит на три месяца под 27% годовых с ежемесячным начислением сложных процентов. Определите величину простой учетной ставки, обеспечивающей такую же величину начисленных процентов.

Решение

По формуле (5.5) при n=0,25, r(12)=0,27 находим требуемую величину простой учетной ставки:

Таким образом, искомое значение простой учетной ставки составляет 25,83% годовых.

Задача 7

Определите сложную годовую учетную ставку с дисконтированием 2 раза в год, которая эквивалентна годовой номинальной процентной ставке 24%: а) с ежеквартальным начислением сложных процентов; б) с полугодовым начислением сложных процентов.

Решение

а) По формуле (5.6) при m1=2, m2=4, r(4) =0,24:

б) при m1 =m2 = 2, г(2) = 0,24 получим:

Задача 8

Определите величину силы роста при начислении непрерывных процентов в течение двух лет, которая эквивалентна: а) простой процентной ставке 26% годовых; б) сложной процентной ставке 26% годовых с ежемесячным начислением процентов.

Решение

Используем формулу (5.7).

а) Полагая n = 2, г = 0,26, находим:

б) При т = 12, r(12)=0,26:

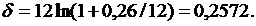
Задача 9

Банк предоставляет ссуду на 25 месяцев под 30% годовых с ежеквартальным начислением процентов по смешанной схеме. Определите эквивалентную годовую простую процентную ставку, обеспечивающую такой же доход банку от предоставления ссуды.

Решение

Покажем, что для данной ситуации нетрудно получить формулу в общем виде. Пусть в течение времени п используется сложная процентная ставка r(m), но при начислении процентов применяется смешанная схема. Тогда множитель наращения имеет вид:

, где w=[mn], f=mn–[mn], n=(w+f)/m.

Множитель наращения при использовании простой процентной ставки имеет вид (1 + nr). Приравнивая эти множители наращения, находим, что эквивалентная простая процентная ставка находится по формуле:

В нашем случае n=35/12 года, m = 4, r(4)=0,3, w=[4·35/12]=[35/3]=11,

f=35/3–11=2/3, поэтому

т.е. эквивалентная простая процентная ставка равна 45,48%.

Таким образом, из полученной выше формулы следует, что простая процентная ставка r эквивалентна по существу двум процентным ставкам: сложной ставке r(m), применяемойзавремя, равное целому числу подпериодов, и простой ставке r(m), применяемой за время, равное дробной части подпериода. При этом если дробная часть подпериода равна нулю (f = 0), то w =[mn], а если целое число подпериодов равно нулю (W = 0), то f/m=n, полученная формула примет вид r=r(m).

Задача 10

Банк принимает вклады до востребования под сложную процентную ставку 20% годовых при временной базе 365 дней. Какую простую годовую учетную ставку должен применить банк при учете векселя за 250 дней до срока его погашения, чтобы обеспечить себе такую же доходность, как и по вкладам до востребования? При учете используется временная база 360 дней.

Решение

Для определения эквивалентной простой годовой учетной ставки нельзя использовать формулу (5.5), так как в ней временные базы ставок одинаковы. Получим необходимую формулу, приравнивая соответствующие множители наращения. Пусть Td и Tr – временные базы соответственно учетной и процентной ставок, тогда из равенства

, получим:

, откуда:

Дата добавления: 2018-02-15; просмотров: 3986; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!