Тема 9. Непрерывный и переменный аннуитеты
Если в течение каждого базового периода денежные поступления происходят очень часто, так что промежутки между последовательными поступлениями представляют собой бесконечно малые величины, то аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью: одно и то же количество денежных единиц в единицу времени.
Аннуитет называется переменным, если его члены различны по величине. Для оценки переменного аннуитета используют, вообще говоря, общие формулы оценки денежного потока.
Если члены аннуитета изменяются в соответствии с некоторыми законами (в частности, образуют арифметическую или геометрическую прогрессию), то общие формулы для определения будущей или приведенной стоимости аннуитета можно упростить.
Чтобы при оценке переменного аннуитета без явно выраженной зависимости между его членами пользоваться стандартными формулами, надо стараться представить этот аннуитет в виде суммы или разности постоянных аннуитетов.
Основные формулы раздела
Оценка непрерывного аннуитета:
(9.1)
(9.2)
Оценка непрерывного аннуитета в случае начисления непрерывных процентов:
(9.3)
(9.4)
Оценка переменного аннуитета постнумерандо, платежи которого образуют арифметическую прогрессию:
|
|
|
(9.5)
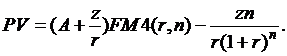(9.6)
Оценка переменного аннуитета постнумерандо, платежи которого образуют геометрическую прогрессию:
(9.7)
(9.8)
Типовые задачи с решениями
Задача 1
В течение 4 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя в сумме 10 тыс. руб. Определите сумму, накопленную к концу четвертого года при использовании процентной ставки 15% годовых, если начисление сложных процентов осуществляется ежегодно.
Решение
Полагаем n =4, т =1, r =15%. Поскольку платежи поступают достаточно часто, будем считать, что они поступают непрерывным образом. Тогда можно воспользоваться формулой (9.1) для определения наращенной суммы непрерывного аннуитета при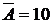 
тыс.руб.
тыс. руб.
Сравним этот результат со значением, полученным по формуле р- срочного аннуитета, предполагая, что в году 360 дней и дан аннуитет постнумерандо. Так как р = 360, А = 10/360, получим:
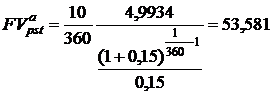тыс. руб.
Видим, что полученные величины отличаются незначительно (всего на 11 руб.).
|
|
|
Задача 2
Фирма намеревается выпускать некоторую продукцию в течение трех лет, получая ежегодно выручку в размере 30 млн. руб. Предполагается, что продукция в течение года будет продаваться более или менее равномерно. Оцените ожидаемые денежные поступления, если применяется непрерывная ставка 20% за год.
Решение
Поскольку в условии говорится о более или менее равномерном распределении продаж в течение года, то логично предполагать, что интенсивность потока выручки будет в какой-то мере постоянной величиной, равной 30 млн руб. в год. Считая, что денежные поступления происходят непрерывно, воспользуемся формулами для определения соответственно будущей и приведенной стоимости непрерывного аннуитета (9.3) и (9.4). Полагая 
млн руб., п = 3, s = 0,2, получим:
млн.руб.
млн.руб.
Задача 3
Финансовая компания в течение пяти лет в соответствии со своими обязательствами должна выплачивать вкладчикам по 20 млн. руб. ежегодно. Какой суммой должна располагать компания, чтобы иметь возможность выполнить обязательства, если норма доходности составляет 30% за год и выплаты происходят постоянно и достаточно равномерно?
Решение
Воспользуемся формулой (9.2) для определения приведенной стоимости непрерывного аннуитета, при 
, n=5, m=1, r=30%:
|
|
|
млн. руб.
Таким образом, имея 55,7 млн. руб., компания способна выполнить свои обязательства перед вкладчиками.
Задача 4
Согласно условиям финансового соглашения на счет в банке в течение 8 лет: а) в конце года; б) в начале года будут поступать денежные суммы, первая из которых равна 4 тыс. руб., а каждая следующая будет увеличиваться на 0,5 тыс. руб. Оцените этот аннуитет, если банк применяет процентную ставку 20% годовых и сложные проценты начисляются один раз в конце года. Как изменятся оценки аннуитета, если денежные суммы будут уменьшаться на 0,5 тыс. руб.?
Решение
а) Согласно условию имеем переменный аннуитет постнумерандо с постоянным абсолютным изменением его членов и, следовательно, для оценки аннуитета воспользуемся формулами вычисления стоимости аннуитета с изменяющейся величиной платежа. По условиям соглашения А =4 тыс. руб., n=8, r =0,2, и если суммы возрастают, то z=0,5 тыс. руб.
Поэтому по формуле (9.5):
тыс. руб.
тыс. руб.
Если суммы будут уменьшаться, то z = –0,5 и, следовательно, по формуле (9.6):
тыс.руб.
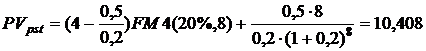тыс.руб.
б) Оценки аннуитета пренумерандо нетрудно получить, используя соотношения:
|
|
|
, поэтому:
если z=0,5, тогда:
FV=87,244×1,2=104693 руб.,
PV=20,29×1,2=24348 руб.
Если z= –0,5, тогда:
FV=44,749×1,2=53699 руб.
PV=10,408×1,2=12490 руб.
Задача 5
За 6 лет необходимо накопить 30 тыс. руб. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 800 руб. и процентная ставка равна 25% годовых? Денежные поступления и начисление сложных процентов осуществляются в конце года. Определите, на какую величину необходимо увеличивать каждый год денежное поступление, если первый вклад будет равен 2 тыс. руб.
Решение
Полагая в формуле (9.5) 
руб., z=0.8 тыс. руб., n=6, r=0, 25, получим уравнение:
30=(А+0,8/0,25)×11,2588–(0,8×6)/0,25,
из которого находим размер первого вклада:
А=1,170 тыс. руб.
Если же известна величина первого вклада А=2 тыс. руб. и неизвестна величина z абсолютного изменения денежных поступлений, то запишем уравнение:
30=(2+z/0,25)×11,2588–(z×6)/0,25, откуда:
z=0,356 тыс. руб.
Задача 6
По условиям контракта на счет в банке поступают в течение 7 лет в конце года платежи. Первый платеж равен 4 тыс. руб., а каждый следующий по отношению к предыдущему увеличивается на 10%. Оцените этот аннуитет, если банк начисляет в конце каждого года сложные проценты из расчета 28% годовых.
Решение
Поскольку ежегодно платежи увеличиваются в 1,1 раза (на 10%), то денежный поток представляет собой переменный аннуитет постнумерандо с постоянным относительным изменением его членов. Поэтому для оценки аннуитетта воспользуемся формулами (9.7) и (9.8). Полагая А = 4 тыс. руб., п = 7, r = 0,28 и q = 1,1, получим:
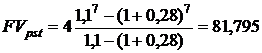тыс.руб.
тыс.руб.
Дата добавления: 2018-02-15; просмотров: 1744; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!