Вопросы, упражнения и задачи к главе «Дифференциальные уравнения»

 

1. Какое уравнение называется дифференциальным? Что называется порядком дифференциального уравнения?

2. Что называется решением дифференциального уравнения?

3. Что определяет уравнение  ?

4. Дайте определение условию Липшица.

5. Сформулируйте теорему Коши.

6. Какое решение дифференциального уравнения называется общим, а какое частным? Каков их геометрический смысл?

7. Какое решение ОДУ называют особым? Каков его геометрический смысл?

8. Какое ОДУ первого порядка называется:

а) с разделяющимися переменными?

б) однородным?

в) линейным?

г) Бернулли?

д) Лагранжа? Клеро?

и как они интегрируются?

9. Что понимается под методом вариации произвольных постоянных (метод Лагранжа)?

10. Какое дифференциальное уравнение второго порядка называется линейным дифференциальным уравнением с постоянными коэффициентами? В каких случаях оно называется однородным и неоднородным?

11. Какова структура общего решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?

12. Как находятся частные решения линейных дифференциальных уравнений второго порядка с постоянными коэффициентами с правой частью специального вида?

13. Как решать системы линейных дифференциальных уравнений?

14. Какая система линейных уравнений называется нормальной?

 

I. Найти общие решения следующих дифференциальных уравнений

1)

2)

3)

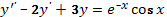
4)

II. Найти частные решения дифференциальных уравнений, удовлетворяющие начальным условиям

     5)

     6)

     7)

III. Решить задачу Коши для следующих систем:

       8)

       9)  

IV. Проинтегрировать систему

       10)

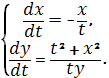
V. Найти общие решения дифференциальных уравнений

       11)

       12)

       13)

VI. Найти частные решения дифференциальных уравнений, удовлетворяющие начальным условиям:

       14)

       15) 

       16)

VII. Найти общие решения следующих дифференциальных уравнений:

       17)

       18)

       19)

       20)

 

 

Ответы.

1.

2. ;

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

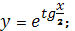
15.

16. 

17.

18.

19.

20.

 

 

 

Тест для самоконтроля к главе «Дифференциальные уравнения»

1. Число особых решений дифференциального уравнения 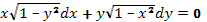 равно

Варианты ответов:

1) 0 (нет особых решений);

2) одно;

3) два;

4) три.

2. Общий интеграл дифференциального уравнения   имеет вид

Варианты ответов:

1) ;

2) ;

3) ;

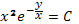4) .

3. Частное решение уравнения 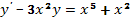, удовлетворяющее начальным условиям  при 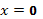  имеет вид

Варианты ответов:

1) ;

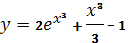2) ;

3) ;

4) .

4. Частное решение уравнения , удовлетворяющее начальным условиям   при 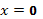  имеет вид

Варианты ответов:

1) ;

2) ;

3) ;

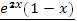4) .

5. Общее решение дифференциального уравнения   имеет вид

Варианты ответов:

1) ;

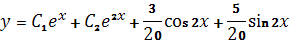2) ;

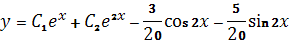3) ;

4)

 

 

---

Дата добавления: 2018-02-15; просмотров: 608; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!