Линейные дифференциальные уравнения высших порядков
1. Линейным дифференциальным уравнением порядка n называется уравнение вида
(34), где 
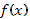- функция независимой переменной х, по которой вычислены производные.
Отличительной чертой линейного уравнения является то, что искомая функция у и все ее производные входят в это уравнение в первой степени.
2. Предполагается, что функции 
и правая часть уравнения – функция 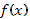непрерывны в промежутке (a, b), случаи 
не исключаются. Функции 
называются коэффициентами уравнения.
3. Задача Коши для этого уравнения при сделанном предположении п.2 всегда имеет единственное решение при любых начальных условиях, лишь бы точка 
находилась в промежутке (a, b) непрерывности функций и .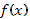
4. Если в уравнении (34) правая часть 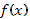тождественно равна нулю в промежутке (a, b), то уравнение (34) примет вид 
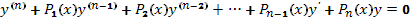(35) и называется в этом случае линейным однородным уравнении. При 
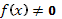уравнение (34) называется неоднородным.
5. Если функция 
является решением линейного однородного уравнения (35), то и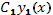 
- произведение ее на произвольную постоянную величину 
- также является решением этого уравнения.
6. Если функции и 
являются решениями линейного однородного уравнения (35), то и их сумма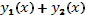 
также является решением этого уравнения. Если функции 
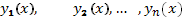являются решениями уравнения (35), то и функция 
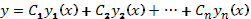, где 
- произвольные постоянные, также является решением этого уравнения. Функции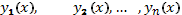 
называются решениями уравнения (35).
|
|
|
7. Две функции и называются линейно независимыми в промежyтке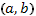 
, если их отношение 
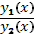в этом промежутке не является постоянной величиной. Если же отношение 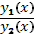- постоянная величина, то эти функции называются линейно зависимыми.
8. Если имеется n функций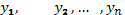 
, то они называются линейно независимыми в промежутке 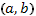при условии, что равенство 
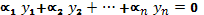(где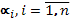 
- постоянные) может выполняться только тогда, когда все коэффициенты 
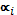равны 0. Если же это равенство в промежутке 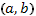имеет место, когда хотя бы один из коэффициентов 
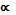не равен 0, то функции называются линейно зависимыми.
9. Если функции 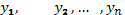являются решениями уравнения (35) и в промежутке 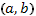они линейно независимы, то общее решение этого уравнения имеет вид:
(36)
Эта формула определяет структуру общего решения линейного однородного уравнения (35) порядка n и указывает способ построения общего решения.
Таким образом, чтобы найти решение линейного однородного уравнения, надо найти n его частных линейно зависимых в 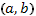решений, каждое из них умножить на произвольную постоянную величину и все эти произведения сложить.
Система линейно независимых решений называется фундаментальной.
10. Для того, чтобы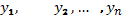 
были линейно независимы в промежутке 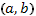, необходимо и достаточно, чтобы их так называемый определитель Вронского был отличен от нуля хотя бы в одной точке 
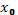промежутка 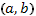, в котором непрерывны коэффициенты уравнения (35)
|
|
|
Таким образом, чтобы проверить линейную независимость функций 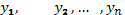надо составить их определитель Вронского 
и убедиться, что хотя бы при одном значении х из промежутка 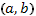он не равен 0.
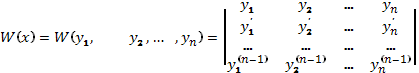
Уравнение (35) имеет n и только n линейно независимых решений.
Если известно частное решение линейного однородного уравнения (35), то его порядок можно понизить на единицу при помощи подстановки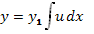 
(*), где 
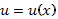- новая искомая функция. Полученное в результате подстановки (*) уравнение также будет линейным.
Дата добавления: 2018-02-15; просмотров: 637; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!