Дифференциальные уравнения в полных дифференциалах
Уравнение вида 
(10) называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции 
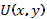, где 
.
Для того, чтобы уравнение (10) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие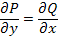 
.
Уравнение (10) есть уравнение в полных дифференциалах, оно может быть записано в виде 
. Общий интеграл этого уравнения, где С – произвольная постоянная.
Функция 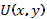может быть найдена следующим образом. Интегрируя равенство 
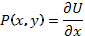по х при фиксированном у и замечая, что произвольная постоянная в этом случае может зависеть от у, имеем:
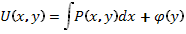(11)
Затем из равенства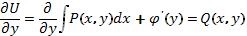 
находим функцию 
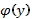, подставив которую в (11) получаем функцию .
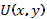Для записи общего (решения) интеграла исходного уравнения достаточно выбрать одну из функций получаемого семейства.
Замечание 7. Более простой метод отыскания функции 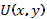состоит в вычислении так называемого криволинейного интеграла второго рода
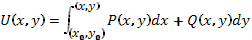
Где точк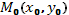и 
и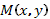 
и путь интегрирования лежат в области непрерывности функций 
и 
и их частных производных, причем, 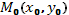- некоторая фиксированная точка.
Пример 8.
, т.е. уравнение в полных дифференциалах.
Следовательно, левая часть уравнения есть полный дифференциал некоторой функции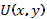
Проинтегрируем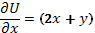 
по х =>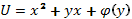 
Найдем произвольную функцию 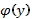, продифференцировав последнее выражение по у
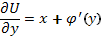, получаем уравнение:
|
|
|
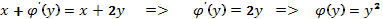
Таким образом, общий интеграл нашего уравнения имеет вид:
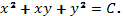
Уравнения, не разрешенные относительно производной
Обыкновенное дифференциальное уравнение (ОДУ) первого порядка, не разрешенное относительно производной, имеет вид: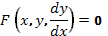 
(12)
Допустим, ОДУ (12) можно разрешить относительно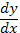 
(пусть и неоднозначно), т.е. можно получить r соотношений 
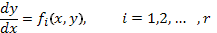(13)
Тогда к каждому из r ОДУ (13) можно применять методы интегрирования, изложенные выше.
Но приведение к виду (13) не всегда возможно. Поэтому решение ОДУ (12) часто приходится искать, используя параметр, например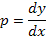 
.
Рассмотрим ряд частных случаев.
Предположим, что (12) можно разрешить относительно у, т.е. записать в виде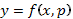 
. Вычислим полный дифференциал 
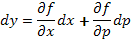. Поскольку 
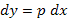, то его можно представить в виде ОДУ 
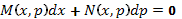, интегрируя которое (если это возможно), найдем общее решение 
. Тогда общее решение исходного ОДУ (12) в параметрической форме будет иметь вид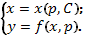 
Пример 9. В уравнении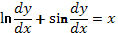 
положим 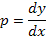и запишем 
.
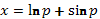Так как 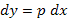, то имеем 
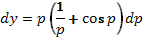и интегрируя, получаем общее решение исходного ОДУ в параметрической форме:
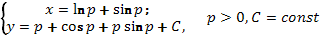
Рассмотренным методом решают, в частности, уравнения Лагранжа и Клеро.
Уравнением Лагранжа называют ОДУ вида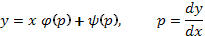 
(14), где 
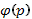и 
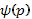- непрерывно дифференцируемые функции, 
.
|
|
|
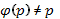Поскольку 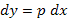и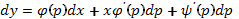 
, то можно записать
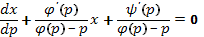(15)
Так как ОДУ (15) линейно относительно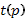 
, то его можно проинтегрировать по р. После интегрирования получим .
Подставив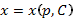 
в (14), запишем общее решение уравнения Лагранжа в параметрической форме: 
.
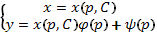Пример 10. Рассмотрим ОДУ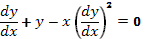 
Это уравнение Лагранжа. Обозначим 
Тогда ОДУ (15) примет вид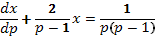 
Решая его, получим
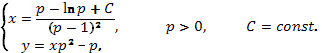
Частным случаем уравнения Лагранжа является уравнение Клеро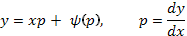 
(16), названное по имени французского математика и астронома А.К. Клеро (1713-1765).
Применим ту же процедуру, что и при решении уравнения Лагранжа:
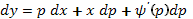, а так как 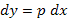, то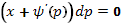 
, т.е. либо 
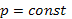, либо 
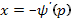. В первом случае в соответствии с (16) имеем общее решение уравнения Клеро в виде 
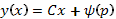, а во втором – особое решение этого ОДУ в параметрической форме:
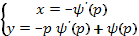
Действительно, касательная к интегральной кривой (16) в точке, соответствующей фиксированному значению параметра р, имеет уравнение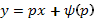 
, т.е. входит в семейство прямых, задаваемых решением 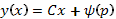, причем угловой коэффициент касательной в этой точке, согласно правилу дифференцирования функции, заданной параметрически, равен
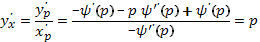
Вместе с тем при значении параметра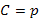 
эта точка лежит на прямой 
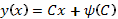, так и на интегральной кривой (16). Следовательно, решение (16) особое, а интегральная кривая является огибающей однопараметрического семейства прямых .
|
|
|
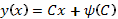Пример 11. Решим уравнение Клеро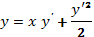 
.
Здесь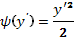 
. Согласно изложенному выше, общим решением этого ОДУ будет 
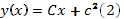, а (16) задает особое решение, причем 
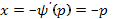, а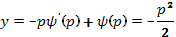 
.
Таким образом, особое решение исходного ОДУ принимает вид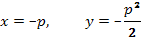 
или, после исключения р, 
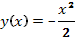, т.е. интегральная кривая особого решения как огибающая семейства прямых 
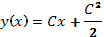будет параболой (рис. 3).
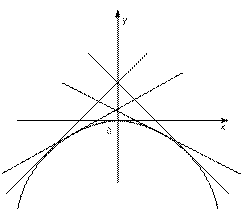
Рис. 3.
(последнее будет обосновано после формулировки варианта теоремы Коши существования и единственности решения ОДУ первого порядка, но вида (12), т.е. ОДУ, не разрешенного относительно производной).
Теорема 2. (Теорема Коши)
Пусть функция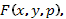 
где 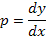, в окрестности точки 
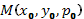непрерывна по всем переменным и непрерывно дифференцируема по у и р. Пусть, кроме того, 
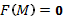и в точке М 
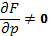. Тогда существует единственное решение 
задачи Коши для ОДУ (12), удовлетворяющее начальному условию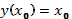 
.
Из этой теоремы следует, что особое решение ОДУ (12), если таковые существуют, удовлетворяют системе уравнений:
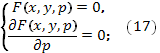
Для отыскания особого решения необходимо из системы (17) исключить р. Полученное после этого соотношение определяет так называемую дискриминантную кривую. Каждую ветвь этой кривой необходимо проверить, чтобы узнать, соответствует ли она решению ОДУ (12), и если соответствует, то это решение, вообще говоря, особое.
|
|
|
Для уравнения Клеро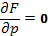 
при 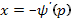, и система (17) дает решение (16), которое является особым.
Дата добавления: 2018-02-15; просмотров: 756; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!