Дифференциальные уравнения с разделяющимися переменными

Глава 12. Элементы теории обыкновенных дифференциальных уравнений (ОДУ)

Дифференциальные уравнения занимают особое место в математике и имеют многочисленные приложения в большом спектре наук. Исследования природных процессов и изучение закономерностей общественных процессов приводят к построению математических моделей, основой которых являются дифференциальные уравнения.

В дифференциальных уравнениях неизвестная функция содержится вместе со своими производными. Основной задачей теории дифференциальных уравнений является изучение функций, представляющих собой решение этих уравнений. В этой главе излагаются элементы теории обыкновенных дифференциальных уравнений (ОДУ), когда неизвестные функции зависят от одной переменной. Теория дифференциальных уравнений, когда известные функции зависят от нескольких переменных – уравнения в частных производных, является более сложной и представляет специальный раздел математики.

Простейшие обыкновенные дифференциальные уравнения рассматривал в своих работах еще И.Ньютон и Г.Лейбниц. Именно Г.Лейбниц ввел в 1676г. термин «дифференциальное уравнение». Задачу решения ОДУ И.Ньютон трактовал как обратную по отношению к нахождению производной для заданной функции, а вычисление неопределенного интеграла он считал частным случаем этой задачи.

Для Ньютона как создателя основ математического естествознания такой подход к восстановлению функции по зависимости между функцией и ее производными был вполне логичным, поскольку большинство известных в науке закономерностей может быть выражено в форме дифференциальных уравнений.

Основные понятия и определения

Опр.1. Дифференциальным уравнением называется соотношение, связывающее независимую переменную, неизвестную функцию или ее производную (или ее дифференциал).

В случае, когда неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, дифференциальное уравнение называется обыкновенным.

Обыкновенное дифференциальное уравнение первого порядка имеет вид (*), а если его удается решить относительно производной, то оно запишется так: (1) .

Решением или интегралом уравнения (1) называется всякая дифференциальная функция , удовлетворяющая этому уравнению, т.е. такая, после подстановки в которой в уравнение (1) оно обращается в тождество, т.е. является тождеством относительно x.

Кривая , определяемая решением уравнения (*) или (1) называется интегральной кривой дифференциального уравнения.

Общим решением дифференциального уравнения (*) или (1) называется соотношение вида или (2), включающее одну произвольную постоянную величину и обладающее тем свойством, что решая их относительно у при любых частных значениях произвольной постоянной, получаем функции вида , являющаяся решениями уравнений (*) или (1). Уравнение (2) определяют свойство интегральных кривых (*).

Частным решением дифференциального уравнения (*) называется такое решение, которое получается из общего решения (2) при некотором частном значении произвольной постоянной. Произвольная постоянная С, входящая в (2) определяется из так называемых начальных условий.

Задача с начальными условиями ставится так:

Найти решение уравнения (*) такое, чтобы оно принимало заданное значение при заданном значении независимой переменной , т.е. выполнялось тождество .

С точки зрения геометрии задача с начальными условиями сводится к тому, чтобы из семейства интегральных кривых (2) выделить ту, которая проходит через точку плоскости.

Задача Коши.Задача отыскания решения уравнения (*), удовлетворяющего начальным условиям при называется задачей Коши.

Возникает естественный вопрос о существовании решения задачи Коши и его единственности. Ответ на поставленные вопросы дает одна из центральных теорем в теории ОДУ – теорема Коши, которую мы сформулируем (без доказательства) далее.

Опр.2. Функция , определенная в области G удовлетворяет условию Липшица в G относительно у, если существует такое число L>0, называемое постоянной Липшица, что для любых двух точек (х,у) и (х, t) из G выполнены неравенства .

Замечание 1. Функция , имеющая в замкнутой ограниченной области G непрерывную частную производную , удовлетворяет условию Липшица.

Теорема 1. (теорема Коши)

Пусть функция определена и непрерывна в прямоугольной замкнутой области удовлетворяет в этой области условию Липшица относительно у. Тогда существует единственное решение задачи Коши, т.е. решение обыкновенного дифференциального уравнения (ОДУ) первого порядка с начальным условием .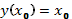

Это решение определено при , где ,

Рис. 1.

Дадим геометрическую интерпретацию ограничения на область определения функции . Так как , то интегральная кривая , проходящая через точку , должна лежать внутри заштрихованного на рис.1 участке области D и не может пересекать прямые, описываемые уравнениями (иначе в окрестностях точки пересечения было бы ), что противоречит ОДУ (1). Если 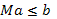, то казанные прямые пересекают границу области D в угле прямоугольника или по его вертикальным сторонам, а интегральная кривая гарантированно определена при , т.е. . Если же 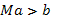(как изображено на рис.1), то точки пересечения прямых с границей области D лежат на горизонтальных сторонах прямоугольника и имеют абсциссы . В этом случае интегральная кривая гарантированно определена лишь при .

Если в обыкновенном дифференциальном уравнении (ОДУ) первого порядка правая часть непрерывна в некоторой области D и удовлетворяет условию Липшица по у, то через каждую точку этой области проходит, согласно теореме Коши, единственная интегральная кривая. Такую точку интегральной кривой называют обыкновенной. Точку , не являющуюся обыкновенной, называют особой точкой ОДУ . Через особую, точку вообще говоря, не проходит ни одна интегральная кривая или же проходят по крайней мере две интегральные кривые.

Нарушение условий теоремы Коши в точке является лишь необходимым условием того, что эта точка является особой. Например, для ОДУ точка будет особой, поскольку через нее проходят бесконечное множество интегральных кривых , где С – произвольная постоянная. Напротив, через особую точку ОДУ не проходит ни одной интегральной кривой .

Особым решением ОДУ называется такое решение ОДУ (1), которое во всех своих точках не удовлетворяет свойству единственности, т.е. в окрестности каждой точки 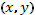особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Теорема Коши дает достаточные условия для того, чтобы в некоторой области не существовали особые решения. Таким образом, для существования последних необходимо, чтобы условия этой теоремы были нарушены. Если, например, непрерывна в некоторой области, то особые решения могут проходить только через те точки, в которых не выполнено условие Липшица.

Пусть задано уравнение , определяющее на плоскости некоторое семейство кривых, зависящих от параметра С. Если составить систему двух уравнений и , то, исключая из этой системы параметр С, получим, вообще говоря, дифференциальное уравнение заданного семейства кривых.

Пример 1. Рассмотрим ОДУ . Интегрируем его, находим общее решение (рис.2). Кроме того, это ОДУ имеет особое решение , проходящее через точки, где не выполнено условие Липшица (см. рис.2). Действительно, если бы условие Липшица было выполнено для кривой части этого ОДУ, то при было бы справедливо неравенство , где L – постоянная Липшица, но при и левая часть этого неравенства стремится к бесконечности.

Рис. 2.

Пример 2. Найти дифференциальное уравнение семейства окружностей .

Имеем систему уравнений

Исключаем параметр а. Из второго уравнения находим и, подставляя это выражение в первое уравнение, получаем , т.е. . Это и есть искомое дифференциальное уравнение.

Далее рассматриваются специальные виды ОДУ первого порядка, решения которых удается найти в квадратурах. Предполагается, что обсуждаемые ОДУ удовлетворяют условиям теоремы Коши.

Если общее решение (общий интеграл) представлено в виде квадратур от элементарных функций, входящих в состав дифференциального уравнения, то говорят, что уравнение проинтегрировано в квадратурах.

Выясняя вопрос об интегрируемости данного дифференциального уравнения в квадратурах, нужно рассмотреть все формы записи этого уравнения, принимая за искомую функцию как у, так и х.

В случае, когда в точке правая часть уравнения обращается в бесконечность, рассматривают перевернутое уравнение и ищут интегральную кривую, проходящую через эту точку, в виде .

Вообще решение задачи Коши для уравнения в любой из форм его записи ищут в том виде, в каком это оказывается наиболее удобно, т.е. в виде , , или в параметрической форме .

В следующих параграфах рассматриваются уравнения, интегрируемые в элементарных функциях или квадратурах. При этом мы ограничиваемся в большинстве случаев формальным интегрированием, в частности, не всегда указываем область задания общего решения.

Если данное уравнение не интегрируется в квадратурах или выполнение квадратур затруднительно, решение задачи Коши обычно находят методом последовательных приближений или при помощи степенных рядов.

Дифференциальные уравнения с разделяющимися переменными

Если в дифференциальное уравнение первого порядка производная входит в первой степени, то после решения его относительно получаем уравнение вида .

Так как , то уравнение может быть переписано так . В частном случае, когда каждая из функций и 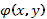является произведением двух функций, одна из которых – функция только х, а вторая только у, т.е. (3). Уравнение (3) называют уравнением с разделяющими переменными. Разделение переменных производится делением обеих частей (3) на произведение , в котором - функция только от у, являющаяся множителем при dx, а - функция только от х, являющаяся множителем при dy.

После деления на это произведение уравнение (3) примет вид (4), а его общий интеграл запишется так (5).

Особые решения с разделяющимися переменными.

Уравнение (5) может быть переписано так

Поэтому, кроме найденного ранее общего интеграла (5) уравнения (3) ему могут также удовлетворять решения, получаемые из уравнения .

Если эти решения не входят в общий интеграл, то они и будут особыми решениями уравнения (3).

Особое решение.Решение дифференциального уравнения, которое не может быть получено из общего решения ни при одном частном значении произвольной постоянной, включая ± называется его особым решением.

При решении дифференциального уравнения надо стремиться к тому, чтобы наряду с определением общего решения были найдены также и особые.

Замечание 2. С помощью подстановки к уравнениям с разделяющимися переменными приводятся и дифференциальные уравнения вида (•),

Уравнение (•) примет вид: , , или .

Пример 3. Решить дифференциальное уравнение.

Разделим обе части на .

=> берем интегралы обеих частей 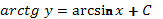=> . В нашей задаче является особым решением (оно не может быть получено из общего интеграла ни при одном частном значении произвольной постоянной С).

Дата добавления: 2018-02-15; просмотров: 1337; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!