Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
С линейными системами дифференциальных уравнений второго порядка приходится встречаться часто в теоретической механике, сопротивлении материалов и в других приложениях математики.
Система дифференциальных уравнений, разрешенных относительно наивысших производных искомых функций, называется канонической.
В случае трех неизвестных функций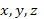 
и независимой переменной 
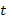эта система уравнений записывается так:
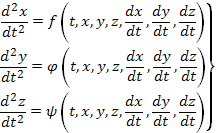(62)
Общее решение этой системы содержит шесть произвольных постоянных, для определения которых задается шесть начальных условий (в механике это начальное положение и скорость точки в некоторый момент времени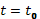 
).
Для определения решения канонической системы (62) применяется такой же прием, как и при решении рассмотренных выше нормальных систем: последовательным дифференцированием одного уравнения системы (или нескольких ее уравнений) следует исключить все искомые функции, кроме одной.
Сущность этого приема подробно разберем на примере.
Пример 20. Найти общее решение системы уравнений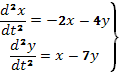 
Решение: Продифференцируем первое уравнение два раза по 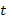и получим
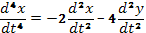(63)
Подставим в (63) вместо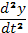 
его выражение из второго уравнения системы.
Тогда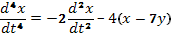 
, или 
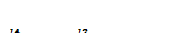(64)
Из первого уравнения системы определим 
и подставим его в уравнение (64)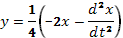 
(65)
C этим значением уравнение (64) перепишется так: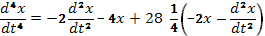 
, раскрывая скобки, получим 
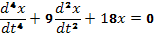. Характеристическое уравнение 
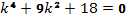имеет корни 
|
|
|
Функция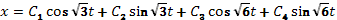 
(66)
Теперь из (65) найдем у, из (66) находим
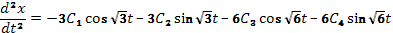
Подставляя х и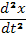 
в (65), получаем
.
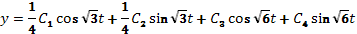Понятие решения
Постановка задачи. Доказать, что функция 
удовлетворяет дифференциальному уравнению 
.
Алгоритм решения.
Для доказательства того, что функция удовлетворяет уравнению , достаточно вычислить производную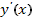 
, подставить 
и 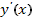в это уравнение и убедиться в том, что получается тождество, т.е. 
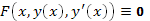для всех допустимых х.
Пример 21. Доказать, что функция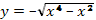 
удовлетворяет уравнению 
.
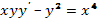Решение. Имеем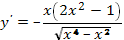 
.
Подставим и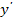 
в левую часть уравнения и проведем необходимые преобразования:
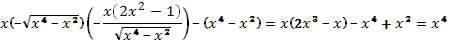
Получаем тождество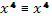 
.
Ответ. Функция 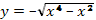удовлетворяет заданному уравнению.
Условия задач. Доказать, что функция удовлетворяет дифференциальному уравнению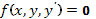 
.
1. 
.
. 
.
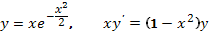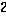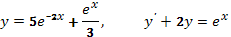Уравнения с разделяющимися коэффициентами
Постановка задачи. Найти интегральные кривые дифференциального уравнения вида
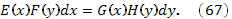
Алгоритм решения.
1. В области, где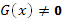 
и 
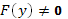разделяем переменные, т.е. представляем уравнение (67) в виде
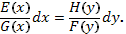
2. Вычислим интегралы в уравнении
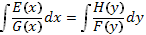
и преобразуем его к виду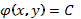 
.
3. Ответ записываем в таком виде: интегральные кривые определяются уравнением 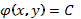при всех возможных значениях С.
|
|
|
Замечание 11. Если одно или оба уравнения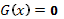 
и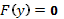 
имеют решения 
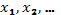и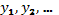 
, то равенства 
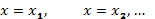и 
нужно присоединить к ответу, так как они являются интегральными кривыми дифференциального уравнения (67).
Пример 22. Найти интегральные кривые дифференциального уравнения
Решение.
1. Перепишем исходное уравнение в виде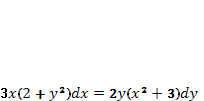 
. (68)
Поскольку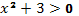 
и 
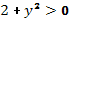, разделяем переменные, т.е. представляем уравнение (68) в виде
2. Вычислим интегралы в уравнении
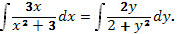
Имеем
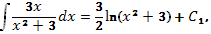
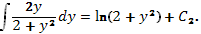
Следовательно, , где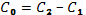 
.
3. Упростив это равенство, получим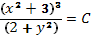 
.
Ответ. Интегральные кривые определяются уравнением
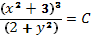
при всевозможных значениях С.
Условия задач. Найти интегральные кривые дифференциальных уравнений.
1. 
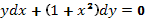. Ответ: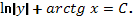 
2. 
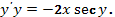Ответ: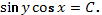 
Однородные уравнения
Постановка задачи. Найти интегральные кривые однородного дифференциального уравнения первого порядка, т.е. дифференциального уравнения вида
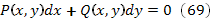
где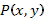 
и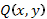 
- однородные функции одинакового порядка, т.е. 
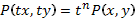и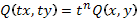 
.
Алгоритм решения.
1. Преобразуем уравнение (69) к виду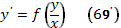 
2. Делаем подстановку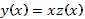 
, где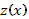 
- новая неизвестная функция. Тогда 
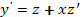и уравнение (69’) приводится к виду
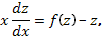
т.е. к уравнению с разделяющимися переменными.
|
|
|
Заметим, что подстановку 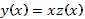можно делать сразу в уравнении (69), не приводя его к виду (69’).
3. Разделяем переменные в области, где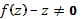 
:
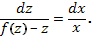
4. Интегрируем полученное уравнение с разделенными переменными и делаем замену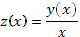 
. Записываем ответ.
Замечание 12. Если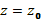 
- корень уравнения 
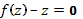, то решением уравнения (69) будет также 
.
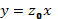Замечание 13. Интегральные кривые однородного уравнения можно искать и в полярных координатах.
Пример 23. Найти интегральные кривые дифференциального уравнения
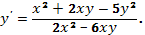
Решение.
1. Преобразуем заданное уравнение к виду
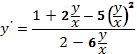
(мы разделили числитель и знаменатель правой части заданного уравнения на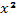 
).
2. Делаем подстановку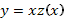 
, где 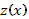– новая неизвестная функция. Тогда 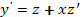и уравнение приводится к виду
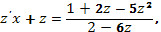
т.е. к уравнению с разделяющимися переменными.
В результате простых преобразований получаем
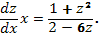
3. Разделяем переменные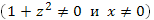 
:
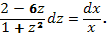
4. Интегрируя, получаем
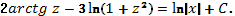
Заменяя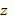 
на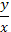 
, получаем
Ответ. Интегральные кривые определяются уравнением
при всех возможных значениях С.
Условия задач. Найти интегральные кривые дифференциальных уравнений.
1. 
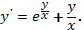Ответ: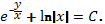 
2. 
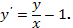Ответ: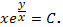 
|
|
|
Дата добавления: 2018-02-15; просмотров: 4115; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!