Линейные уравнения с постоянными коэффициентами
Постановка задачи. Найти общее решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами

где  - многочлен степени
- многочлен степени 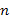 ,
, 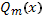 - многочлен степени
- многочлен степени 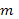 и
и 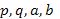 - действительные числа.
- действительные числа.
Алгоритм решения.
Общее решение неоднородного линейного уравнения -го порядка имеет следующую структуру:

где  – фундаментальная система решений и
– фундаментальная система решений и  - общее решение соответствующего однородного уравнения,
- общее решение соответствующего однородного уравнения,  - какое-нибудь частное решение неоднородного уравнения.
- какое-нибудь частное решение неоднородного уравнения.
1. Записываем соответствующее однородное уравнение

и ищем его решение в виде 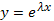 , где
, где  - неизвестное число.
- неизвестное число.
Подставляя  и
и  в уравнение (91) и сокращая
в уравнение (91) и сокращая  , получаем так называемое характеристическое уравнение
, получаем так называемое характеристическое уравнение

2. Решаем характеристическое уравнение. Обозначим корни характеристического уравнения 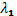 и
и  . Тогда фундаментальная система решений и общее решение уравнения (91) записываются в одном из следующих трех видов:
. Тогда фундаментальная система решений и общее решение уравнения (91) записываются в одном из следующих трех видов:
а) если 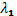 и
и  вещественны и
вещественны и  , то фундаментальная система решений – это
, то фундаментальная система решений – это  и общее решение имеет вид
и общее решение имеет вид
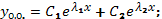
б) если 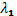 и
и  вещественны и
вещественны и  , то фундаментальная система решений – это
, то фундаментальная система решений – это  и общее решение имеет вид
и общее решение имеет вид

в) если 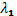 и
и  комплексные, т.е.
комплексные, т.е.  , то фундаментальная система решений – это
, то фундаментальная система решений – это  и общее решение имеет вид
и общее решение имеет вид

3. Ищем какое-либо частное решение неоднородного уравнения. Поскольку правая часть уравнения имеет вид

можно применить метод подбора частных решений:
если  не является корнем характеристического уравнения (92), то
не является корнем характеристического уравнения (92), то

где  и
и  - многочлены степени
- многочлены степени  с неопределенными коэффициентами;
с неопределенными коэффициентами;
если  есть корень характеристического уравнения (92) кратности
есть корень характеристического уравнения (92) кратности  , то
, то

где  и
и  - многочлены степени
- многочлены степени  с неопределенными коэффициентами.
с неопределенными коэффициентами.
4. Находим неопределенные коэффициенты, подставляя  в исходное уравнение.
в исходное уравнение.
Записываем ответ по формуле (90).
Замечание 15. Аналогично решаются линейные дифференциальные уравнения с постоянными коэффициентами любого порядка.
Пример 29. Найти общее решение линейного дифференциального уравнения

Решение.
1. Записываем соответствующее однородное уравнение

и ищем его решение в виде 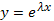 , где
, где  - неизвестное число.
- неизвестное число.
Подставляя  и
и  в уравнение (95) и сокращая
в уравнение (95) и сокращая  , получаем так называемое характеристическое уравнение
, получаем так называемое характеристическое уравнение

2. Характеристическое уравнение имеет два комплексно сопряженных корня  .
.
Имеем фундаментальную систему решений

и общее решение однородного уравнения (95)

3. Ищем какое-либо частное решение неоднородного уравнения (94). В нашем случае правая часть неоднородного уравнения имеет вид (93) с  .
.
Так как характеристическое уравнение имеем комплексные корни  кратности
кратности 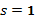 и
и 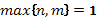 , то частное решение ищем в виде
, то частное решение ищем в виде

где 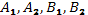 - неизвестные числа (неопределенные коэффициенты).
- неизвестные числа (неопределенные коэффициенты).
4. Находим неопределенные коэффициенты, дифференцируя  два раза и подставляя в уравнение (94).
два раза и подставляя в уравнение (94).
Приравнивая коэффициенты в обеих частях равенства при  , получим четыре уравнения
, получим четыре уравнения
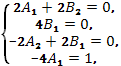
из которых определяем  . Таким образом,
. Таким образом,

По формуле (90) находим общее решение неоднородного уравнения
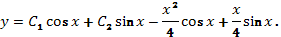
Ответ. 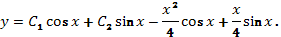
Условия задач. Найти общие решения дифференциальных уравнений.
1.  Ответ:
Ответ: 
2. 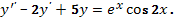 Ответ:
Ответ: 
Принцип суперпозиции
Постановка задачи. Найти общее решение линейного дифференциального уравнения -го порядка с постоянными коэффициентами

где  .
.
Алгоритм решения.
Принцип суперпозиции. Если правая часть уравнения (96) есть сумма нескольких функций  и
и  - какое-нибудь частное решение каздого уравнения
- какое-нибудь частное решение каздого уравнения

то в силу линейности уравнения (96) его общее решение имеет вид

где  - общее решение однородного уравнения
- общее решение однородного уравнения

1. Находим фундаментальную систему решений и общее решение  однородного уравнения.
однородного уравнения.
2. Для каждого неоднородного уравнения (97)  находим частное решение
находим частное решение  (используя, например, метод подбора или метод вариации произвольных постоянных).
(используя, например, метод подбора или метод вариации произвольных постоянных).
Записываем ответ в виде (98).
Пример 30. Найти общее решение линейного дифференциального уравнения
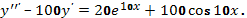
Решение.
1. Записываем соответствующее однородное уравнение

и ищем его решение в виде 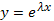 , где
, где  - неизвестное число.
- неизвестное число.
Подставляя  и
и  в уравнение (99) и сокращая
в уравнение (99) и сокращая  , получаем так называемое характеристическое уравнение
, получаем так называемое характеристическое уравнение

Характеристическое уравнение имеет три корня  и
и  .
.
Таким образом, имеем фундаментальную систему решений

и общее решение однородного уравнения

2. Решаем неоднородное уравнение, используя принцип суперпозиции:
а) ищем частное решение  неоднородного уравнения
неоднородного уравнения

в виде  , где А – неопределенный коэффициент ( так как
, где А – неопределенный коэффициент ( так как 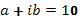 – корень характеристического уравнения кратности
– корень характеристического уравнения кратности 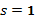 ).
).
Дифференцируя  три раза и подставляя в уравнение (100), находим
три раза и подставляя в уравнение (100), находим  . Таким образом,
. Таким образом,
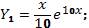
б) ищем частное решение 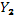 неоднородного уравнения
неоднородного уравнения

в виде  , где
, где  и
и  – неопределенные коэффициенты (так как
– неопределенные коэффициенты (так как  не являются корнями характеристического уравнения, то множитель х отсутствует).
не являются корнями характеристического уравнения, то множитель х отсутствует).
Дифференцируя 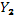 три раза и подставляя в уравнение (101), находим
три раза и подставляя в уравнение (101), находим 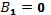 и
и  . Таким образом,
. Таким образом,
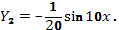
Используя принцип суперпозиции (98), получаем

Ответ.  .
.
Условия задач. Найти общее решение дифференциальных уравнений.
1.  Ответ:
Ответ: 
2.  Ответ:
Ответ: 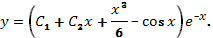
Метод Лагранжа
Постановка задачи. Найти решение задачи Коши для линейного неоднородного уравнения с постоянными коэффициентами

с начальными условиями

Алгоритм решения.
1. Записываем соответствующее однородное уравнение с постоянными коэффициентами

Находим фундаментальную систему решений  и
и  и общее решение однородного уравнения
и общее решение однородного уравнения

2. Применяем метод Лагранжа (метод вариации произвольных постоянных).
Если известна фундаментальная система решений  и
и  однородного уравнения (103), то общее решение соответствующего неоднородного уравнения (102) может быть найдено по формуле
однородного уравнения (103), то общее решение соответствующего неоднородного уравнения (102) может быть найдено по формуле
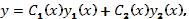
где функции  и
и 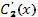 определяются из системы линейных алгебраических уравнений
определяются из системы линейных алгебраических уравнений

Интегрируя, находим функции  и
и  и записываем общее решение неоднородного уравнения.
и записываем общее решение неоднородного уравнения.
3. используя начальные условия (102’), находим решение задачи Коши.
Записываем ответ в виде  .
.
Пример 31. Найти решение задачи Коши

с начальными условиями  .
.
Решение.
1. Записываем соответствующее однородное уравнение:

Находим фундаментальную систему решений  и
и  и общее решение однородного уравнения
и общее решение однородного уравнения
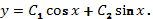
2. применяем метод Лагранжа (метод вариации произвольных постоянных):
а) ищем решение данного неоднородного уравнения в виде

б) записываем систему уравнений для определения функций :

Решая ее (так как решение ищем в окрестности точки 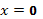 , то
, то  ), получим
), получим

Интегрируя, находим

в) записываем полученное общее решение данного неоднородного уравнения

3. используя начальные условия, определяем константы  и
и 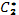 .
.
Так как

то  . Так как
. Так как

то  .
.
Ответ. 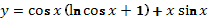 ю
ю
Условия задач. Найти решения задач Коши для дифференциальных уравнений.
1.  Ответ:
Ответ: 
2. 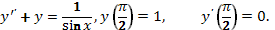 Ответ:
Ответ: 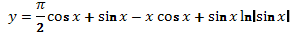 .
.
Дата добавления: 2018-02-15; просмотров: 585; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
