Линейные уравнения первого порядка

⇐ ПредыдущаяСтр 10 из 13Следующая ⇒

Постановка задачи. Решить задачу Коши для уравнения

с начальным условием (70’).

Алгоритм решения.

1-й способ.

1. Запишем соответствующее однородное линейное уравнение:

Это уравнение в разделяющимися переменными.

2. Разделяя переменные и интегрируя, получим общее решение однородного уравнения (71)

3. Применяем метод вариации произвольной постоянной:

а) ищем решение неоднородного уравнения (70) в виде (72), считая С неизвестной функцией х, т.е. полагая .

б) подставляем в уравнение (70) и , определяемые из соотношения (72), где . Из полученного дифференциального уравнения определяем функцию .

4. Таким образом, общее решение неоднородного уравнения (70) получаем в виде

Здесь содержит произвольную постоянную .

5. используя начальные условия (70’), находим значение и получаем решение поставленной задачи Коши.

Записываем ответ в виде .

2-й способ.

1. Ищем решение уравнения (70) в виде

где и - неизвестные функции х.

2. Уравнение (70) принимает вид

3. Поскольку теперь мы имеем две неизвестные функции, а уравнение, которому они должны удовлетворять, только одно, то еще одно уравнение мы можем принять произвольно, лишь бы оно не сужало множество решений у.

Пусть одна из функций (например, ) удовлетворяет уравнению

Тогда уравнение (74) примет вид

Решая уравнение (75) (с разделяющимися переменными), находим , не равное тождественно нулю, чтобы не сужать множество решений у.

4. Подставляем в уравнение (76) и решаем его относительно .

5. Записываем общее решение уравнения в виде.

6. используя начальные условия (70’), получаем решение поставленной задачи Коши.

Записываем ответ в виде .

Пример 24. Найти решение задачи Коши для уравнения

с начальным условием .

Решение.

1-й способ.

1. Записываем соответствующее однородное уравнение

Это уравнение с разделяющимися переменными.

2. разделяя переменные и интегрируя, получаем общее решение однородного уравнения

3. Применяем метод вариации произвольной постоянной:

а) ищем решение неоднородного уравнения (77) в виде

где - неизвестная функция х;

б) подставляя в уравнение (77)

получаем дифференциальное уравнение относительно

Это уравнение с разделяющимися переменными.

Разделяя переменные

и интегрируя, получаем

где - произвольная постоянная.

4. Таким образом, общее решение неоднородного уравнения (77) имеет вид

5. Используя начальное условие , получаем

находим и подставляем в общее решение (78).

Ответ. .

2-й способ.

1. ищем решение уравнения (77) в виде

где и - неизвестные функции х.

2. Уравнение (77) принимает вид

Пусть одна из функций (например, ) удовлетворяет уравнению

Тогда уравнение (79) принимает вид

Решая уравнение (80) (с разделяющимися переменными), находим

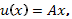
где А – произвольная постоянная ( , чтобы не сужать множество решений).

4. Подставляем в уравнение (81) и решаем его относительно :

где В – произвольная постоянная.

5. Записываем общее решение уравнения (77) в виде

где - произвольная постоянная.

6. Используя начальное условие , находим .

Ответ. .

Условия задач. Найти решения задач Коши для дифференциальных уравнений.

1. . Ответ: .

2. 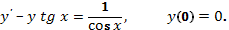Ответ:

Уравнение Бернулли

Постановка задачи. Найти решение задачи Коши для уравнения Бернулли

с начальным условием (82’)

Алгоритм решения.

1. С помощью подстановки

уравнение приводится к линейному

где и .

2. Решаем линейное уравнение (83) и делаем замену .

3. Используя начальное условие (82’), находим решение поставленной задачи Коши.

Записываем ответ в виде .

Замечание 14. При решении уравнения Бернулли можно не приводить его к линейному, а искать решение в виде или применять метод вариации произвольной постоянной.