Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Характеристическое уравнение. Если в уравнении (34) коэффициенты постоянные, то оно называется линейным однородным уравнением с постоянными коэффициентами и имеет вид
(37),
где все 
вещественные числа, у – искомая функция, х – независимая переменная.
Решение этого уравнения ищется в виде 
. Это приводит к алгебраическому уравнению степени n 
(38), которое называется характеристическим.
Таким образом, чтобы составить характеристическое уравнение (39) надо в уравнении (37) заменить производные степенями неизвестной величины k, причем степень k должна быть равна порядку соответствующей производной, а сама искомая функция у заменена 1.
I. Если все корни характеристического уравнения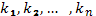 
числа вещественные и среди них нет равных между собой, то представляя значение корней в (*) получим n частных линейно независимых решений уравнения (37) в виде 
(**)
II. Если все корни характеристического уравнения числа вещественные, но среди них есть равные, то каждому корню 
кратности 
, соответствует линейно независимых частных решений уравнения (37) 
.
III. Если среди корней характеристического уравнения имеются комплексные, но не равные между собой, то каждой паре сопряженных комплексных корней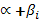 
и 
соответствует два частных линейно независимых решений уравнения (37) вида 
и 
(***)
Если же среди комплексных корней характеристического уравнения имеются кратные комплексные корни, то корню 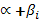кратности (корень имеет ту же кратность) соответствует частных линейно независимых решений уравнения (37), которые имеют вид
В заключение приведем схему решения линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами:
1) Составляем характеристическое уравнение
2) Находим корни характеристического уравнения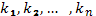
3) В зависимости от характера корней выписываем частные линейно независимые решения дифференциального уравнения
4) Подставляя их в формулу 
, получаем общее решение дифференциального уравнения (37)
Пример 15. Найти общее решение уравнения 
Составим характеристическое уравнение 
, его можно переписать в виде 
и найти его корни 
, им соответствуют решения 
Общее решение имеет вид: 
.
Линейные неоднородные дифференциальные уравнения
Предполагается, что функции 
и правая часть уравнения – функция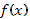 
непрерывны в промежутке (a, b), случаи 
не исключаются. Функции 
называются коэффициентами уравнения.
1. Линейное неоднородное дифференциальное уравнение имеет вид
(40)
2. Общее решение линейного неоднородного уравнения находится так:
а) Найти одно какое-нибудь его частное решение
б) Найти общее решение соответствующего однородного уравнения
в) Сложить эти два решения. Сумма их и будет общим решением уравнения (40)
Так, если частное решение неоднородного уравнения есть Y, а общее решение соответствующего однородного есть 
, то общее решение линейного неоднородного уравнения (40) 
(41)
3. Если правая часть уравнения (40) есть сумма двух функций
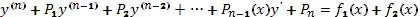(42)
Следует рассматривать два уравнения, у которых левые части такие же, как в (42), нов одном из них правой частью будет функция 
, а во втором 
, т.е. рассмотреть уравнение
(43)
(44)
Если функции 
и 
- соответственно частные решения уравнений (43) и (44), то их сумма 
будет частным решением (42) (это свойство называется положением решений и распространяется на случай, когда правая часть – сумма n решений)
4. Если известно общее решение однородного линейного уравнения, соответствующего заданному неоднородному, то его частное решение Y можно найти с помощью квадратур методом, который указал Лагранж. Этот метод называется методом вариации (изменения) произвольных постоянных.
Получив общее решение соответствующего однородного уравнения 
, поступают так: полагают, что в этом решении величины 
являются не постоянными, а функциями независимой переменной х. Записывают это так: 
Для определения функций 
составляется система уравнений:
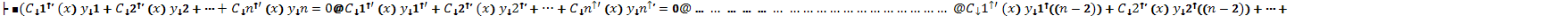(45)
Рассмотрим подробно этот метод для линейных дифференциальных неоднородных уравнений второго порядка 
(46)
Получив особое решение 
(47) соответствующего однородного уравнения поступают так: полагают, что в этом решении величины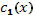 
и 
являются не постоянными, а функциями независимой переменной х и записывают 
Для определения функци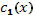й и составляется система (45)
(48)
Определитель этой системы – определитель Вронского; так как (47) есть общее решение (46), то функции 
и 
линейно независимы и их определитель не равен 0. Поэтому система (48) имеет всегда решение и притом единственное.
Решая эту систему уравнений относительно 
и 
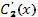, получим:
Где определитель Вронского 
Из (49) интегрированием находим 
Подставляя (50) в (47) получим
Раскрывая скобки, найдем 
Сравнивая с (41) замечаем, что первые два слагаемых 
в правой части – общее решение однородного уравнения, соответствующего (46), а последние два слагаемых – частное решение неоднородного уравнения (46)
Обозначая эти два слагаемых через Y, получаем формулу частного решения линейного неоднородного уравнения второго порядка 
В более компактной форме частное решение линейного неоднородного уравнения второго порядка может быть записано так:
Все величины, входящие в эту формулу известны.
Замечание 9. Следует иметь в виду, что система (48) так же, как и формула (51), имеет место тогда, когда коэффициент при старшей производной равен единице. Функция 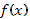есть правая часть уравнения при этом предположении.
Метод вариации произвольных постоянных – универсальный. Он позволяет при помощи квадратур определить частное решение линейного неоднородного дифференциального уравнения (34), если известно общее решение соответствующего ему однородного уравнения.
Пример 16. Проинтегрировать уравнение 
Корни характеристического уравнения 
комплексные сопряженные 
, следовательно, общее решение однородного уравнения есть 
Общее решение неоднородного уравнения ищем в виде 
, так как для данного примера 
, составляем систему
Из этой системы найдем функции и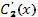
Подставив найденные значения 
и 
, получим общее решение данного дифференциального уравнения:
Дата добавления: 2018-02-15; просмотров: 641; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!