Метод неопределенных коэффициентов для определения частного решения неоднородного линейного уравнения с постоянными коэффициентами
Пусть в уравнении 
коэффициентами являются не функции, а вещественные числа, а его правая часть 
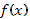имеет вид
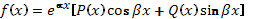(52), где 
и 
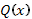- многочлены, которые могут быть одной и той же степени и разных степеней. Если они разной степени, то пусть n - их наивысшая степень (при 
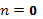эти многочлены попросту постоянные величины). Величины 
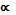и 
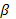- вещественные числа.
В рассматриваемом случае метод вариации произвольных постоянных для определения частного решения неоднородного уравнения, конечно, также применим. Однако, здесь можно отыскать частное решение более простым способом, пользуясь которым не понадобится вычислять интегралы. Интегрирование уравнения можно провести с помощью только алгебраических операций при помощи метода, который называется методом неопределенных коэффициентов.
Если правая часть имеет вид (52), то следует рассмотреть два случая.
1) Число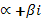 
не является корнем характеристического уравнения соответствующего однородного уравнения. В этом случае частное решение неоднородного уравнения ищется в виде 
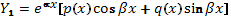(53), 
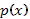и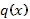 
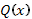- многочлены одной и той же степени, равной наивысшей степени многочленов и . Коэффициенты многочленов 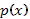и 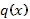- числа, подлежащие определению в (53), только эти коэффициенты и подлежат определению, числа же 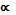и 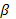те же, что и в (52).
2) Если число 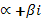является корнем кратности 
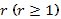характеристического уравнения, то частное решение неоднородного уравнения ищется в виде 
.
|
|
|
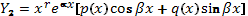Здесь многочлены 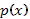и 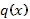, степень которых равна наивысшей степени многочленов и 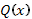подлежат определению; показатель степени 
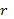равен кратности корня 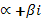характеристического уравнения. Таким образом, и в этом случае, определению подлежат только коэффициенты многочленов 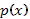и 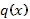, все же остальные числа 
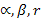- известны.
Неопределенные коэффициенты многочленов 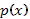и 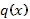как в том, так и в другом случае находятся так:
В заданное уравнение подставляется Y и сравниваются коэффициенты при одинаковых степенях независимой переменной в левой и правой частях уравнения.
Замечание 10. Рассматриваемый вид неоднородного линейного уравнения (коэффициенты постоянные, а правая часть имеет вид (52)) встречается очень часто, а механика их интегрирования исключительно проста.
Пример 17. Найти общее решение уравнения.
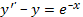
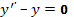
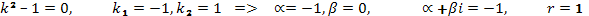
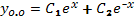
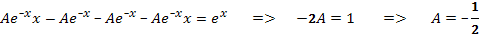
Уравнение Эйлера. Системы линейных дифференциальных уравнений с постоянными коэффициентами (основные понятия)
Уравнение Эйлера является линейным дифференциальным уравнением, которое имеет вид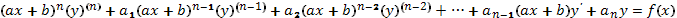 
(54), где все 
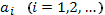, а также 
и 
- вещественные числа, а правая часть 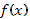- функция независимой переменной х, и по этой переменной вычислены все производные в (54).
|
|
|
В частном случае, когда 
уравнение (54) принимает вид
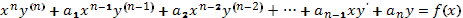(55)
Уравнение Эйлера (54) и (55) представляют собой частный случай линейных дифференциальных уравнений с переменными коэффициентами.
В приложениях математики уравнение Эйлера встречается часто. Если ввести замену независимой переменной по формуле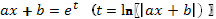 
(56) в случае, если уравнение имеет вид (54), или 
(57), если уравнение имеет вид (55), то уравнение Эйлера приводится к линейному уравнению с постоянными коэффициентами.
Из (56) следует
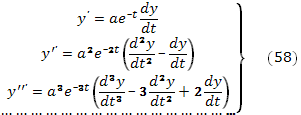
Делая в (54) замену переменных по формулам (44), это уравнение преобразуем в линейное дифференциальное уравнение с постоянными коэффициентами, которое мы умеем интегрировать.
Пример 18. а) Найти общее решение уравнения 
Решение: Это уравнение Эйлера типа (55). Произведем замену переменной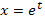 
по формуле (57) на основании (58) при 
и получим 
(58’)
Подставляя эти значения производных в заданное уравнение и замечая, что на основании (57)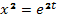 
, получаем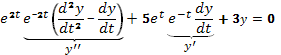 
Отсюда следует, что 
. Делая приведение подобных членов, имеем
Применяя формулы (58’), получим уравнение
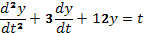(59)
которое является линейным неоднородным уравнением с постоянными коэффициентами. Поступаем так: отбрасываем правую часть и ищем общее решение уравнения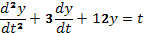
|
|
|
Его характеристическое уравнение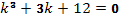 
имеет корни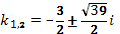 
Частные решения уравнения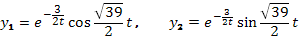 
, а его общее решение
.
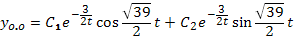Теперь отыщем частное решение уравнения (59). Сравнивая его с (52) 
, отмечаем, что 
. Число 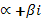не является корнем характеристического уравнения (среди его корней числа нуль нет). Частное решение ищем в виде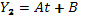 
Сравнивая коэффициенты при одинаковых степенях буквы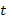 
в левой и правой частях, получим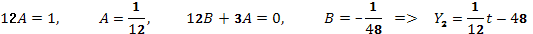 
. Теперь следует возвратиться к старой переменной х 
. Окончательно получим:
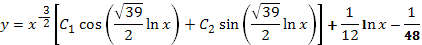
Сделанная подстановка привела нас к линейному уравнению с постоянными коэффициентами. Характеристическое уравнение имеет вид 
. Его корни: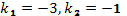 
.
Частные решения: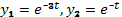 
. Теперь надо возвратиться к старой переменной 
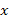. Из (57) следует, что 
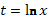. Частные решения запишутся в виде: 
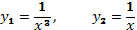, а общее решение заданного уравнения 
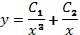, или окончательно 
Пример 18. б) Найти общее решение уравнения 
Предложенное уравнение – уравнение Эйлера. От уравнения, решенного ранее (см. а)), оно отличается наличием правой части, являющейся функцией той независимой переменной, по которой вычислены производные.
Как и раньше, это линейное уравнение с переменными коэффициентами может быть преобразовано к линейному уравнению с постоянными коэффициентами с помощью подстановки (57) 
|
|
|
Дата добавления: 2018-02-15; просмотров: 784; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!