Уравнения в полных дифференциалах
Постановка задачи. Найти интегральные кривые дифференциального уравнения
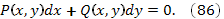
Алгоритм решения.
1. Если в некоторой области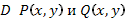 
имеют непрерывные частные производные и выполнено условие
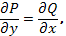
то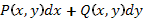 
- дифференциал некоторой функции 
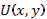. Тогда уравнение (86) называется уравнением в полных дифференциалах и может быть записано в виде
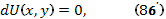
где 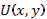- дважды непрерывно дифференцируемая неизвестная функция.
Из (86’) следует, что интегральные кривые определяются уравнением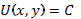 
при всех возможных С.
Для отыскания С заметим, что
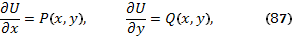
2. Интегрируя первое равенство в (87) по х, получим
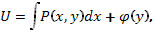
где - неизвестная функция, которую еще предстоит найти.
3. Дифференцируя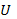 
по у, имеем
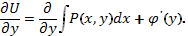
Используя второе равенство в (87), получим уравнение
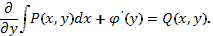
4. Находим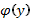 
и затем .
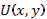Ответ. Интегральные кривые определяются уравнением 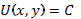при всевозможных значениях С.
Пример 26. Найти интегральные кривые дифференциального уравнения
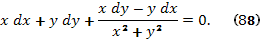
Решение.
1. Преобразуем уравнение (88):
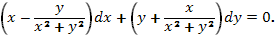
В данном случае
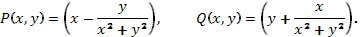
Эти функции непрерывно дифференцируемы в области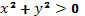 
.
Кроме того,
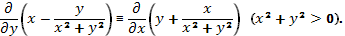
Поэтому 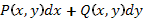- дифференциал некоторой функции 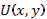в любой односвязной области 
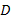, не содержащей точку 
. Следовательно, уравнение (88) является уравнением в полных дифференциалах и может быть записано в виде
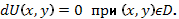
При этом
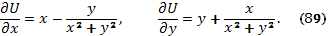
2. Интегрируя первое равенство в (89) по х, получим, что при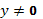 
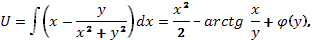
где 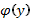- неизвестная функция, которую еще предстоит найти.
3. Дифференцируя 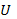по у, имеем
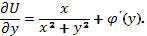
Используя второе равенство в (87), получим
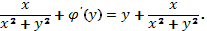
После преобразования имеем
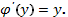
4. Отсюда
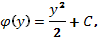
и, следовательно
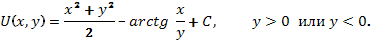
Ответ. Интегральные кривые в области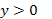 
или в области 
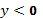определяются уравнением
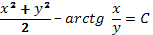
при всевозможных значениях С.
Условия задач. Найти интегральные кривые дифференциальных уравнений.
1. 
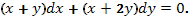Ответ: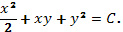 
2. Ответ: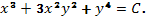 
12.21. Уравнения вида 
Постановка задачи. Найти общее решение дифференциального уравнения
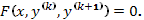
Алгоритм решения.
1. Полагая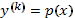 
, получим дифференциальной уравнение первого порядка
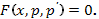
2. Определяя тип этого уравнения и применяя соответствующий метод решения, находим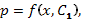 
где 
- произвольная постоянная.
3. Так как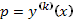 
, имеем
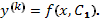
Последовательно интегрируя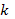 
раз (при каждом интегрировании не забывая о произвольной постоянной), получим ответ
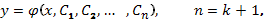
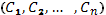– произвольный постоянные.
Пример 27. Найти общее решение дифференциального уравнения
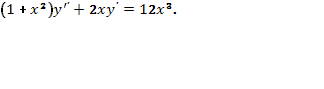
Решение.
1. поскольку дифференциальное уравнение не содержит у, то полагая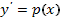 
, имеем 
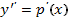. Получаем дифференциальное уравнение первого порядка
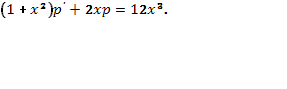
2. Уравнение
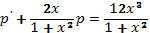
линейное относительно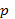 
и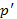 
. Решая его, например, методом вариации произвольной постоянной, находим
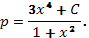
3. Так как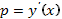 
, имеем
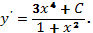
Интегрируя, получим общее решение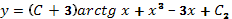 
.
Ответ.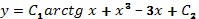 
.
Условия задач. Найти общие решения дифференциальных уравнений.
1. 
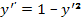. Ответ: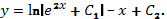 
2. 
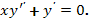Ответ: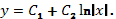 
12.22. Уравнения вида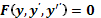 
Постановка задачи. Найти решение задачи Коши для дифференциального уравнения
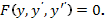
с начальными условиями
Алгоритм решения.
1. Поскольку дифференциальное уравнение не содержит явно независимой переменной х, полагаем
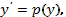
где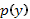 
- новая неизвестная функция. Тогда по формуле для произведения сложной функции имеем
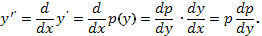
Получим уравнение первого порядка относительно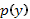
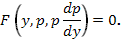
2. Определяя тип этого уравнения и применяя соответствующий метод решения, находим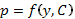 
, где С – произвольная постоянная.
3. Используя начальные условия (оба), находим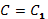 
.
4. Подставляя , получаем дифференциальное уравнение с разделяющимися переменными
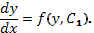
Разделяя переменные в области, где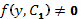 
, получаем
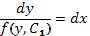
и, интегрируя, находим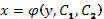 
.
Проверяем, не является ли решение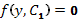 
особым решением исходного уравнения, удовлетворяющим начальным условиям.
5. Используем начальные условия для нахождения второй постоянной 
(значение уже найдено в п.3) и получаем решение задачи Коши.
Ответ записываем в виде 
или 
.
Пример 28. Найти решение задачи Коши для дифференциального уравнения
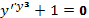
с начальными условиями 
.
Решение.
1. Поскольку дифференциальное уравнение не содержит явно независимой переменной х, полагаем
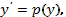
где 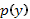– новая неизвестная функция. Тогда по формуле для производной сложной функции имеем
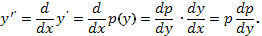
Получим уравнение первого порядка относительно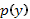
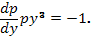
2. Разделяя переменные и интегрируя, находим
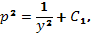
т.е.
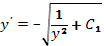
(знак минус мы выбрали из начального условия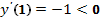 
).
3. Из начальных условий (обоих) имеем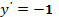 
при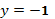 
. Отсюда, 
. Учитывая, что в силу первого начального условия 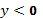и, следовательно, 
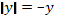, получаем
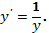
4. Разделяя переменные и интегрируя, находим
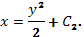
5. Из начального условия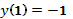 
получим 
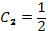. Следовательно,
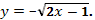
(Знак минус мы выбрали из начального условия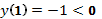 
.)
Ответ.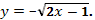
Условия задач. Найти решения задач Коши для дифференциальных уравнений
1. 
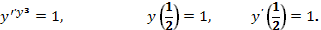Ответ:
2. 
Ответ: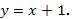 
Дата добавления: 2018-02-15; просмотров: 794; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!