Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами
а) Нормальной системой дифференциальных уравнений называется система уравнений вида:
В этой системе уравнений неизвестными являются n функций 
, а независимой переменной – 
.
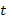Особенности нормальной системы дифференциальных уравнений:
1) Все входящие в систему уравнения являются уравнениями первого порядка
2) Все уравнения системы разрешены относительно производных искомых функций 
Если нормальная система уравнений (60) линейна, а коэффициенты при неизвестных функциях постоянны, то она имеет вид:
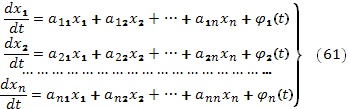
Все искомые функции входят в систему (61) в первой степени, а функции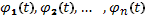 
- функции независимой переменной 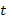, по которой вычислены производные.
Если все эти функции равны нулю, то система (61) называется однородной, а если хотя бы одна из них не равна нулю – неоднородной.
Число произвольных постоянных, входящих в общее решение нормальной системы уравнений, равно числу неизвестных функций, входящих в систему. Произвольные постоянные определяются из начальных или краевых условий.
Способ интегрирования нормальных систем линейных уравнений с постоянными коэффициентами покажем на примере однородной системы из трех уравнений.
Пример 19. Найти общее решение системы
(A)
Решение: Неизвестными функциями являются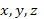 
, а независимой переменной – .
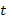Приведем решение этой системы к решению одного уравнения, порядок которого равен числу уравнений, входящих в систему.
|
|
|
Для этого любое из уравнений системы продифференцируем по 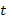и заменим в полученном уравнении производные 
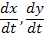и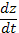 
их выражениями из системы.
Поступая так, например, с первым уравнением, получим 
.
Заменим в этом уравнении производные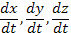 
, стоящие в правой части, их выражениями из второго и третьего уравнений заданной системы и получим уравнение
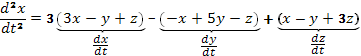, откуда после приведения подобных членов в правой части найдем 
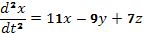(B)
Это уравнение опять дифференцируем по 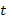и получим 
Снова заменим в правой части производные 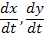и 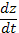их выражениями из заданной системы и получим уравнение 
, которое после приведения подобных членов в правой части запишется так: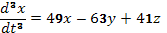 
(С).
Рассмотрим систему уравнений, состоящую из первого уравнения заданной системы, т.е. уравнения, обе части которого мы дифференцировали, и уравнений (B) и (С)
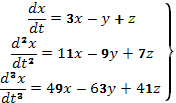(D)
Чтобы прийти к уравнению, содержащему только одну неизвестную функцию, из первых двух уравнений системы (D) определим функции 
и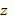 
. Из этих уравнений следует:
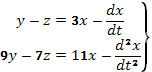
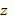Решая их относительно и , получим 
(E)
Подставляя эти значения и 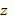в третье уравнение системы (D), найдем
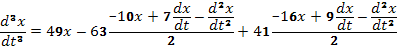
После упрощений в правой части получаем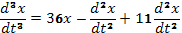 
(F)
Уравнение (F) – линейное однородное уравнение третьего порядка с постоянными коэффициентами. Перепишем его так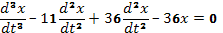 
(G) и найдем его общее решение по известным правилам.
|
|
|
Составляем характеристическое уравнение: 
.
Корнями этого уравнения являются 
Частными решениями уравнения (G) будут функции: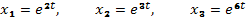 
, а его общим решением 
.
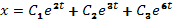Чтобы определить две остальные неизвестные функции и 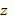, воспользуемся выражением (Е). После подстановки в (Е) выражени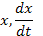й 
и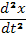 
получим:
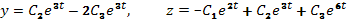
Дата добавления: 2018-02-15; просмотров: 1039; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!