Эффектом Доплера называют изменение частоты колебаний, воспринимаемых приемником при движении приемника и источника относительно друг друга. 6 страница

4. Определите силу тяжести. Как значение силы тяжести влияет на значение сил реакции и силы трения скольжения?

5. Сформулируйте определение веса тела. При каких условиях может наступить состояние невесомости?

6. Дайте определение массы, как меры инерции тела, и массы, как меры гравитационного взаимодействия.

7. Как связаны между собой законы Гука для различных видов деформаций?

8. При каких условиях возникает сила трения качения? Приведите примеры.

9. Обоснуйте исторический переход от скользящих механизмов к катящимся.

10. В чем заключается принцип относительности Г. Галилея?

11. Сформулируйте закон всемирного тяготения? Как определяется ускорение свободного падения на поверхности любой планеты?

12. Пользуясь таблицей 3.1 – «Некоторые данные о планетах Солнечной системы», определите ускорение свободного падения на Земле, Луне и любой планете Солнечной системы.

13. Пользуясь таблицей 3.1 – «Некоторые данные о планетах Солнечной системы», составьте и решите задачу на расчет силы всемирного тяготения.

Таблица 3.1 – Некоторые данные о планетах Солнечной системы

Планета	Среднее расстояние от Солнца (млн. км)	Период обращения вокруг Солнца (зем. год)	Экваториальный диаметр (км)	Масса (кг)
Земля	150	1	12742	5,96∙10²⁴
Луна	--	--	1740	7,3∙10²²
Меркурий	57,9	0,24	4840	3,22∙10²³
Венера	108	0,62	12400	4,83∙10²⁴
Марс	227,8	1,88	6780	6,38∙10²³
Юпитер	777,8	11,86	139760	1,90∙10²⁷
Сатурн	1426,1	29,46	115100	5,67∙10²⁶
Уран	2869,1	84,02	51000	8,69∙10²⁵
Нептун	4495,6	164,8	50000	1,03∙10²⁶
Плутон	5229	249,7	--	--

10.

Две гири массами 2 кг и 1 кг соединены нитью и перекинуты через невесомый неподвижный блок. Найти вес грузов во время движения. Трением нити о блок и весом нити пренебречь.

11. К одному концу верёвки, перекинутой через блок, подвешен груз массой 10 кг. С какой силой F нужно тянуть вниз за другой конец веревки, чтобы груз поднимался с ускорением 1 м/с²? Растяжением верёвки, её весом и трением о блок пренебречь (рис. 3.22).

12. Неподвижный блок подвешен к динамометру (рис. 3.23). Через блок перекинут невесомый шнур, на концах которого укреплены грузы с массами 2 кг и 8 кг. Что показывает динамометр при движении грузов? Весом блока и трением шнура пренебречь.

13. Задача про элементарный полиспаст. Найти натяжение нити Т в устройстве, изображенном на рисунке 3.24 к задаче. Массы тел равны 100 г и 300 г. Весом блоков и трением нити о них пренебречь. Определить ускорения тел.

Рекомендованная литература

1. Волькенштейн В.С. Сборник задач по общему курсу. – М.: Главная ред. физ.-мат. литературы, 1987. – 456 с. – (Задачи №№ 2.1-2.35).

2. Евграфова Н.Н., Каган В.Л. Курс физики. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1978. – 512 с. – С. 57-67.

3. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М.: Просвещение, 1982. – 448 с. – С. 68-83.

4. Трофимова Т.И. Курс физики. – М.: ВШ, 1990. – 478 с. – С. 14-18.

ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. РЕАКТИВНОЕ ДВИЖЕНИЕ.

ЗАКОН ДВИЖЕНИЯ ЦЕНТРА МАСС

План

1 Механические системы.

2 Импульс.

3 Закон сохранения импульса.

4 Однородность пространства.

5 Центр масс.

6 Закон движения центра масс.

7 Уравнение движения тела переменной массы.

8 Формула Циолковского.

9 Примеры решения задач.

1 Механические системы

Механическими системами называют совокупность материальных точек тел, рассматриваемых как единое целое.

Механическими системами являются:

s материальная точка;

s математический маятник;

s абсолютно твердое тело;

s деформируемое тело;

S сплошная среда.

Тела (материальные точки) механической системы движутся согласно законам классической механики; взаимодействуют друг с другом и с телами, не включенными в эту совокупность.

Силы взаимодействия материальных точек механической системы между собой называют внутренними.

Внешними называют силы, с которыми на материальные точки механической системы действуют тела, в нее не входящие.

Механическая система является замкнутой (изолированной), если на нее не действуют внешние силы или действие внешних сил скомпенсировано. Для замкнутой системы по I закону Ньютона геометрическая сумма внутренних сил равна нулю.

2 Импульс

Понятие «количество движения» было введено И. Ньютоном в «Математических началах натуральной философии» (1687). Впоследствии это понятие было учеными заменено понятием «импульс». А в современной физике «количество движения» практически не используется.

Импульс – физическая величина, численно равная произведению массы тела на его скорость:

В СИ: .

3 Закон сохранения импульса

Рассмотрим механическую систему, состоящую из n тел, массы которых , а скорости – . Пусть 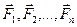– равнодействующие внутренних сил, действующие на тела системы, – равнодействующие внешних сил, действующих на каждое тело.

Запишем II закон Ньютона для каждого тела:

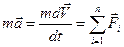a a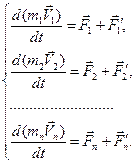

Просуммируем уравнения между собой:

;

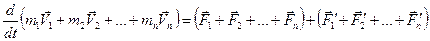Т.к. по ІІІ закону Ньютона , то:

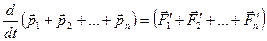Окончательно получаем II закон Ньютона для механической системы:

–

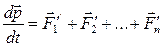первая производная от суммарного импульса замкнутой системы тел по времени равна геометрической сумме всех внешних сил, действующих на тела этой системы.

Для замкнутой механической системы сумма внешних сил, действующих на тела этой системы, равна нулю: 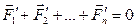. В этом случае 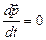, т.е.:

–

импульс замкнутой системы тел сохраняется, т.е. не изменяется со временем, при любых взаимодействиях между телами системы. Таким образом, из II закона Ньютона получен закон сохранения импульса.

При решении задач удобнее записывать закон сохранения импульса в форме:

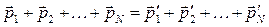в замкнутой механической системе геометрическая сумма импульсов тел до взаимодействия равна геометрической сумме импульсов тел после взаимодействия.

4 Однородность пространства

Однородность пространства заключается в том, что физические свойства механической системы и законы движения не зависят от выбора начала координат инерциальной системы отсчета.

Закон сохранения импульса является следствием однородности пространства.

5 Центр масс

Центр масс в механике – это геометрическая точка, характеризующая движение тела или системы частиц как целого.

Центр масс системы тел называется точка С, положение которой характеризует распределение масс в этой системе.

Радиус-вектор центра масс определяется выражением:

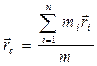Понятие центра масс широко используется в физике.

Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

Легко видеть, что в однородном поле тяготения центр масс совпадает с центром тяжести. Поэтому положение центра масс тела сложной формы можно практически определить путем последовательного подвешивания его за несколько точек и отмечая по отвесу вертикальные линии (рис. 4.2).

Равнодействующая сил тяжести в однородном поле тяготения приложена к центру масс тела. Если тело подвешено за центр масс, то оно находится в состоянии безразличного равновесия. Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности (рис. 4.2). При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка.

6 Закон движения центра масс

Скорость центра масс равна первой производной радиус-вектора центра масс по времени:

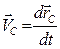Массу тела можно рассматривать как сумму элементарных масс системы:

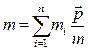Радиус-вектор центра масс определяется выражением:

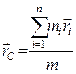Тогда скорость центра масс будет равна:

Следовательно,

–

импульс системы равен произведению массы механической системы на скорость центра масс.

Если полученное значение импульса системы подставить во II закон Ньютона для механической системы в дифференциальной форме, то получим:

–

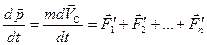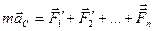закон движения центра масс: центр масс системы материальных точек движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.

Вывод: для замкнутых систем действие внешних сил равно нулю или скомпенсировано:

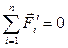, т.е. .

Следовательно, – т.е. центр масс замкнутых систем движется равномерно.

Центр масс замкнутой системы относительно произвольной инерциальной системы отсчета движется равномерно прямолинейно или покоится. Изменение импульса центра масс происходит за счет внешних сил.

Внутренние силы не влияют на характер движения замкнутой системы тел, если внешнее воздействие на систему постоянно и однородно. Например, во время салюта движение центра масс разорвавшегося пиротехнического снаряда в постоянном однородном поле силы тяжести происходит по параболе.

Если внешнее воздействие изменяется, то на различные части системы начинают действовать разные силы и характер движения центра масс меняется. В качестве примера рассмотрим движение системы, состоящей из одного тела – снаряда. В случае падения одной из частей разорвавшегося в воздухе снаряда на землю в системе появится новая внешняя сила – сила реакции опоры. Характер движения центра масс системы (осколков снаряда) при этом изменится. Наличие внутренних сил в этом примере является необходимым условием изменения характера движения центра масс системы. Без этих сил, обусловивших распад снаряда на части, не произошло бы изменения траектории его движения вплоть до падения снаряда на землю.

7 Уравнение движения тела переменной массы

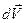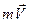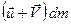Пусть в момент времени t масса ракеты m, а скорость . Через время dt масса ракеты изменилась на dm, а скорость ракеты на . Тогда: – начальный импульс ракеты; – конечный импульс; – импульс вытекающих газов.

Найдем изменение импульса ракеты за время dt:

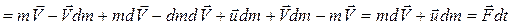Если полученное выражение разделить на dt, то получим:

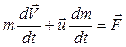Если 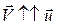, то ракета тормозится; если 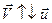, то ракета движется с ускорением. Следовательно, 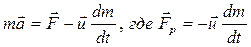– реактивная сила, которая создается вытекающими газами массы dm со скоростью .

Полученное уравнение:

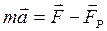
носит название уравнения Мещерского – основное уравнение в механике тел переменной массы, полученное в 1904 году Иваном Всеволодовичем Мещерским (1859-1935), русским учёным, основоположником механики тел переменной массы. В выдающемся труде «Уравнения движения точки переменной массы в общем случае» (1904) его теория получила окончательное и в высшей степени изящное выражение. Здесь он устанавливает и исследует общее уравнение движения точки, масса которой изменяется от одновременного процесса присоединения и отделения материальных частиц.

И.В. Мещерский рассмотрел большое количество частных задач о движении точки переменной массы, например восходящее движение ракеты и вертикальное движение аэростата. Он подверг весьма обстоятельному исследованию движение точки переменной массы под действием центральной силы, заложив тем самым основания небесной механики тел переменной массы. Он исследовал также и некоторые проблемы движения комет.

И.В. Мещерский впервые сформулировал и так называемые обратные задачи, когда по заданным внешним силам и траекториям определяется закон изменения массы. Кроме работ по механике переменных масс, ему принадлежит ряд работ по общей механике.

С началом полётов в космос с достаточной полнотой выяснилось огромное практическое значение исследований И.В. Мещерского по механике переменных масс. Опираясь на его труды, учёные разработали основные вопросы динамики твёрдого тела произвольных изменяемых систем переменной массы.

Исследования И.В. Мещерского явились теоретической основой современной ракетодинамики. Его имя неразрывно связано с именем одного из создателей научных основ космонавтики – К.Э. Циолковского.

8 Формула Циолковского

Если система «ракета-газы» замкнута, то действие внешних сил отсутствует, т.е. . Тогда уравнение Мещерского преобразуется в дифференциальное уравнение первого порядка с разделяющимися переменными:

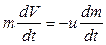при , .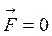

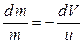После интегрирования получим: .

В начальный момент времени, когда 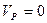, , 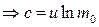. Тогда получаем:

–

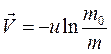формулу Циолковского, где определяется скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.

Дата добавления: 2021-05-18; просмотров: 68; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!