Задания для самостоятельной работы.

Стр 1 из 13Следующая ⇒

Федеральное государственное образовательное учреждение

высшего образования

«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»

Департамент анализа данных, принятия решений и

Финансовых технологий

В.В. УГРОЗОВ, А.А.БЕЛЯЕВ, А.В. ТРЕГУБ

ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ

Практикум

Для самостоятельной работы студентов

Для студентов, обучающихся

по направлению подготовки 38.03.02 «Менеджмент»

профили «Инвестиционный менеджмент, Финансовый менеджмент »

(программа подготовки бакалавров)

Москва – 2017

Федеральное государственное образовательное учреждение

высшего образования

«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»

Департамент анализа данных, принятия решений и

Финансовых технологий

В.В. УГРОЗОВ, А.А.БЕЛЯЕВ, А.В. ТРЕГУБ

ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ

Практикум

Для самостоятельной работы студентов

Для студентов, обучающихся

по направлению подготовки 38.03.02 «Менеджмент»

профиль «Инвестиционный менеджмент, Финансовый менеджмент»

(программа подготовки бакалавров)

Одобрено на заседании Совета департамента

анализа данных, принятия решений и финансовых технологий

(протокол № от 2017 г.)

Москва – 2017

УДК 336:51(076.5)

ББК 65.26в631

У 27

Рецензент: И.В,Орлова, к.э.н.,профессор Департамента анализа данных, принятия решений и финансовых технологий.

Угрозов В.В., Беляев А.А., Трегуб А.В. «Основы финансовых вычислений» / Практикум для самостоятельной работы студентов. М.: Финансовый университет при Правительстве РФ, департамент анализа данных, принятия решений и финансовых технологий, 2017. 122 с.

Практикум предназначен для бакалавров очной и заочной формы обучения по направлению подготовки: 38.03.02 «Менеджмент», профили «Инвестиционный менеджмент, Финансовый менеджмент».

УДК 336:51(076.5)

ББК 65.26в631

Учебное издание

Угрозов Валерий Вячеславович, Беляев Александр Афанасьевич, Трегуб Андрей Владимирович

«Основы финансовых вычислений »

Практикум для самостоятельной работы студентов

Компьютерный набор В.В.Угрозов, А.А.Беляев, А.В.Трегуб,

Компьютерная верстка В.В.Угрозов, А.А.Беляев, А.В.Трегуб

Формат 60х90/16. Гарнитура Т imes New Roman

Усл. п.л. 7,5

© В.В.Угрозов, А.А.Беляев, А.В.Трегуб 2017

© Финуниверситет, 2017

Тема 1. Процентные вычисления

В финансовых вычислениях под процентом понимается величина дохода, выплачиваемая заемщиком кредитору за использование им заёмных денежных средств. Деньги могут быть помещены на банковский сберегательный счет, использованы при покупке депозитного сертификата, выдаче ссуды, продаже в кредит, покупке облигаций, акций и т.п. В операциях наращения и дисконтирования используется коэффициент, который называется процентной ставкой. Ставкой процента, или просто процентом, называют отношение, выраженное в процентах, дохода за фиксированный промежуток времени (период начисления) на денежные средства, предоставленные в долг, к размеру этих денежных средств.

1.1. Начисление простого процента

При использовании простого процента, процент начисляется на первоначально вложенную сумму PV (present value). При этом сумма процента, начисленного в предыдущие периоды, не принимается в расчёт в процессе последующего наращения. Наращенная сумма FV (future value) при ежегодном начислении процентов равна

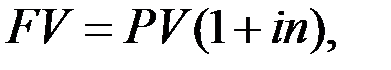(1.1)

где i – годовая процентная ставка, п - число лет.

Из формулы (1.1) легко можно найти количество лет, необходимое для увеличения начальной суммы в N раз

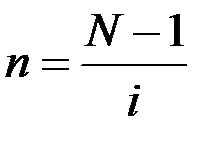. (1.2)

Если проценты начисляются в течение времени T (дней), то для простых процентов наращенная сумма рассчитывается по формуле

(1.3)

где 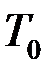– число дней в финансовом году.

На практике обычно используют три варианта начисления процентов:

1) точные проценты с точным числом дней вклада (ссуды) (АСТ/АСТ).

В этом случае 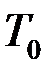= 365/366, а продолжительность месяца равна календарной;

2) обыкновенные проценты с точным числом дней вклада (ссуды) (АСТ/360). Здесь 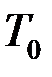= 360, а месяц равен календарному числу дней;

3) обыкновенные проценты с приближённым числом дней вклада (ссуды) (360/360).

При таком варианте расчёта 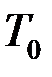= 360, а продолжительность месяца равна 30 дням.

Если на разных промежутках начисления процентов 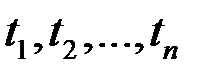устанавливаются разные годовые ставки процентов 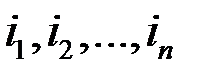, то наращенная сумма FV за время равна

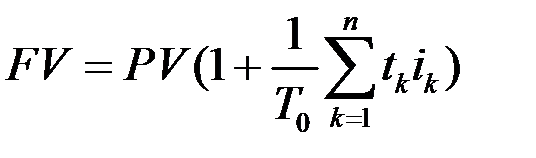. (1.4)

Пример 1. Ссуда 700000 руб. выдана на квартал по простой ставке процентов 15% годовых. Определить наращённую сумму.

Решение. Наращенную сумму найдем по формуле (1.3)

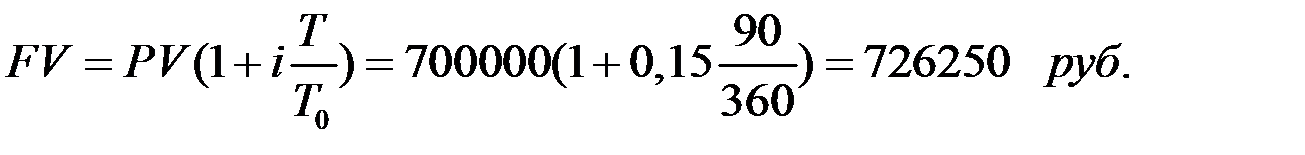
Таким образом долг вырос на 26250 рублей.

Пример 2. Вклад в размере 100000 рублей открыт в банке 16 апреля под 10 % годовых по схеме простых процентов. Какую сумму получит вкладчик 1 сентября? (АСТ/АСТ)

Решение. Размер вклада на момент закрытия вклада найдем по формуле (1.3) с учетом правила АСТ/АСТ

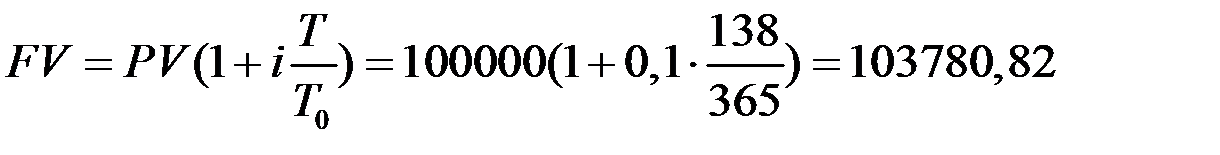рублей.

Пример 3. В банкеоткрыт депозит в размере 100000 рублей, на которые начисляются простые проценты. Найти размер вклада через 5 лет, если в первые два года процентная ставка составляла 12% годовых, а в оставшиеся три года её величина была равна 10%.

Решение. Размер вклада через 5 лет найдем по формуле (1.4)

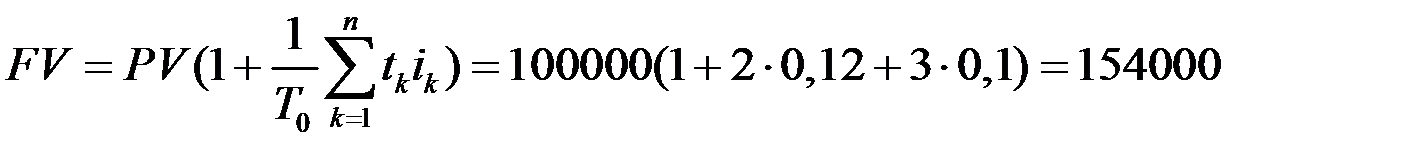рублей.

Начисление сложного процента

При использовании сложного процента, процент начисляется на наращенную в предыдущие моменты времени сумму. Поэтому этот процент называют ещё и процессом капитализации.

Величина наращенной суммы при ежегодном начислении сложных процентов равна

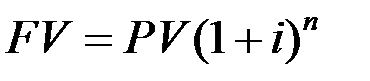. (1.5)

где i - годовая процентная ставка, n - число лет.

Если проценты начисляются в течение времени T, то для сложных процентов наращенная сумма рассчитывается по формуле

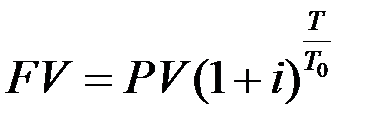. (1.6)

При дробном числе лет, наряду с формулой (1.6), часто используется формула смешанного процента

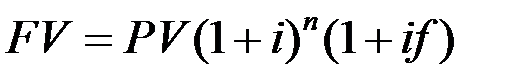, (1.7)

где n - целая часть числа 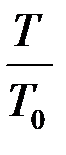, а f - дробная его часть.

Пример 4. Найти величину вклада, размещенного в банке на срок 180 дней (АСТ/360) под 10% годовых, если начальная величина вклада равна 1 млн. рублей?

Расчеты проведите по формуле простых и сложных процентов.

Решение. Величину вклада через T= 180 дней найдём по формулам (1.3) и (1.6) соответственно.

- в схеме простых процентов 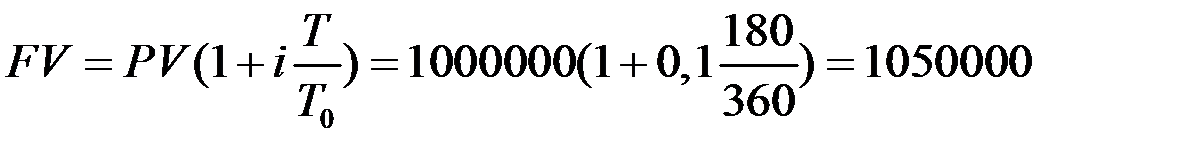(руб.)

- в схеме сложных процентов рублей.

Полученная величина оказалась почти на 1200 рублей меньше соответствующей величины, вычисленной по формуле простого процента.

Пример 5. Найти величину вклада, размещенного в банке на срок 2 года под 10% годовых, если начальная величина вклада равна 1 млн. рублей? Расчеты проведите по формуле простых и сложных процентов.

Решение. Величину вклада через n= 2 года найдём по формулам (1.1) и (1.5) соответственно.

- в схеме простых процентов 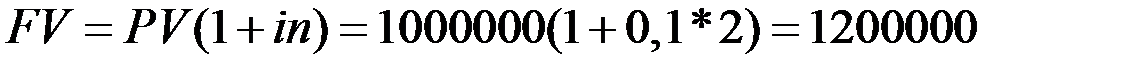(руб.)

- в схеме сложных процентов 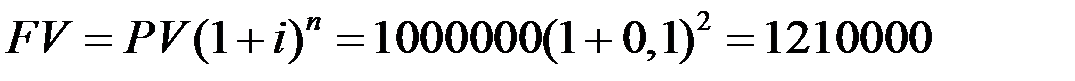(руб.)

Полученная величина на 10000 рублей больше соответствующей величины, вычисленной по формуле простого процента.

Пример 6. Найти величину вклада, размещенного в банке на срок 2,5 года под 10% годовых, если начальная величина вклада равна 1 млн. рублей. Расчеты проведите по формуле смешанного процента.

Решение. Искомуювеличину вклада найдём по формуле (1.7)

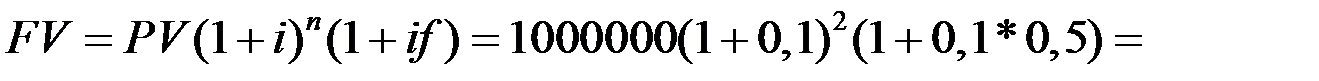1270500 рублей.

Если начисление сложных процентов происходит несколько раз в году (кратное начисление процентов), то расчёт наращенной суммы производят по формуле

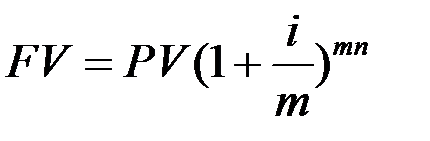, (1.8)

где m – кратность начислений, п – количество лет, i – годовая процентная ставка.

Из последней формулы видно, что наращенная сумма зависит от частоты начисления процентов. Чем больше частота начисления процентов, тем больше наращенная сумма.

Пример 7. Банк открывает депозиты по ставке 10% годовых, предлагая различные схемы начисления сложного процента. Найдите величину вклада через два года при начислении сложного процента: а) 1; б) 4; в) 6; г) 12 раз в году, если начальная сумма вклада равна 1 млн. руб. Ответы округлите до рублей.

Решение. Величину вклада найдем по формуле (1.8)

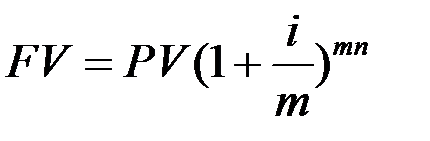
а) рублей.

б) 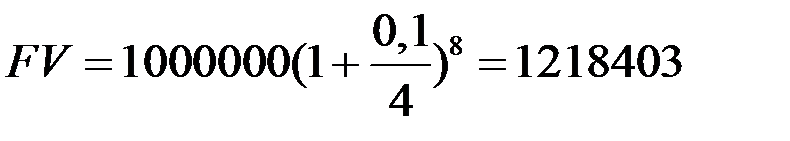рублей.

в) рублей.

г) 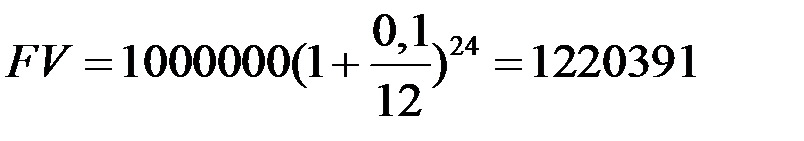рубль.

Из формулы (1.8) можно найти количество лет, необходимое для увеличения начальной суммы в N раз. Для случая, когда проценты начисляются один раз в год, это число равно

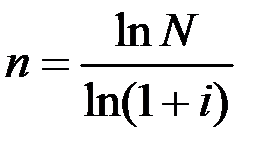. (1.9)

В случае, когда проценты начисляются m раз в году, искомое число лет будет равным

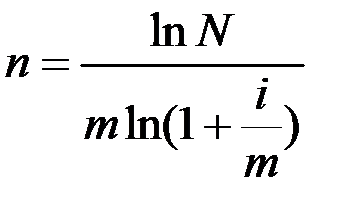. (1.10)

Пример 8. Найти величину вклада, размещенного в банке на 5 лет, если начальная величина вклада равна 1 млн. рублей. В первые два года банк начислял 12% годовых ежеквартально, а в оставшиеся три года – 10% годовых ежемесячно.

Решение. Величину вклада через пять лет найдем, используя формулу (1.8)

руб.

Пример 9. За сколько лет произойдёт удвоение капитала при начислении сложных процентов раз в год по процентной ставке 10%?

Решение. Количество лет, необходимое для увеличения начальной суммы в 2 раза найдём по формуле (1.9)

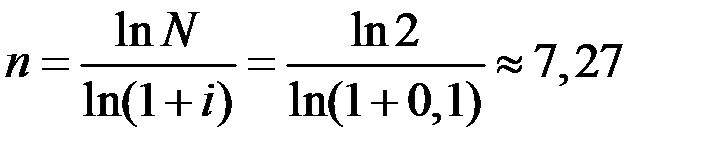лет.

Для небольших процентных ставок ( 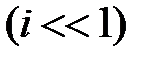) можно использовать приближённую формулу — «правило 70», согласно которому удвоение капитала происходит за 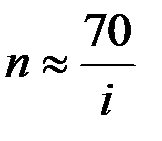лет. Например, при ставке 10% удвоение капитала произойдёт примерно за 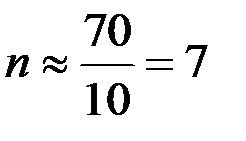лет.

Если частота начислений 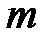стремится к бесконечности 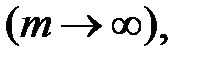то говорят о непрерывном начислении сложных процентов. В этом случае наращенная сумма за n лет находится по формуле

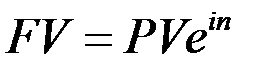. (1.11)

Если проценты начисляются в течение времени T, то наращенная сумма рассчитывается по формуле

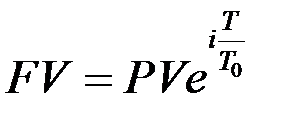. (1.12)

Если на разных промежутках начисления процентов 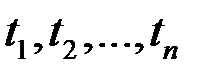устанавливаются разные годовые ставки процентов 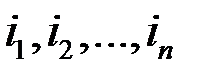, то наращенная сумма FV за время вычисляется по формуле

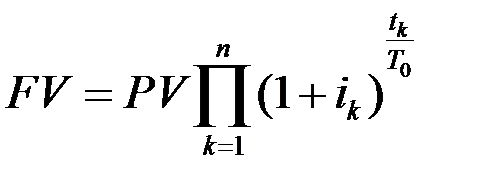. (1.13)

1.3. Эффективные и номинальные процентные ставки

Эффективной процентной ставкой 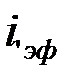называется годовая ставка сложных процентов, дающая тот же финансовый результат, что и при любой другой схеме выплат:

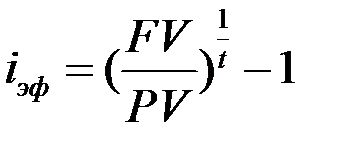. (1.14)

Под номинальной (объявленной) процентной ставкой 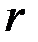понимается годовая ставка, которую назначает банк для начисления процентов.

Если проценты начисляются т раз в год по схеме сложных процентов, то эффективная процентная ставка в этом случае равна

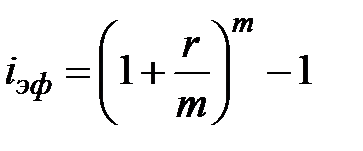. (1.15)

В случае непрерывного начисления сложных процентов эффективная процентная ставка определяется следующим выражением:

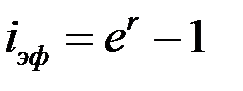(1.16)

Эффективная процентная ставка позволяет сравнивать доходности при различных схемах начисления процентов.

Пример 10. Найдите эффективную годовую процентную ставку, если банк начисляет проценты раз в квартал, а номинальная годовая процентная ставка составляет 12 %.

Решение. Эффективную годовую процентную ставку находим по формуле (1.15).

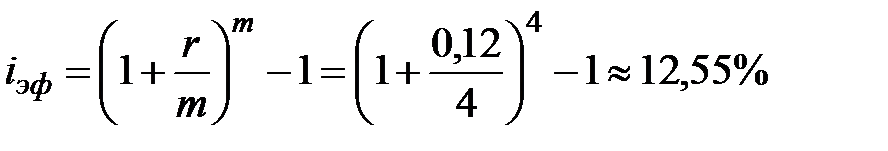
Ставки называют эквивалентными, если при одинаковой начальной сумме, накопленные к любому моменту времени t суммы, наращенные по различным схемам начисления процентов, совпадают.

Если j – годовая ставка при кратности начисления m , то ей эквивалентна ставка 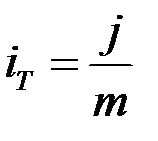за период 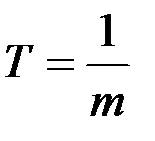. Эквивалентная эффективная ставка определяется из выражения

(1.17)

или 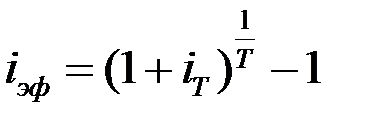(1.18)

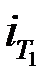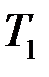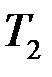Ставки и с периодами начисления и соответственно эквивалентны, если

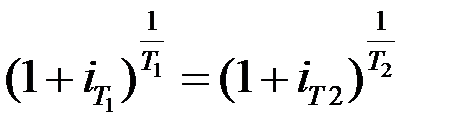(1.19)

Пример 11. Найти месячную процентную ставку, эквивалентную 12% номинальной годовой ставке при ежемесячном начислении процентов.

Решение. Эквивалентную ставку найдем из соотношения

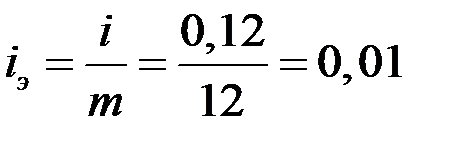Таким образом, за один месяц процентная ставка составила 1 %.

Пример 12. На вклад начисляется с капитализацией ежемесячно 1%. Найти эквивалентную ставку при ежеквартальном начислении процентов.

Решение. Эквивалентную ставку найдем из соотношения (1.19)

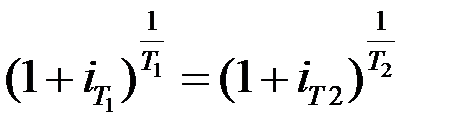Подставляя в выражение заданные значения, получим

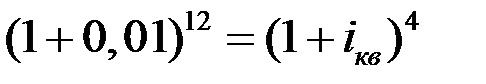Откуда находим величину процентной ставки.

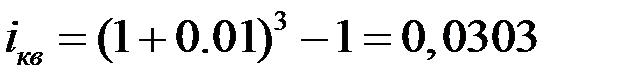или 3,03%

1.4. Дисконтирование. Банковский учёт

Различают понятия математического дисконтирования, и банковского учёта. В некотором смысле они являются обратными по отношению к начислению процентов. Математическое дисконтирование решает задачу о нахождении начальной суммы PV, если известна наращенная за п лет сумма FV и ежегодная процентная ставка i. В случае начисления простых процентов из формулы (1.1) будем иметь

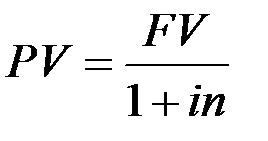. (1.20)

При начислении сложных процентов т раз в году начальная сумма PV равна

(1.21)

Если проценты начисляются непрерывно, то из (1.11) имеем

(1.22)

При этом величина i называется ставкой дисконтирования.

Пример13. Какую сумму нужно положить на счет в банк под 10% годовых (сложные проценты), чтобы через два года на счете было 1210000 рублей.

Решение. Для нахождения искомой величины вклада, воспользуемся формулой (1.21)

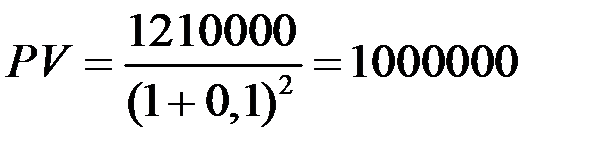рублей.

По времени начисления процентов различают антисипативный (предварительный) метод – начисление процентов происходит в начале расчётного периода, и декурсивный (последующий) метод – начисление процентов происходит в конце расчётного периода. При антисипативном методе начисления сумма процентных денег определяется, исходя из наращенной суммы. При декурсивном методе – величина начисляемых процентов определяется из величины предоставляемого капитала.

Банковский учёт (учет векселей) заключается в покупке банком денежных обязательств по цене меньшей номинальной, указанной в них суммы. Примером денежных обязательств может служить вексель – долговая расписка, которая содержит обязательство выплатить определённую денежную сумму (номинал) в конкретное время. В этом случае говорят, что вексель учитывается. При этом клиенту выплачивается сумма после удержания

PV = FV — D, (1.23)

где FV - номинальная сумма векселя, PV - цена покупки векселя банком за п лет до погашения, D - дисконт - доход банка.

Если вексель учитывается за один год до погашения, то величина дисконта равна

D = FVd, (1.24)

где d - учётная ставка.

Сумма, которую получит векселедержатель за п лет до погашения векселя в случае простой учётной ставки, составит

PV = FV( 1 — nd). (1.25)

В случае сложной учётной ставки

PV = FV (1 — d)ⁿ . (1.26)

Число лет п (время, оставшееся до погашения векселя) может быть любым положительным числом. Если срок учёта менее одного года, то более выгодным для банка является дисконтирование по сложной учётной ставке. Если же срок учёта превышает один год, то более выгодным является дисконтирование по простой учётной ставке.

Пример14. Вексель стоимостью 1 млн. руб. учитывается за три года до погашения по а) простой; б) сложной учётной ставке 10% годовых. Найдите сумму, которую получит векселедержатель, и величину дисконта.

Решение. Векселедержатель получит сумму

а) PV = 1000000(1 - 0.10*3) = 700000 руб.

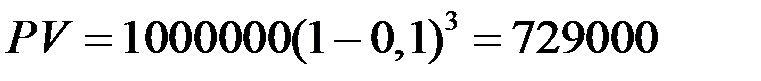б) руб.

Величина дисконта равна

а) D = 1000000 — 700000 = 300000 руб.

б) D = 1000000 — 729000 = 271000 руб.

1.5. Конверсия платежей

Эквивалентными платежами называют такие платежи, для которых сумма заменяемых платежей, приведенных к базисной дате, равна сумме платежей по новому обязательству, приведенных к той же дате.

Примером эквивалентных платежей является консолидация платежей, когда несколько платежей 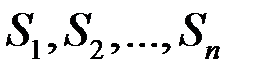со сроками оплаты соответственно заменяют одним платежом 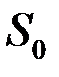и сроком оплаты 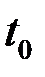. При решении задач на консолидацию платежей находят либо величину консолидированного платежа, либо время его выплаты. При заданном времени платежа 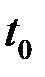, если консолидация производится по ставке простых процентов 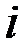, размер консолидированного платежа равен

. (1.27)

Здесь предполагается, что первые m платежей выплачиваются при 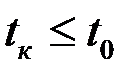, а оставшиеся платежи со сроками оплаты .

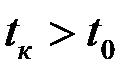Если консолидация производится по ставке сложных процентов 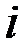, то размер консолидированного платежа составит

(1.28)

Время оплаты 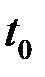консолидированного платежа 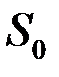для ставки простых процентов 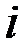можно найти из соотношения

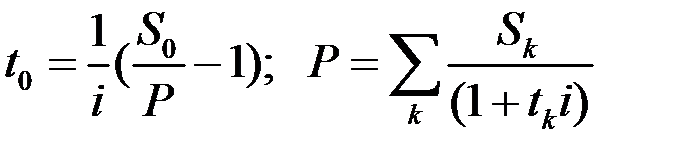(1.29)

Формула (1.29) имеет смысл при размере консолидированного платежа .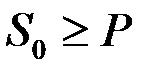

Для ставки сложных процентов 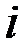время оплаты 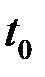консолидированного платежа 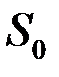равно

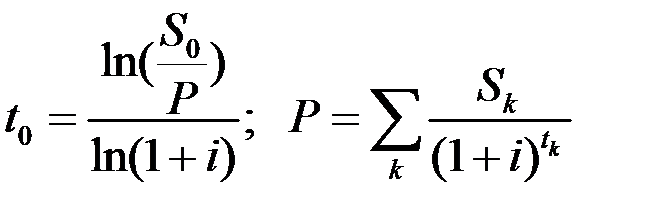. (1.30)

Пример 15. Платежи 1,15 млн. руб.; 1,35млн. руб. и 1,6 млн. руб. со сроками уплаты соответственно через 1,5; 2 и 2,5 года объединяются в один через 3,5 года. Консолидация проводится по сложной ставке 11% годовых. Определить консолидированный платеж.

Решение. Величину консолидированного платежа найдем как сумму (в млн. руб.) наращенных к указанному сроку (t =3,5) отдельных платежей:

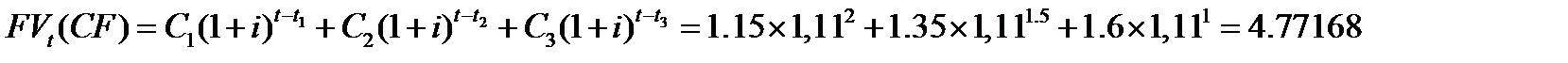
Пример 16. Суммы в размере 11,5 млн. руб.; 12,5 млн. руб. и 11 млн. руб. должны быть выплачены через 35; 75 и 80 дней соответственно. Стороны согласились заменить их одним платежом 36 млн. руб. по ставке 10% простых годовых при К=365. Определить срок консолидированного платежа.

Решение. Для определения величины консолидированного платежа определяем наращенную стоимость каждого из платежей. Для этого используем формулу простых процентов (1.1):

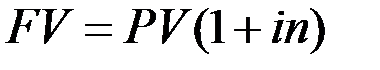
Поскольку в данном случае условие оперирует сроками, выраженными в днях (d), формула приобретает следующий вид:

Записываем выражения для определения наращенной суммы по каждому платежу:

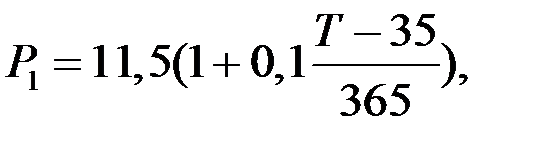
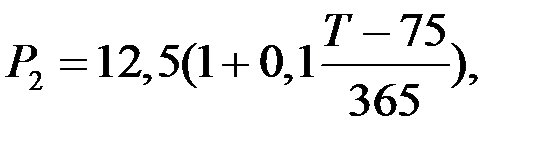
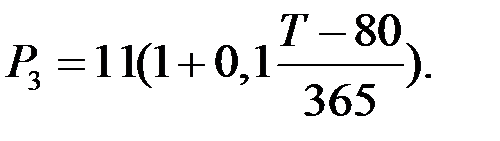
Сумма этих платежей должна составить величину консолидированного платежа:

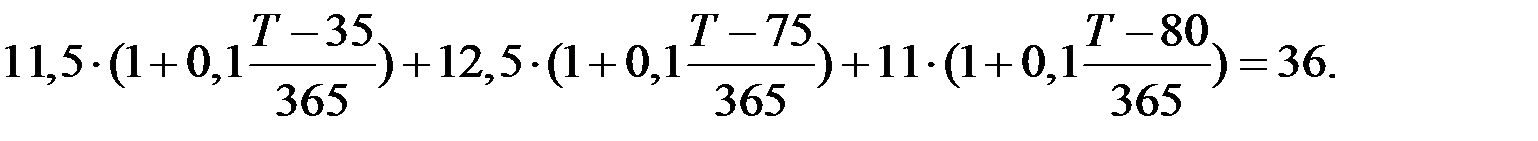
Решив данное уравнение относительно T, мы получаем Т=167,71=168 дней – срок консолидированного платежа.

Пример 17. Три платежа в 15000 руб., 26000 руб. и 45000 руб., произведенные в конце соответственно второго, третьего и пятого годов, заменить одним платежом 90000 руб. Годовая ставка сложных процентов равна 15%.

Для нахождения времени платежа 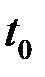приведём все три платежа к начальному моменту времени 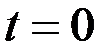и сложим их.

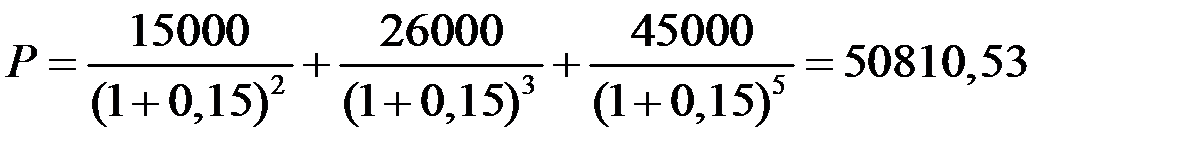руб.

По формуле (1.30) найдем искомое время .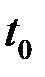

года.

1.6. Процентные ставки в условиях инфляции

При инфляции покупательная способность денег падает, так как цены на товары растут. Процесс, противоположный инфляции, называется дефляцией. Дефляция — повышение покупательной способности денег, что проявляется в снижении индекса цен. Темпом инфляции α называется отношение приращения стоимости корзины товаров за некоторый промежуток времени к стоимости корзины в начале периода:

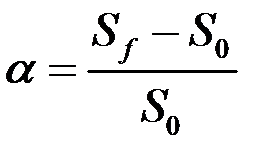, (1.31)

где 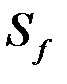- стоимость товара в конце расчетного периода, - стоимость товара в начале этого периода.

С темпом инфляции α связан индекс инфляции (индекс цен) I,равный I = 1+ α.

Если темп инфляции меняется несколько раз в году, то годовой темп инфляции вычисляется по формуле

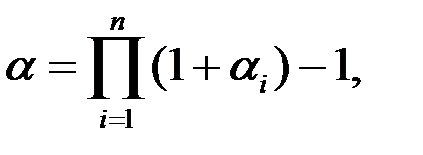(1.32)

где - темп инфляции за соответствующий период. Заметим, что темп инфляции за несколько периодов не равен алгебраической сумме темпов инфляции за соответствующие периоды.

Пример 18. Темп инфляции в январе, феврале и марте составил 1%, 2% и 3% соответственно. Найдите темп инфляции за первый квартал года.

Решение. Темп инфляции за несколько периодов найдём по формуле (1.28)

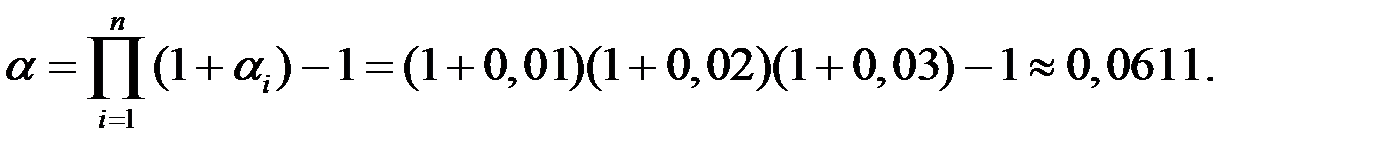
Таким образом, темп инфляции за три месяца составил приблизительно 6,11%.

Пример 19. Ожидаемый среднемесячный темп инфляции 2%. Найдите ожидаемый годовой темп инфляции.

Решение. Темп инфляции за несколько периодов найдём по формуле (1.28)

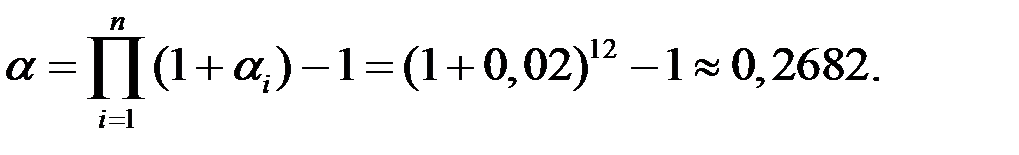
Следовательно, темп инфляции за год составит приблизительно 26,82 %.

При инфляции деньги обесцениваются в 1+ α раз. Поэтому покупательная способность наращенной суммы FV = PV (1 + r ), где r – номинальная процентная ставка, также уменьшится в 1+ α раз.

Реальная величина индекса вклада с учётом инфляции равна

(1.33)

Отсюда можно получить выражение и для реальной процентной ставки 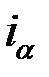(формула Фишера)

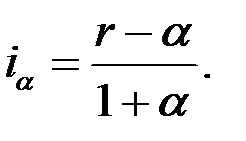(1.34)

Таким образом, для того чтобы номинальная процентная ставка r обеспечивала реальную процентную ставку 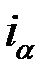при годовой инфляции α, она должна удовлетворять соотношению

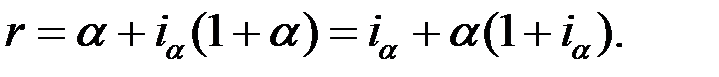(1.35)

Пример 20. Вкладчик рассчитывает получить 12 % реального дохода от годового депозита с учётом ожидаемого темпа инфляции 10% в год. Какова должна быть при этом номинальная процентная ставка?

Решение. Номинальную процентную ставку найдём по формуле (1.31)

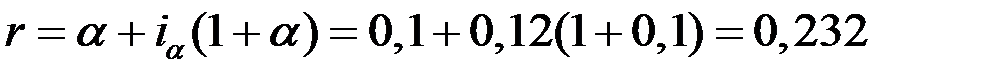или 23,2 %.

Пример21. Вкладчик открыл депозит на год под 14,4% годовых. Инфляция за год составила 10%. Найдите реальную процентную ставку.

Решение. Реальную процентную ставку найдём по формуле Фишера (1.30)

Таким образом, реальная ставка за год составила 4 %.

Депозиты с валютой

Помимо рублёвых депозитов, многие банки предлагают разместить денежные средства и в иностранной валюте, как правило, в долларах США или евро. Для резидентов, получающих доход в национальной валюте – рублях, для этого необходимо конвертировать рубли в одну или несколько из этих валют (мультивалютные депозиты).

Если, например, вклад открывается в долларах, то наращенная сумма FV (в долларах) при ежегодном начислении процентов равна

- в схеме простых процентов 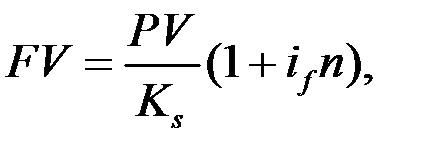(1.36)

- в схеме сложных процентов (1.37)

где PV – сумма вклада в рублях, – долларовая годовая процентная ставка, п - число лет (срок вклада), 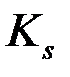- курс обмена валюты.

При конвертации наращенной суммы обратно в рубли нужно FV умножить на курс обмена валюты . Откуда можно найти и множитель наращения М рублёвых денежных средств

- в схеме простых процентов 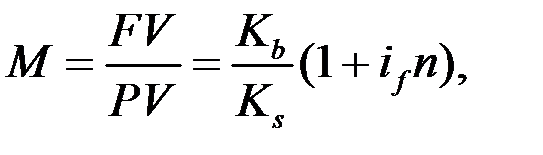(1.38)

- в схеме сложных процентов 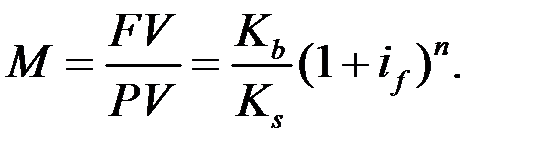(1.39)

Этот множитель можно сравнить с соответствующим множителем наращения для рублёвых депозитов с целью проверки эффективности приобретения валюты.

Задания для самостоятельной работы.

1. Банк открывает депозиты по ставке 10,5% годовых, предлагая различные схемы начисления сложного процента. Найдите величину вклада через два года при начислении сложного процента: а) 1; б) 4; в) 6; г) 12 раз в году, если начальная сумма вклада равна 10000 руб. Найдите величину вклада через два года при непрерывном начислении такого процента. Ответы округлите до рублей.

Ответ: а) 12271 руб.; б) 12303 руб.; в) 12314 руб.; г) 12326 руб. При непрерывном начислении процентов 12337 руб.

2. Банк предлагает различные схемы начисления сложного процента по ставке 12% годовых. На сколько процентов увеличится сумма вклада через три года при начислении сложного процента: а) 1; б) 4; в) 6; г) 12 раз в году? На сколько процентов увеличится сумма вклада через три года при непрерывном начислении такого процента?

Ответ: Приблизительно на а) 40,49 %; б) 42,58 %; в) 42,82 %; г) 43,08 %. При непрерывном начислении процентов приблизительно на 43,33%.

3. Найдите эффективную годовую процентную ставку для каждой схемы начисления сложных процентов задачи 2.

Ответ: а) ≈ 12 %; б) ≈ 12,55 %; в) ≈ 12,62 %; г) ≈ 12,68 %. При непрерывном начислении процентов .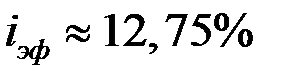

4. Депозит открывается на следующих условиях. В течение первых 120 дней банк начисляет 9 % годовых, в следующие 120 дней 10 % годовых и за последние 120 дней – 14 % соответственно (АСТ/360). Найдите эффективную процентную ставку.

Ответ: 11%.

5. Найти величину вклада, размещенного в банке на 4 года, если начальная величина вклада равна 1 млн. рублей. В первый год банк начислял 10% годовых ежемесячно, а в оставшиеся три года – 8% годовых ежеквартально.

Ответ: 1401043,28 рублей.

6. Найдите непрерывную процентную ставку 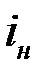, эквивалентную сложной процентной ставке.

Ответ: 44,88%

7. Найдите сложную процентную ставку , эквивалентную непрерывной процентной ставке 8%.

Ответ: 8,33%

8. Найдите простую процентную ставку 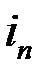, эквивалентную сложной ставке в 7% для временного интервала в 6 лет при ежеквартальном начислении процентов.

Ответ: 8,6%

9. За сколько лет произойдёт удвоение капитала при начислении сложных процентов раз в год по процентной ставке 7%?

Ответ: ≈ 10 лет.

10. Найдите количество лет, за которое начальный капитал увеличится в N раз при непрерывном начислении сложного процента i.

Отв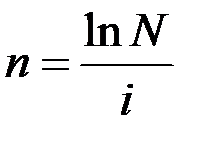ет: лет.

11. Для каждой схемы начисления сложных процентов задачи 2 найдите сумму, которую нужно положить в банк, чтобы через три года сумма вклада стала равной 1 млн руб. Ответы округлите до рублей.

Ответ: а) 711780 руб.; б) 701380 руб.; в) 700159руб.; г) 698925 руб. При непрерывном начислении процентов 697676 руб.

12. Вексель стоимостью 1,5 млн. руб. учитывается за два года до погашения по а) простой; б) сложной учётной ставке 12% годовых. Найдите сумму, которую получит векселедержатель, и величину дисконта.

Ответ: а) 1140000 руб., 360000 руб., б) 1161600 руб., 338400 руб.

13. Вексель учитывается под 10% годовых за три года до погашения. Хватит ли векселедержателю полученных средств, чтобы погасить вексель, если он поместит их на депозит под 11% годовых? Изменится ли ответ, если изменить число лет до погашения?

Ответ: Нет, нет.

14. Три платежа 20000 руб., 40000 руб. и 70000 руб., которые нужно произвести в конце первого года, четвертого и шестого года, замените одним платежом 120000 руб.

Ответ: 3,26 года.

15. Три платежа 15000 руб., 25000 руб. и 45000 руб., произведенные соответственно в начале второго, третьего и шестого годов, замените двумя платежами в конце седьмого и девятого годов, считая, что первый платёж в 5 раз меньше второго. Годовая ставка сложных процентов равна 19%. Ответ округлите до рублей.

Ответ: 36633 руб. и 183167 руб.

16. Кредит в размере 100000 рублей необходимо погасить через 6 лет. На основе сложной ставки 10% годовых решено изменить порядок оплат. Задолженность погашается тремя равными частями S через год, три и пять лет. Чему равно S .

Ответ: 24743 руб.

17. Ожидаемый годовой темп инфляции 36%. Найдите ожидаемый среднемесячный темп инфляции.

Ответ: ≈ 2,6%.

18. Ожидаемый среднемесячный темп инфляции 3%. Найдите ожидаемый квартальный темп инфляции.

Ответ: 9,27%.

19. Ожидаемый годовой темп инфляции 36%. В течение первых трёх месяцев года темп инфляции составил 1%, 3% и 4% соответственно. Найдите, каким должен быть среднемесячный темп инфляции за оставшиеся месяцы, чтобы к концу года выйти на ожидаемые годовые показатели?

Ответ: ≈ 2,57%.

20. Найдите реальную процентную ставку с учетом инфляции, если на вклад, открытый в банке на 1 год, начисляются 17 % в конце года. Темп инфляции в первом полугодии составил 6%, во втором – 8%.

Ответ: 2,2 %.

21. Найдите реальную процентную ставку с учетом инфляции, если на вклад, открытый в банке на 1 год под 10 % годовых, проценты начисляются ежемесячно. Темп инфляции в первом полугодии составил 4%, во втором – 5%.

Ответ: 1,16%.

Тема 2. Потоки платежей.

Финансовые потоки платежей.

С разовыми платежами человек имеет дело, если совершает покупки, оплачивает услуги или получает бонусы. В большинстве экономических процессов участники фигурируют в целой серии однородных платежей, к примеру получение заработной платы, стипендий, пенсий, оплата коммунальных услуг, инвестирование средств в производство с последующим получением прибыли, налоговые, арендные платежи и прочие регулярные поступления и расходы денег.

Назовём (мгновенным) финансовым событием пару 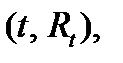где 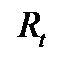- величина платежа в момент времени 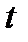, где 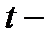время платежа.

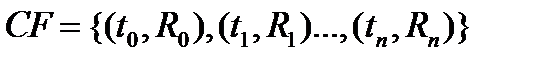
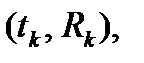
Потоком платежей или финансовым потоком (cash flow ) назовём последовательность финансовых событи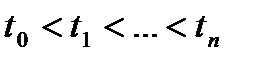й

и .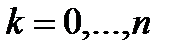

В дальнейшем, если не будет оговорено противное, будем рассматривать конечные потоки платежей.

Текущимзначением ( present value ) потока платежей , приведённым к моменту времени называется величина

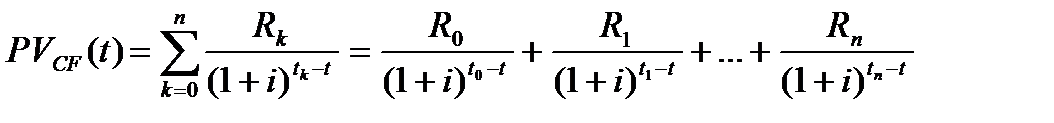, (2.1)

которая является суммой значений всех платежей потока, приведённых (дисконтированных) к моменту времени 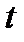по процентной ставке .

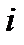Текущее значение потока при 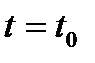называется начальной величиной потока:

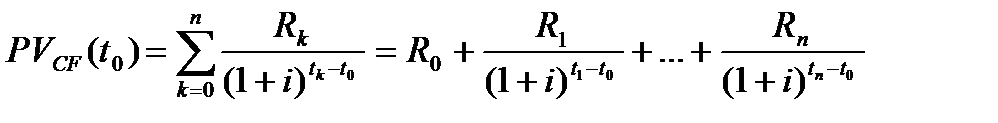(2.2)

При 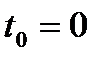будем 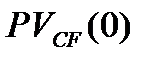обозначатьпросто 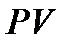и называть современной (приведённой) величиной потока

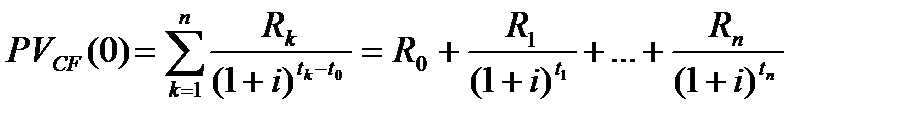(2.3)

Будущим (накопленным, наращенным)значением ( future value ) финансового потока 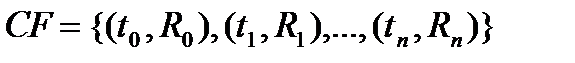в момент времени называется величина

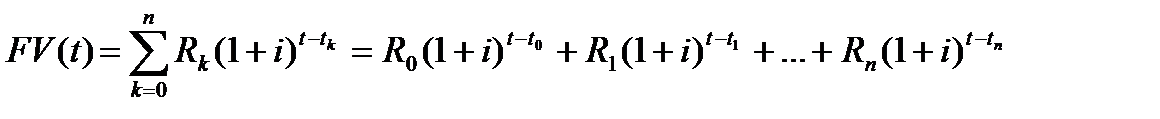(2.4)

Конечная величина потока 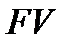равна его будущему значению при 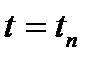: 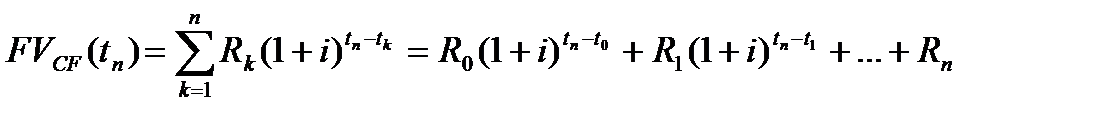(2.5)

Пример 1. Вычислить современную и конечную величины следующего потока: 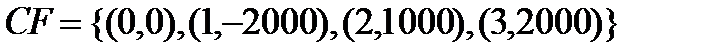при i=10%.

Решение. Воспользуемся (2.3) и (2.5), тогда

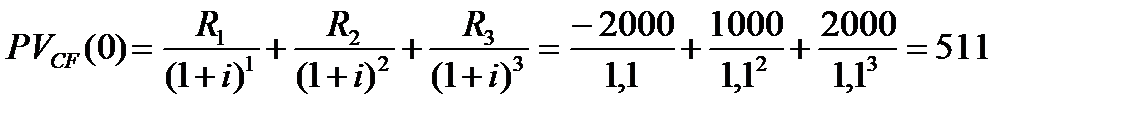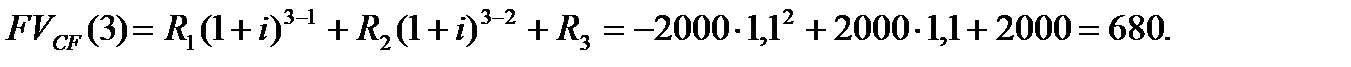
Пример 2. Платежи 1 млн. руб.; 2млн. руб. и 3 млн. руб. со сроками уплаты соответственно через 1; 2 и 3 года объединяются в один через 4 года. Консолидация проводится по сложной ставке 10% годовых. Определить консолидированный платеж.

Решение. Величина консолидированного платежа находится согласно (2.4) как величина (в млн. руб.) соответствующего финансового потока 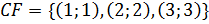, приведённая к моменту времени t =4 : млн.руб.

Пример 3. Имеется переменный финансовый поток 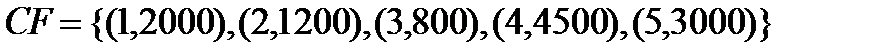. Рассчитайте приведенную стоимость финансового потока, если начисления процентов осуществляется по сложной процентной ставке 25% годовых.

Решение: n=5, 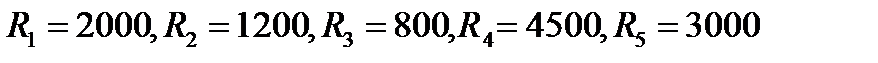. Тогда с учетом (2.3) найдем

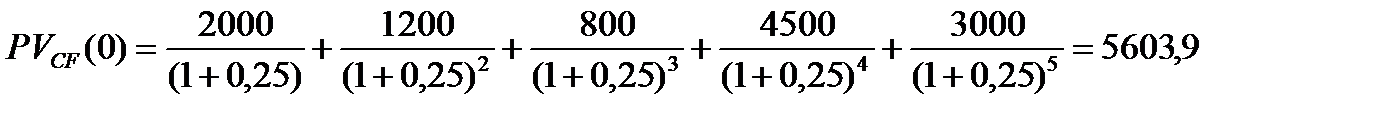руб.

Средним сроком финансового потока 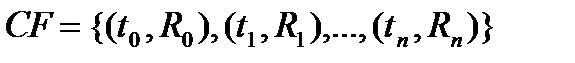(относительно ставки дисконтирования 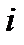) называется значение времени 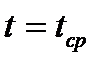, для которого текущая величина потока в момент 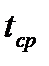равна сумме всех платежей

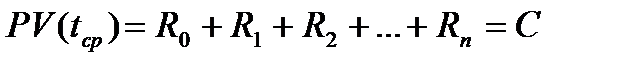(2.6)

Из (2.6) c учетом (2.4) следует формула для среднего срока потока:

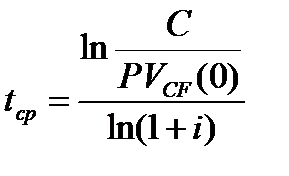, (2.7)

где .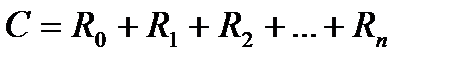

Заметим, что в случае 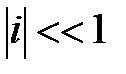, формула может быть упрощена и записана в виде

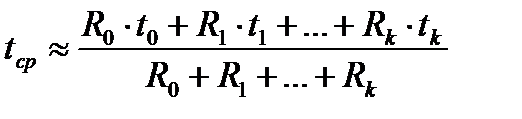
Пример 4. Определите средний срок потока платежей при i =10%: .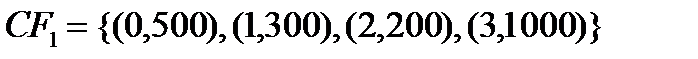

Решение. По формуле (2.3) вычислим 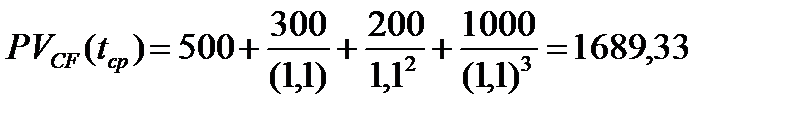руб. и 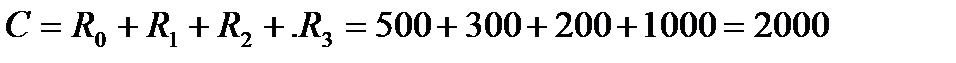руб. С учетом полученных значений и (2.7) получим

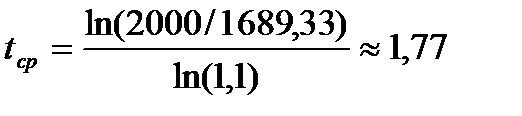лет.

2.1.2.Поток платежей инвестиционного проекта

Опр. Под инвестированием в общем случае понимается вложение денежных средств (инвестиций)в какой-либо проект с целью получения через некоторое время прибыли. Инвестиционные проекты характеризуются «растянутостью» и нерегулярностью во времени: доходы от инвестиций могут проявляться не сразу, но поступают в течение достаточно длительного срока.

Поток платежей инвестиционного проекта — это совокупность планируемых поступлений и выплат денежных средств, которые имеют непосредственное отношение к данному проекту.

Отрицательные платежи в этом потоке соответствуют вложениям инвестора в проект, положительные — его доходам.

Рассмотрим конечный финансовый поток, 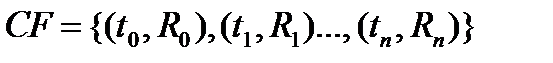. В этом случае приведенную величину потока 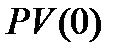часто называют чистой приведенной стоимостью (net present value, NPV), равный сумме приведенных величин всех платежей (как положительных , так и отрицательных)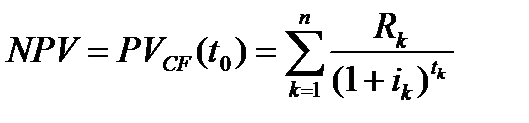

Считается, что вкладывать деньги в проект, порождающий такой поток , выгодно, если его .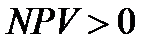

Пример 5.Сравните два потока и 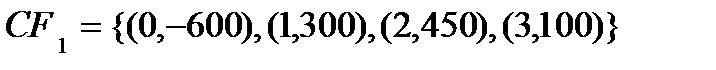по NPV для ставки дисконтирования в 10%.

Решение. Согласно введеного выше определения получим

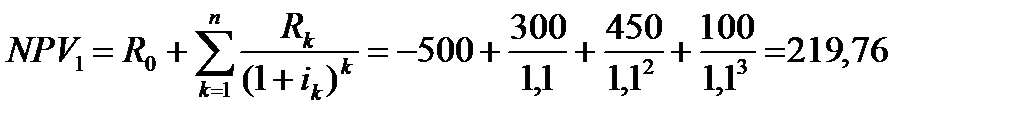
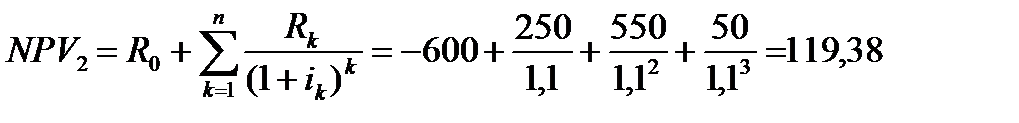
Отсюда следует, что 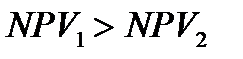, первый проект более привлекателен по параметру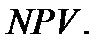

Другой важной характеристикой в теории инвестиций является внутренняя норма доходности.

Под внутренней нормой доходности понимают значение коэффициента дисконтирования IRR, при котором чистый приведенный доход (NPV) проекта равен нулю, и он находится из уравнения

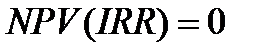
Внутренняя норма доходности - IRR определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника т.е. .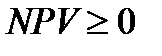

Пример 6. Вычислить внутреннюю норму доходности финансового потока

CF ={(0; -50),(2; 25),(4;150)}.

Решение. Внутренняя норма доходности определяется как ставка дисконтирования IRR, при которой NPV=0.

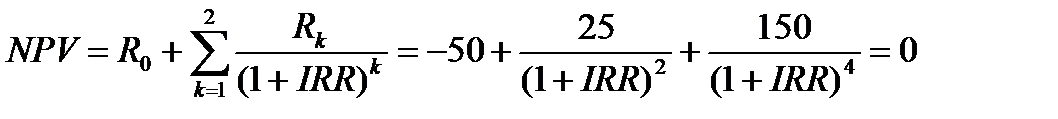
Таким образом, для нахождения нормы доходности нам необходимо решить данное уравнение. Сделаем замену , тогда уравнение принимает вид 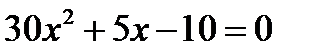. Из решения данного квадратного уравнения получим 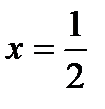. С учетом замены находим 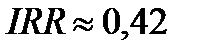, т.е. внутренняя норма доходности данного проекта более 42%.

В общем случае поиск IRR может быть выполнен только численно , например с помощью Excel.

Дата добавления: 2020-04-08; просмотров: 2857; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!