Основные понятия портфельного анализа.
Портфелем, состоящим из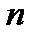 
видов активов 
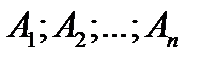будем называть вектор : 
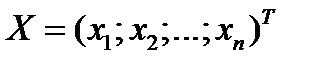(здесь 
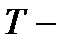транспонирование), где 
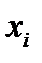- доля (весовой коэффициент) инвестиций в ценные бумаги вида 
, 
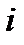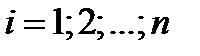в стоимостном выражении.
Очевидно, что для любого портфеля выполнено условие нормировки.
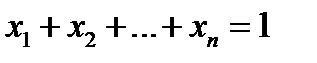или 
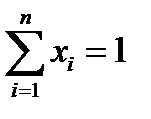
Если значения 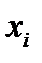, 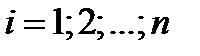могут быть любого знака, то такая модель называется моделью Блэка. Если же 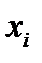, 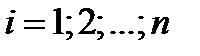принимают только неотрицательные значения, то такая модель называется моделью Марковица.
Если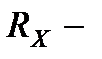 
доходность портфеля 
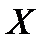, то
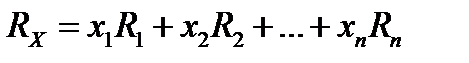, (4.1)
где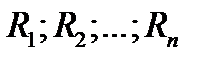 
- доходности ценных бумаг, входящих в портфель .
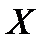Математическое ожидание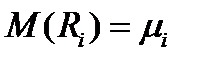 
доходности актива 
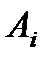называется ее ожидаемой доходностью, а математическое ожидание 
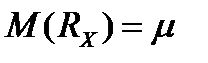доходности портфеля 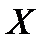называется ожидаемой доходностью портфеля 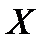. Из (4.1) следует, что:
,
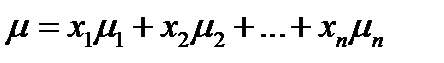где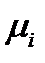 
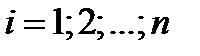, , - ожидаемые доходности бумаг вида 
.
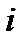Обозначим через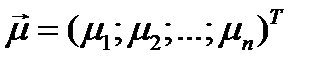 
вектор ожидаемых доходностей бумаг портфеля 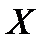. Тогда ожидаемая доходность портфеля 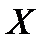будет равна:
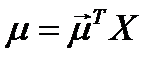(4.2)
Дисперсия (квадратичный риск) доходности бумаги вида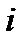 
равна:
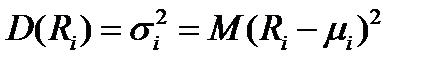
Риск бумаги вида 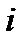определяется как среднеквадратическое отклонение (СКО) ее доходности: 
.
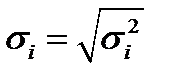Ковариация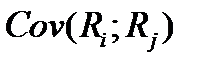 
доходносте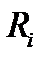й 
и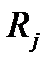 
бумаг вида 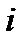и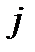 
равна:
.
При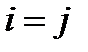 
:
.
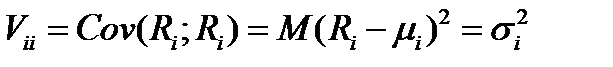Матрица
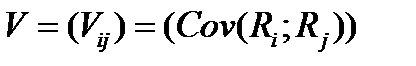(4.3)
|
|
|
называется ковариационной матрицей.
Коэффициент корреляции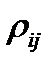 
доходностей бумаг вида 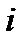и 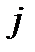равен:
.
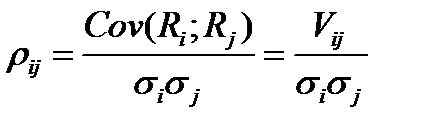Матрица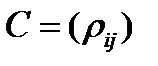 
называется корреляционной матрицей.
Ковариационная матрица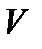 
и корреляционная матрица 
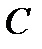являются симметричным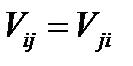и: 
и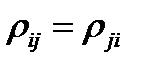 
. Так как
,
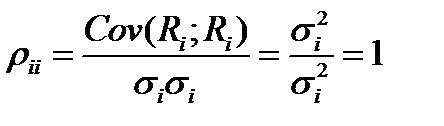то на главной диагонали матрицы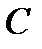 
расположены единицы.
Дисперсия доходности (квадрат риска) портфеля ценных бумаг равна:
.
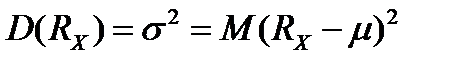Можно показать, что
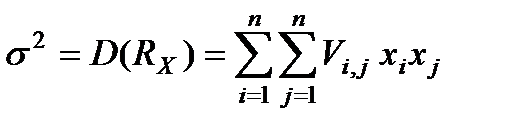(4.4)
В матричном виде это выражение имеет вид:
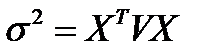(4.5)
Риск портфеля равен:
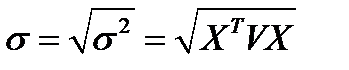(4.6)
Таким образом, каждому портфелю 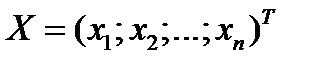можно поставить в соответствие его оценку - пару чисел 
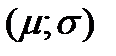, где 
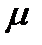- ожидаемая доходность портфеля, 
- риск портфеля.
При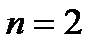 
ковариационная и корреляционная матрицы имеют вид
,
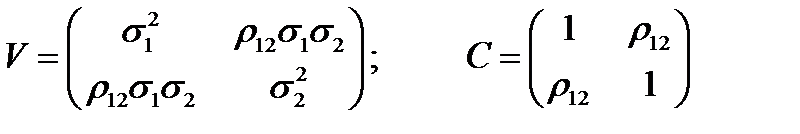а для портфеля из трех бумаг
.
Пример 1. Дана ковариационная матрица:
.
Найти корреляционную матрицу.
Решение. Риски бумаг равны: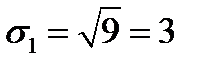 
; 
; 
.
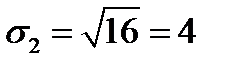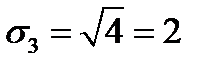Коэффициенты корреляции равны:
; 
; 
.
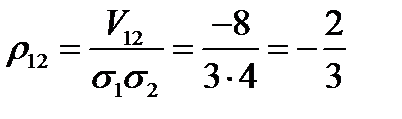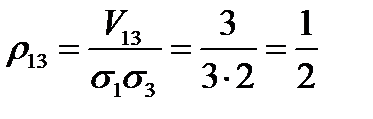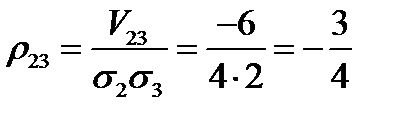Ответ. Корреляционная матрица имеет вид:
|
|
|
.
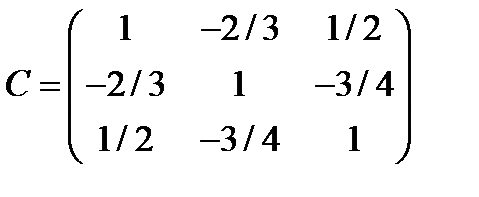Пример 2. Дана ковариационная матрица двух активов: 
. Найти корреляционную матрицу.
Решение.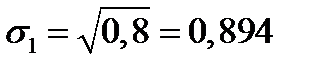 
; 
; 
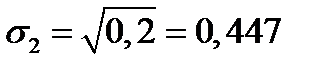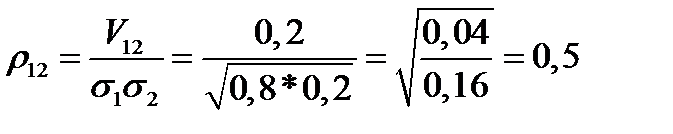
Ответ. 
.
Пример 3. Дана ковариационная матрица трех активов: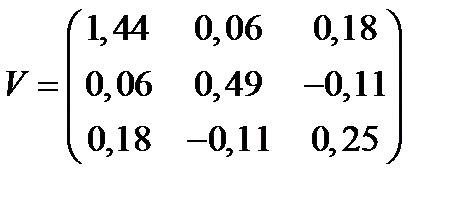 
. Найти корреляционную матрицу.
Решение.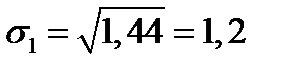 
; 
; 
.
; 
; 
.
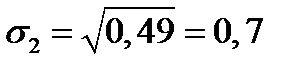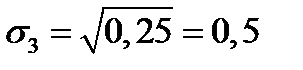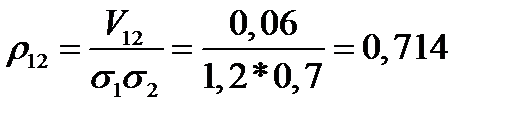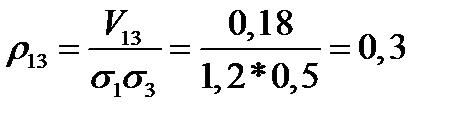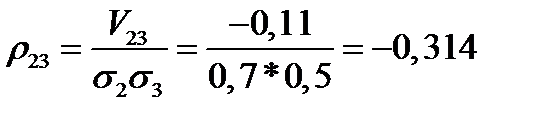Ответ. Корреляционная матрица равна: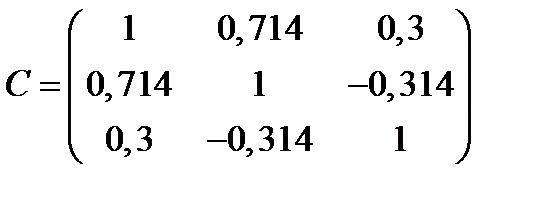 
Пример 4. Ценовыедолиактивовв портфеле относятся как 3:2. Ожидаемые доходности активов равны: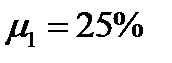 
, 
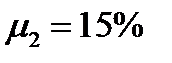. Ковариационная матрица равна: 
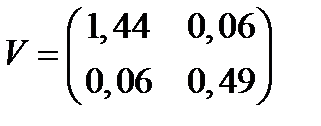. Найти портфель, его ожидаемую доходность и риск.
Решение. Ценовыедолиактивовв портфеле равны: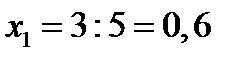 
, 
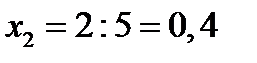. Портфель равен: 
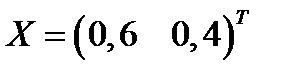. Вектор ожидаемых доходностей равен: 
.
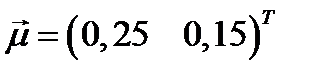Ожидаемая доходность портфеля равна
.
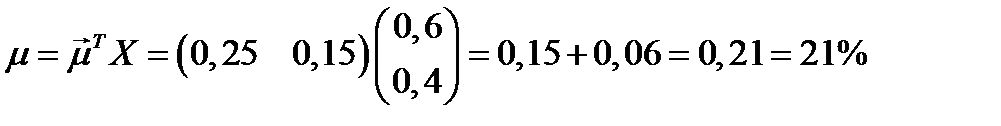Квадрат риска портфеля равен
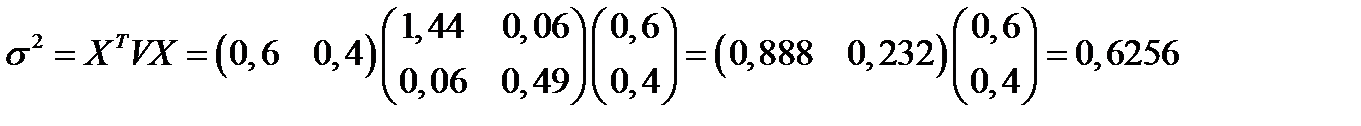
Риск портфеля равен
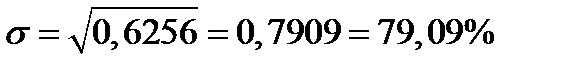
Ответ. ;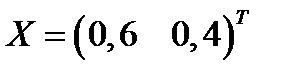 
; 
.
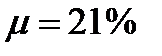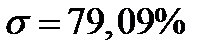Пример 5. Ценовыедолиактивовв портфеле относятся как 2:3:5. Ожидаемые доходности активов равны: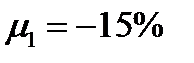 
, 
, 
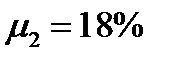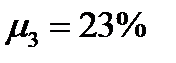. Ковариационная матрица равна: 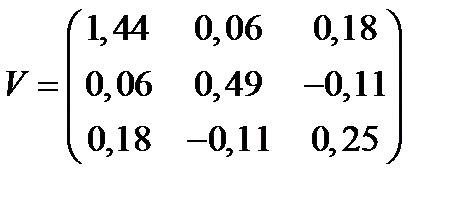. Найти портфель, его ожидаемую доходность и риск.
Решение. Ценовыедолиактивовв портфеле равны: 
, 
, 
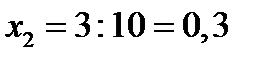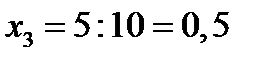. Портфель равен: 
.
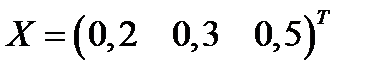Вектор ожидаемых доходностей равен: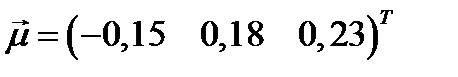 
.
Ожидаемая доходность портфеля равна:
.
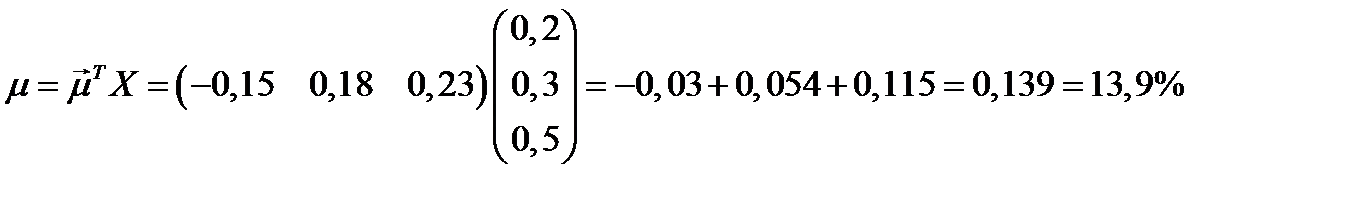Квадрат риска портфеля равен:
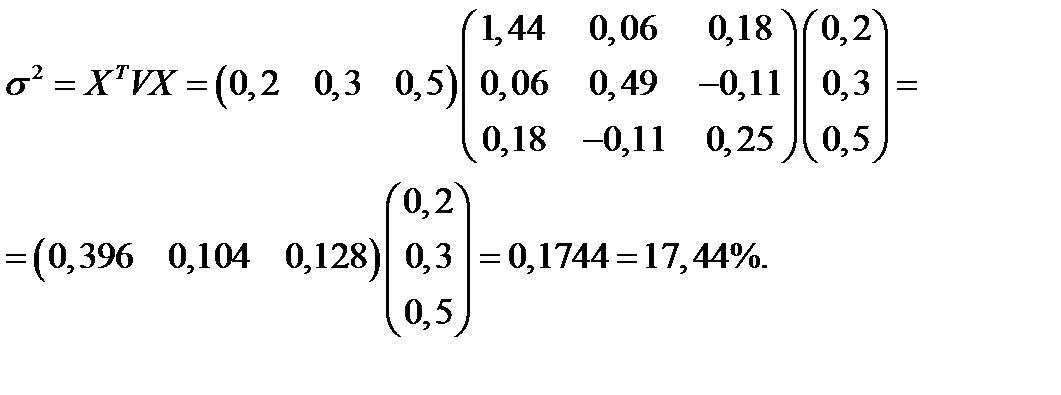
Риск портфеля равен:
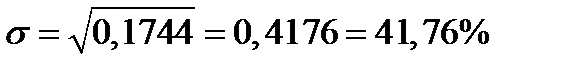
Ответ. ;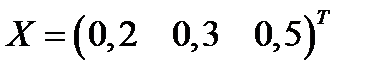 
; 
.
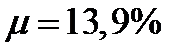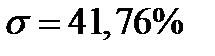Портфель, для которого в заданном множестве портфелей не найдется портфеля, имеющего оценку с большей доходностью при равном или меньшем риске, или оценку с меньшим риском при равной или большей доходности, называется эффективным портфелем относительно этого множества.
|
|
|
Пример 6. Пусть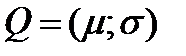 
- оценка портфеля. Рассмотрим 4 портфеля с оценками:
, 
, 
, 
.
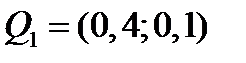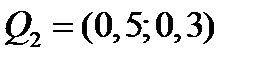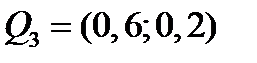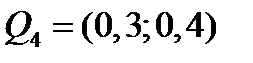Третий портфель имеет наибольшую доходность, а первый портфель имеет наименьший риск. Эффективными относительно заданного множества из четырех портфелей являются только первый и третий портфели.
Наилучшим портфелем из заданного множества портфелей называется портфель, имеющий наибольшую доходность и наименьший риск среди всех заданных (допустимых) портфелей.
Пример №7. Рассмотрим 4 портфеля с оценками:
, 
, 
, 
.
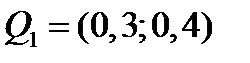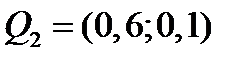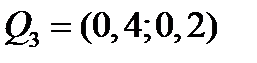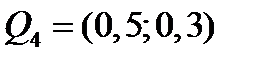Из заданного множества портфелей наилучшим является второй, так как он имеет наибольшую доходность и наименьший риск.
Введя координатную плоскость 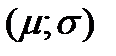и вычисляя для каждого портфеля из допустимого множества портфелей его оценку 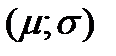, можно отобразить оценки всех допустимых портфелей точками на этой плоскости (называемой плоскостью оценок).
Образом допустимого множества портфелей при таком отображении будет некоторое множество в плоскости оценок, которое называется критериальным множеством.
Можно показать, что оценки эффективных портфелей лежат на границе критериального множества.
|
|
|
Множество оценок всех эффективных портфелей называется эффективной границей критериального множества или Парето-эффективной границей (кривая Парето) .
Портфели ценных бумаг, состоящие из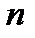 
рисковых бумаг, называются портфелями Марковица.
Основными задачами портфельного анализа являются:
- найти портфель минимального риска при заданной его доходности, или при доходности не меньшей заданной, или при произвольной доходности;
- найти портфель максимальной доходности при минимальном риске или при риске, не превышающем заданный уровень.
Дата добавления: 2020-04-08; просмотров: 770; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!