Портфель Тобина минимального риска из всех портфелей с заданной ожидаемой доходностью
Требуется найти портфель 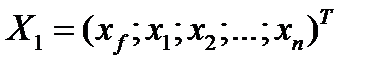 , который минимизировал бы риск
, который минимизировал бы риск  и обеспечивал заданную величину
и обеспечивал заданную величину 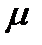 ожидаемой доходности.
ожидаемой доходности.
Следовательно, постановка задачи такова: найти минимум целевой функции
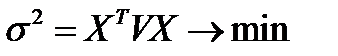
при условиях:
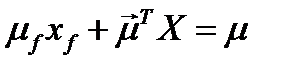 ,
,
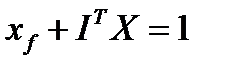 ,
,
где 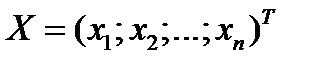 .
.
Умножим нижнее уравнение на 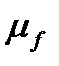 :
:
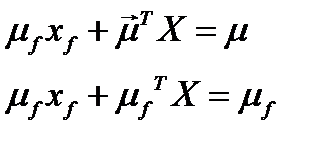
и исключим переменную 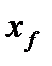 из уравнений, вычитая из верхнего уравнения нижнее. Получим уравнение:
из уравнений, вычитая из верхнего уравнения нижнее. Получим уравнение:
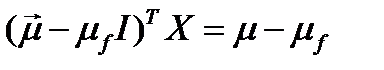 .
.
Задача оптимизации примет следующий вид: найти минимум целевой функции
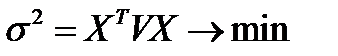
при условии:
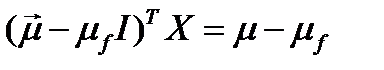 .
.
Для решения этой задачи составим функцию Лагранжа и запишем для нее необходимые условия экстремума:
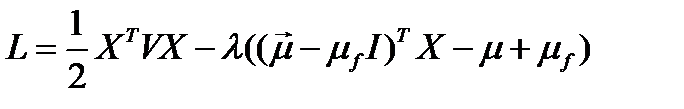 .
.
Необходимые условия экстремума имеют вид:
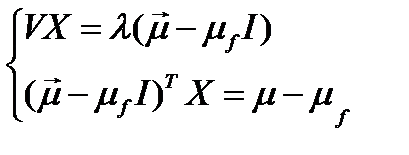 .
.
Выразим 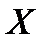 из первого уравнения и подставим во второе:
из первого уравнения и подставим во второе:
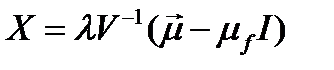 ;
;
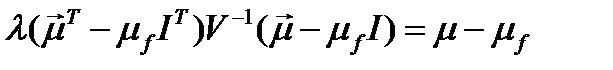
или
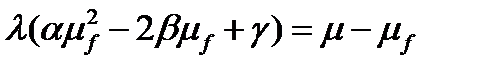 .
.
Множитель Лагранжа равен:
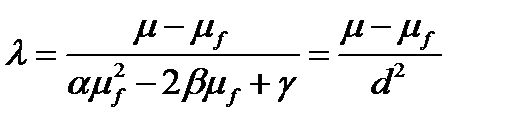 ,
,
где
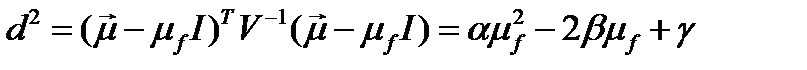
и
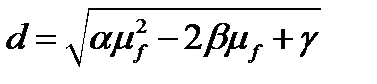 .
.
Вектор рисковых долей равен:
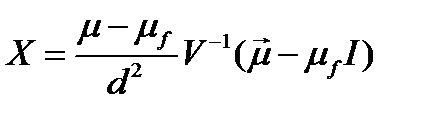 .
.
Безрисковая доля равна:
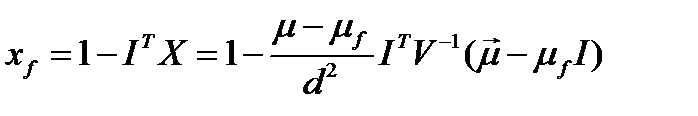 .
.
Квадрат минимального риска равен:
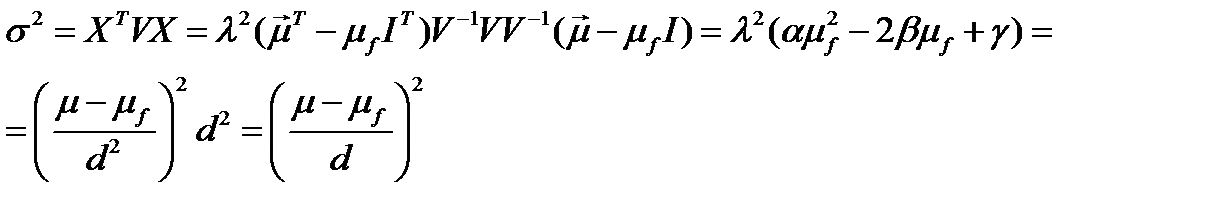
Так как 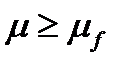 , то уравнение минимальной границы портфеля Тобина имеет вид:
, то уравнение минимальной границы портфеля Тобина имеет вид:
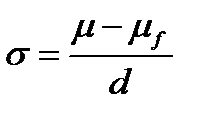 .
.
Можно показать, что эта прямая является касательной к графику минимальной границы портфеля Марковица:
 .
.
Координаты точки касания равны:
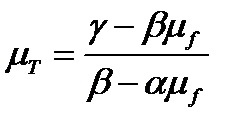 ;
; 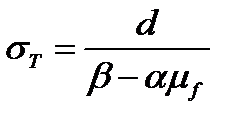 .
.
При этом сам касательный портфель равен:
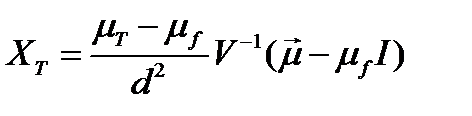 .
.
Включение безрискового актива в портфель на практике отвечает возможности занимать или давать в долг финансовые ресурсы по безрисковой ставке.
Безрисковый актив, входящий в портфель с положительной долей означает, например, покупку государственных облигаций. Безрисковый актив, входящий в портфель с отрицательной долей, может означать заем по безрисковой ставке. Включение в портфель безрискового актива существенно упрощает множество эффективных портфелей (рис. 4.3).
|
|
|
Рис.4.3. Множество эффективных портфелей Тобина.
Множеством эффективных портфелей является полупрямая 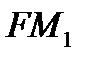 . Эффективные портфели составляются из безрискового актива
. Эффективные портфели составляются из безрискового актива 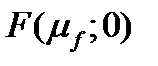 и касательного портфеля
и касательного портфеля 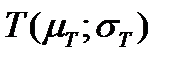 . Полупрямая
. Полупрямая 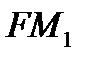 состоит из точек:
состоит из точек:
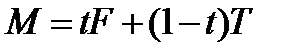 .
.
Если 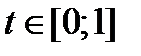 , то эффективным множеством портфелей является отрезок
, то эффективным множеством портфелей является отрезок 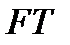 .
. 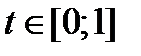 соответствует наличию в портфеле безрисковой бумаги.
соответствует наличию в портфеле безрисковой бумаги.
Если 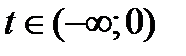 , то эффективным множеством портфелей является полупрямая
, то эффективным множеством портфелей является полупрямая 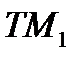 .
. 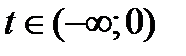 соответствует заимствованию финансовых ресурсов в долг по безрисковой ставке.
соответствует заимствованию финансовых ресурсов в долг по безрисковой ставке.
Пример 15. На рынке присутствуют три актива: безрисковый с доходностью 5% и два рисковых с ожидаемыми доходностями 10% и 20% и ковариационной матрицей 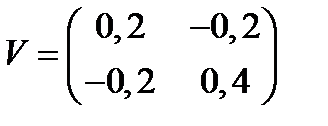 . Найти портфель Тобина минимального риска с ожидаемой доходностью 12% и риск этого портфеля.
. Найти портфель Тобина минимального риска с ожидаемой доходностью 12% и риск этого портфеля.
Решение. Вектор рисковых долей в портфеле равен:
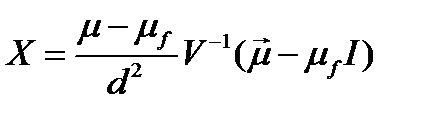 ;
;
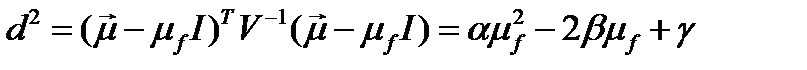 .
.
Здесь 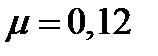 - заданная доходность портфеля Тобина,
- заданная доходность портфеля Тобина, 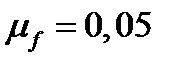 - доходность безрискового актива,
- доходность безрискового актива, 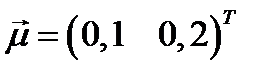 - вектор ожидаемых доходностей рисковых бумаг,
- вектор ожидаемых доходностей рисковых бумаг, 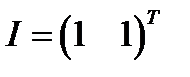 .
.
Обратная матрица равна:
|
|
|
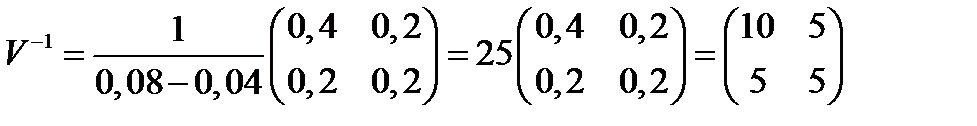 .
.
Вычислим параметры 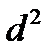 и
и 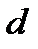 :
:
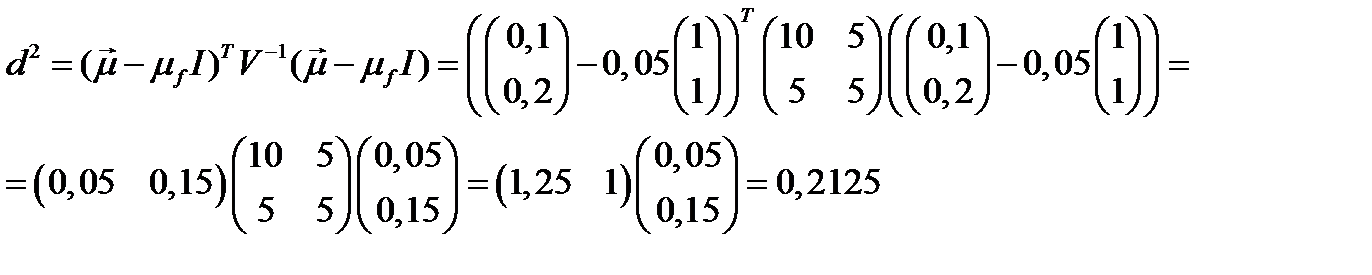
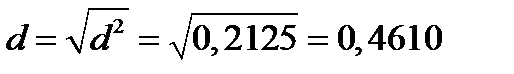 .
.
Вектор рисковых долей в портфеле равен:
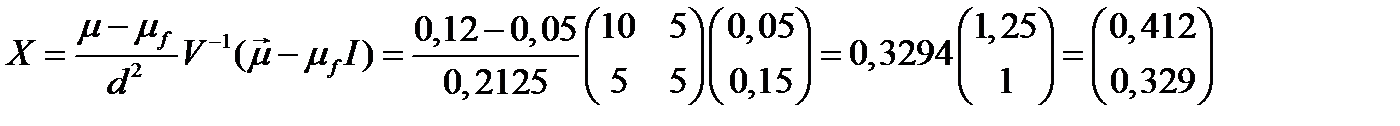
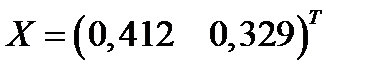 .
.
Ценовая доля безрисковой бумаги равна:
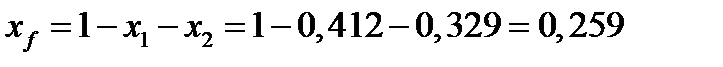 .
.
Портфель Тобина ожидаемой доходности 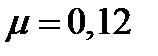 имеет вид:
имеет вид:
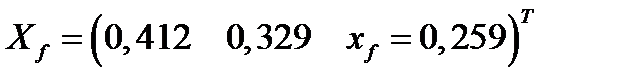 .
.
Квадрат риска портфеля равен:
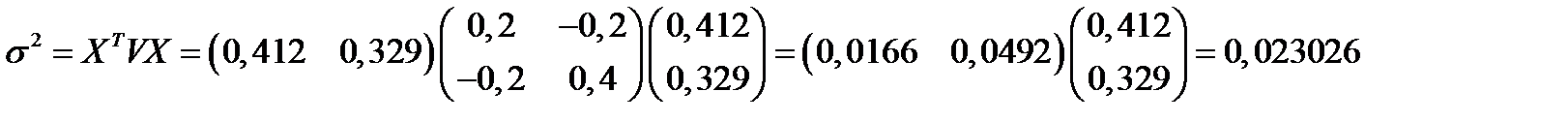 .
.
Риск портфеля равен:
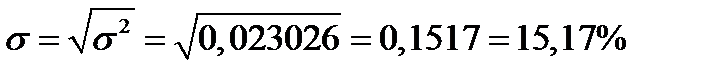 .
.
Ответ. 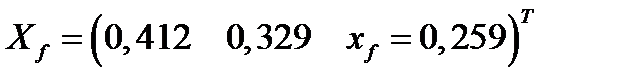 ;
; 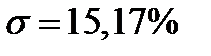 .
.
Пример 16. На рынке присутствуют три актива: безрисковый с доходностью 3% и два рисковых с ожидаемыми доходностями 10% и 20% и ковариационной матрицей 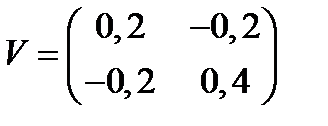 . Найти касательный портфель и его ожидаемую доходность и риск.
. Найти касательный портфель и его ожидаемую доходность и риск.
Решение. Касательный портфель 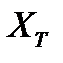 имеет вид:
имеет вид:
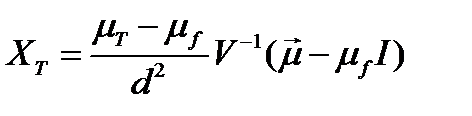 .
.
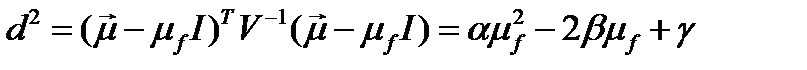 .
.
Здесь 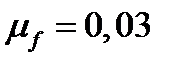 - доходность безрискового актива,
- доходность безрискового актива, 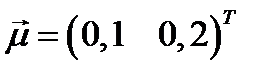 - вектор ожидаемых доходностей рисковых бумаг,
- вектор ожидаемых доходностей рисковых бумаг, 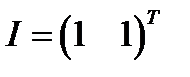 .
.
Обратная матрица равна:
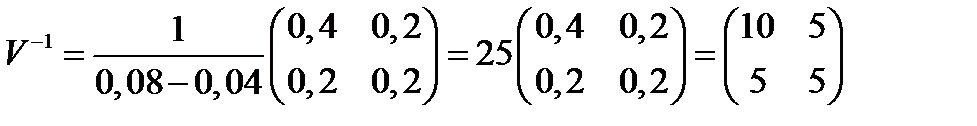 .
.
Вычислим параметры 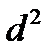 и
и 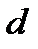 :
:
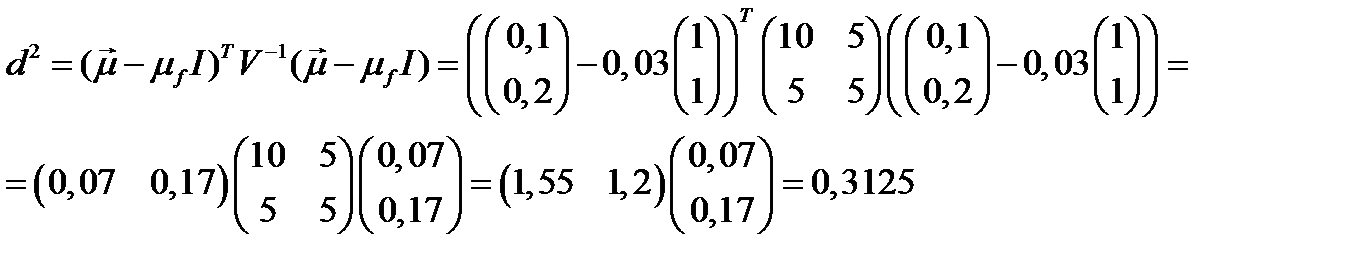
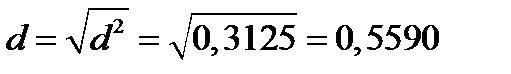 .
.
Значения ожидаемой доходности 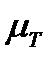 и риска
и риска 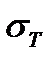 касательного портфеля равны:
касательного портфеля равны:
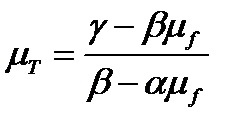 ;
; 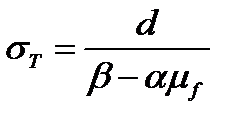 .
.
Найдем значения констант:
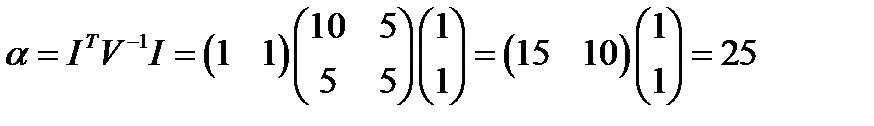 ;
;
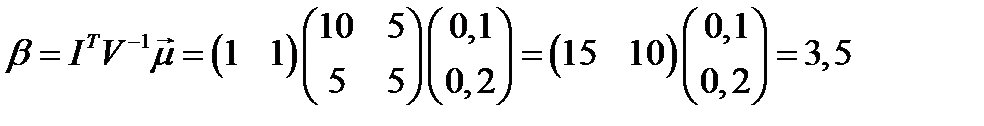 ;
;
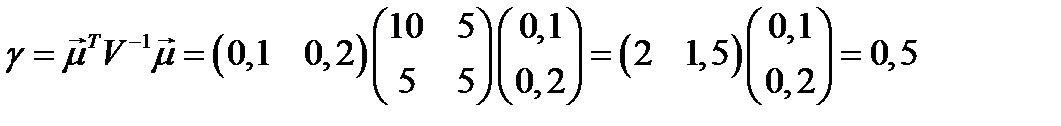
Теперь найдем значения ожидаемой доходности 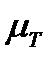 и риска
и риска 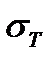 касательного портфеля:
касательного портфеля:
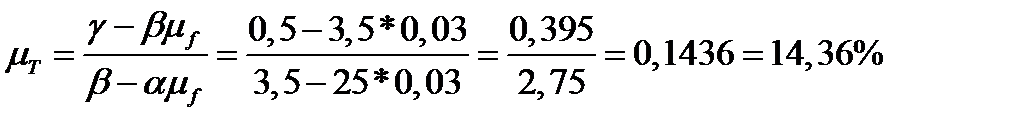 ;
;
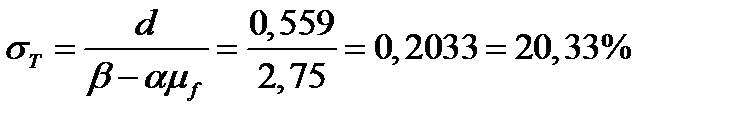 .
.
Искомый касательный портфель равен:
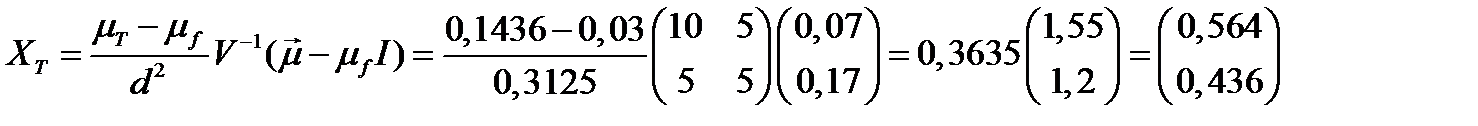 .
.
Касательный портфель ожидаемой доходности 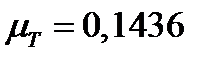 и риска
и риска 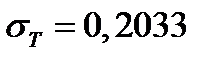 имеет вид:
имеет вид:
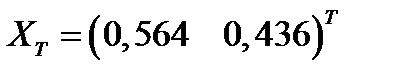 .
.
Ответ. 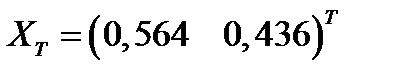 ;
; 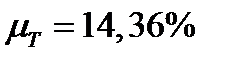 ;
; 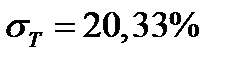 .
.
Пример 17. Дано уравнение минимальной границы: 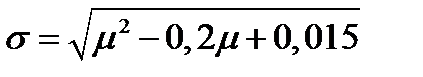 . Безрисковая доходность равна 0,05. Найти ожидаемую доходность и риск касательного портфеля.
. Безрисковая доходность равна 0,05. Найти ожидаемую доходность и риск касательного портфеля.
Решение. Уравнение минимальной границы имеет вид:
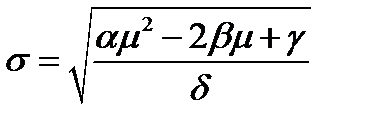 .
.
Следовательно, справедливы соотношения: 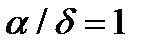 ;
; 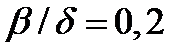 ;
; 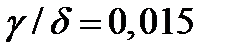 .
.
|
|
|
Выражая 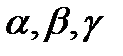 через
через 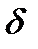 , получаем:
, получаем: 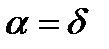 ,
, 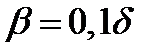 и
и 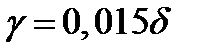 .
.
Подставляя полученные выражения в формулу 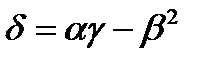 , получаем уравнение для нахождения
, получаем уравнение для нахождения 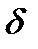 :
:
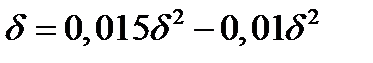 .
.
Решая его, находим 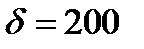 и, следовательно,
и, следовательно, 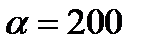 ,
, 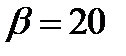 ,
, 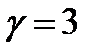 .
.
Так как доходность безрискового актива 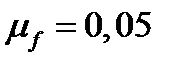 , ожидаемая доходность касательного портфеля равна:
, ожидаемая доходность касательного портфеля равна:
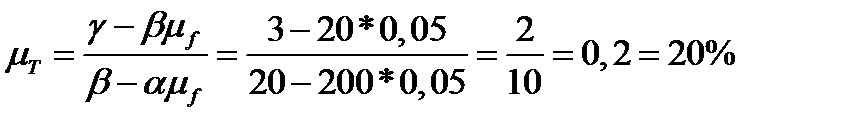 .
.
Найдем параметр 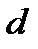 :
:
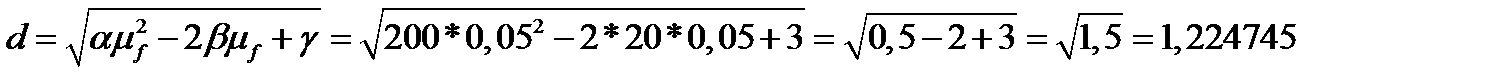 .
.
Риск касательного портфеля равен:
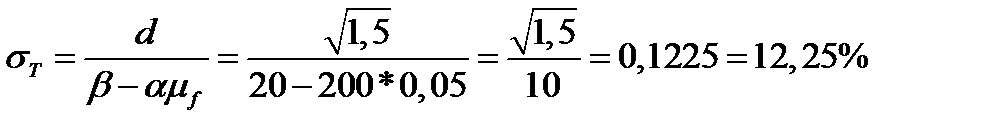 .
.
Ответ. 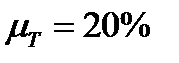 ,
, 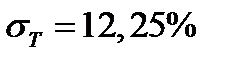 .
.
4.6.2. Портфель Тобина максимальной доходности из всех портфелей риска не более заданного значения 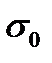
Требуется найти максимальное значение целевой функции:
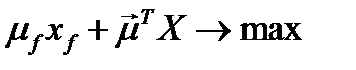
при условиях: 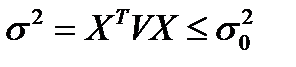 ,
,
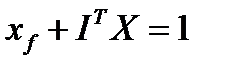 .
.
Решим данную задачу графически. На рис.4.4 изобразим эффективную границу портфеля Тобина:
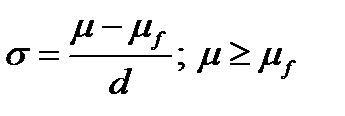
и граничную прямую 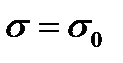 . Так как по условию:
. Так как по условию: 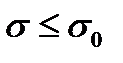 , то портфель максимальной доходности, удовлетворяющий этому условию, будет в точке пересечения луча
, то портфель максимальной доходности, удовлетворяющий этому условию, будет в точке пересечения луча
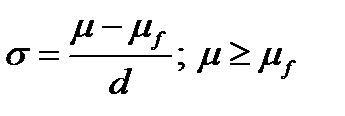
и прямой 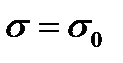 .
.
Рис. 4.4. Определение максимальной доходности портфеля 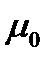 .
.
Таким образом, 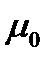 находится из уравнения:
находится из уравнения:
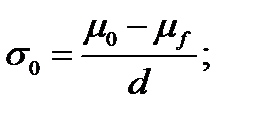
Откуда: 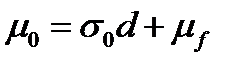 и
и 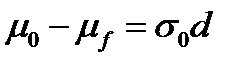 .
.
Зная 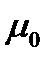 можно найти соответствующий рисковый портфель
можно найти соответствующий рисковый портфель
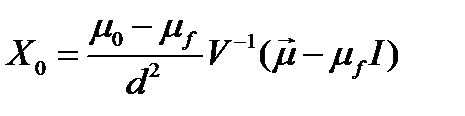 или
или 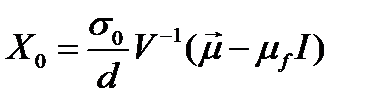
и долю безрискового актива в портфеле Тобина:
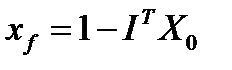 .
.
Пример 18. На рынке присутствуют три актива: безрисковый с доходностью 5% и два рисковых с ожидаемыми доходностями 10% и 20% и ковариационной матрицей 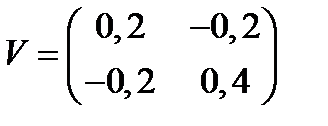 . Найти портфель Тобина максимальной ожидаемой доходности из всех портфелей риска не более 15% и его доходность.
. Найти портфель Тобина максимальной ожидаемой доходности из всех портфелей риска не более 15% и его доходность.
|
|
|
Решение. Из уравнения эффективной границы портфеля Тобина:
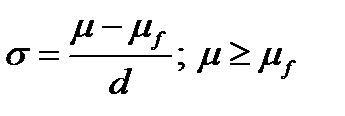 получаем:
получаем: 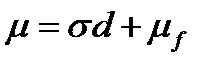 .
.
Максимальная ожидаемая доходность 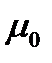 при заданных значениях безрисковой ставки
при заданных значениях безрисковой ставки 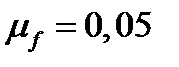 и максимальном значении риска
и максимальном значении риска 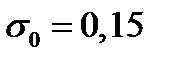 равна:
равна: 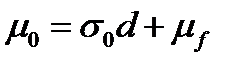 .
.
Рынок в данной задаче такой же,как и в задаче 12. Найденное в задаче 12 значение 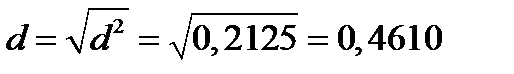 . Следовательно, максимальная ожидаемая доходность равна:
. Следовательно, максимальная ожидаемая доходность равна:
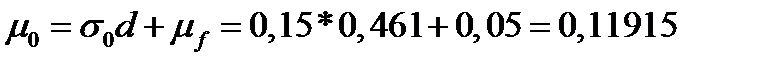 .
.
Найденное в задаче 12 значение обратной матрицы 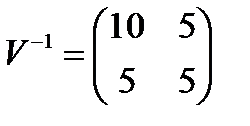 .
.
Соответствующий рисковый портфель равен:
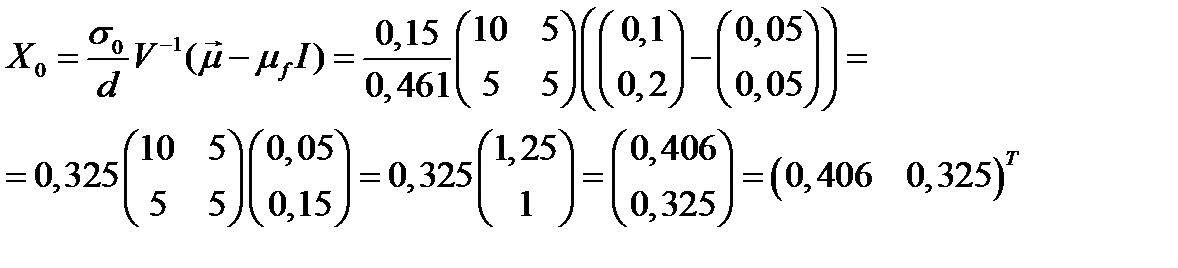 .
.
Ценовая доля безрисковой бумаги равна:
 .
.
Портфель Тобина ожидаемой доходности 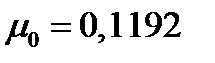 и риска
и риска 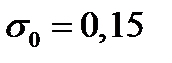 имеет вид:
имеет вид:
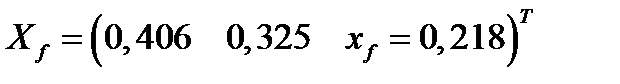 .
.
Ответ. 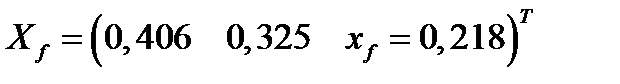 ;
; 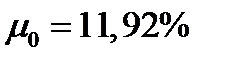 .
.
Дата добавления: 2020-04-08; просмотров: 1052; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
