Портфель Марковица минимального риска произвольной доходности.
Задача состоит в том, чтобы найти вектор 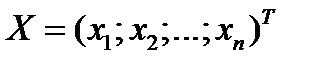 , такой что:
, такой что:
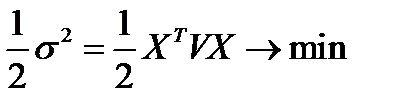
при условии
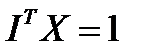 ,
,
где 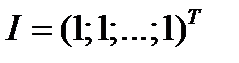 - вектор-столбец, состоящий из единиц.
- вектор-столбец, состоящий из единиц.
Применяя метод множителей Лагранжа, находим, что портфель минимального риска имеет вид:
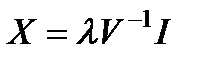 ,
,
где 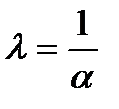 - множитель Лагранжа и
- множитель Лагранжа и  .
.
Отсюда получаем, что квадрат риска портфеля минимального риска
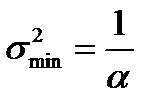 ,
,
а риск портфеля минимального риска
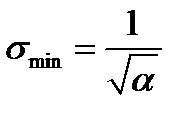 .
.
Пусть 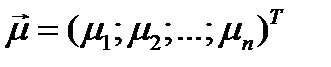 - вектор ожидаемых доходностей бумаг портфеля. Тогда ожидаемая доходность портфеля минимального риска равна:
- вектор ожидаемых доходностей бумаг портфеля. Тогда ожидаемая доходность портфеля минимального риска равна:
 .
.
Обозначая через 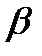 число
число
 ,
,
получаем значение ожидаемой доходности портфеля минимального риска
 .
.
Пример 8. На рынке присутствуют два активас ожидаемыми доходностями: 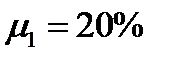 ,
,  и ковариационной матрицей
и ковариационной матрицей 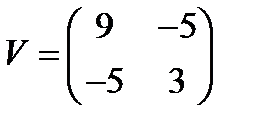 . Найти портфель минимального риска , его риск и доходность.
. Найти портфель минимального риска , его риск и доходность.
Решение. Портфель минимального риска имеет вид:
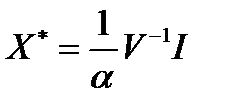 .
.
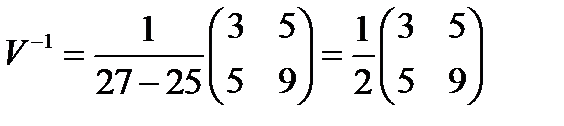 ;
;  ;
;
Константа  .
.
Портфель минимального риска равен:
 .
.
Его риск равен:
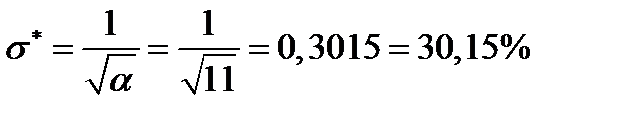 .
.
Доходность портфеля минимального риска равна:
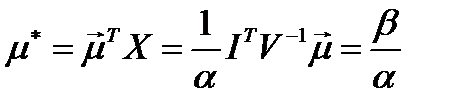 .
.
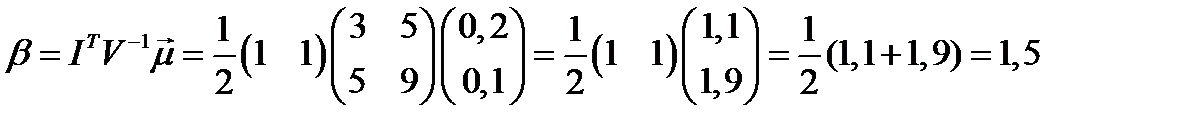 .
.
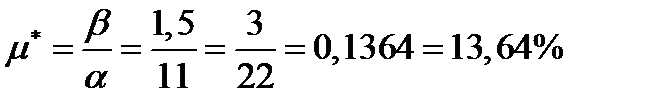 .
.
Ответ. 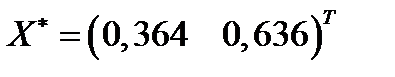 ;
; 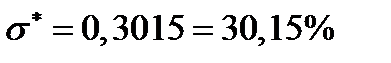 ;
; 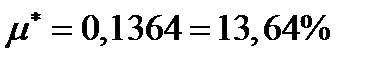
Пример 9. На рынке присутствуют два актива: 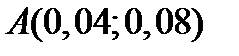 и
и 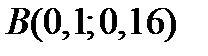 . Коэффициент корреляции активов
. Коэффициент корреляции активов 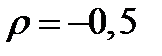 . Найти портфель минимального риска, его доходность и риск.
. Найти портфель минимального риска, его доходность и риск.
Решение. Составим ковариационную матрицу. Ее элементы равны:
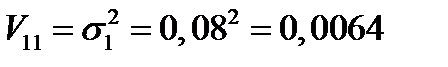 ;
; 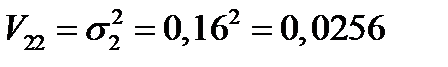 ;
;  .
.
Ковариационная матрица равна:
 .
.
Обратная матрица равна:
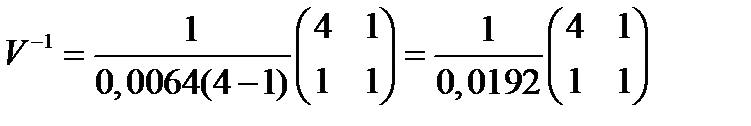 .
.
Константа 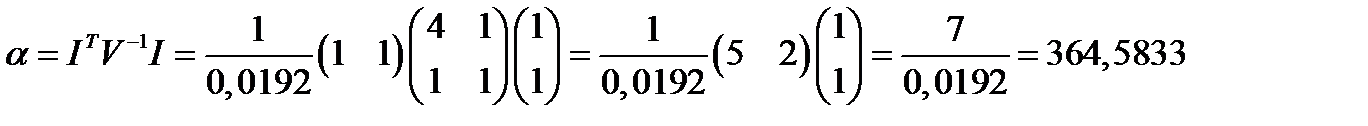 .
.
Портфель минимального риска равен:
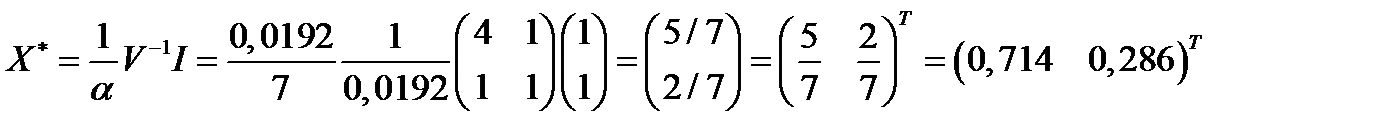 .
.
Вектор ожидаемых доходностей активов равен:  .
.
Константа 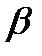 равна:
равна:
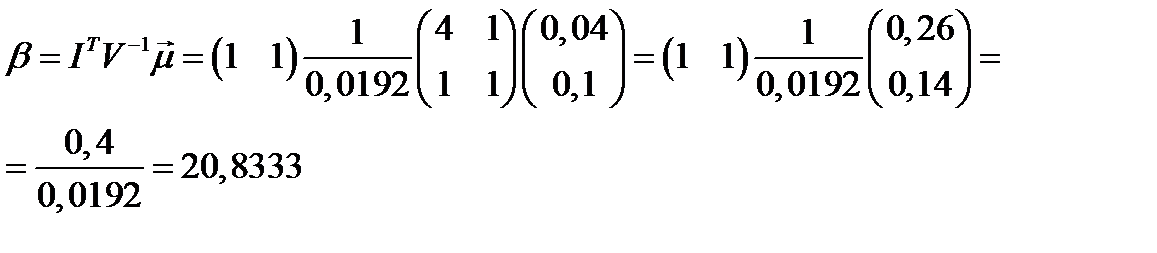
Доходность портфеля минимального риска равна:
|
|
|
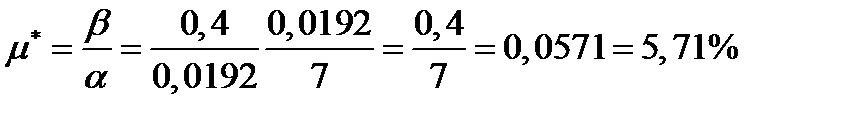 .
.
Риск портфеля минимального риска равен:
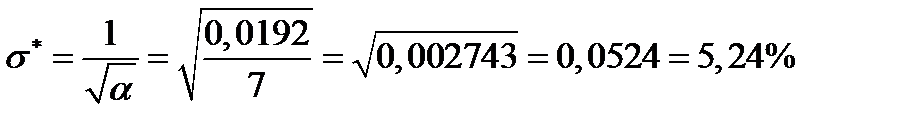 .
.
Ответ. 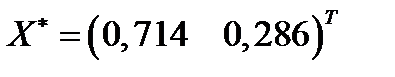 ;
; 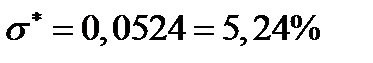 ;
; 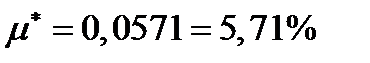 .
.
Пример 10. На рынке присутствуют три активас ожидаемыми доходностями: 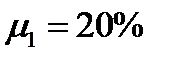 ,
,  ,
, 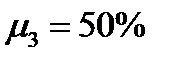 и ковариационной матрицей
и ковариационной матрицей 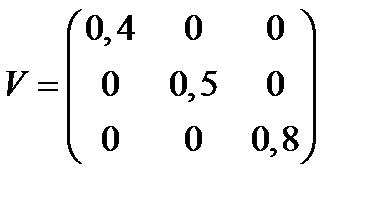 .
.
Найти портфель минимального риска и его риск и доходность.
Решение. Портфель минимального риска имеет вид:
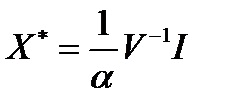 .
.
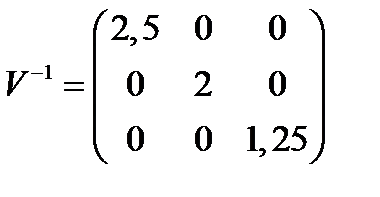 ;
; 

Портфель минимального риска равен:
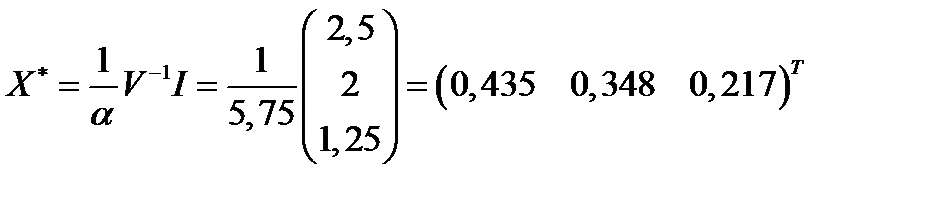 .
.
Его риск равен:
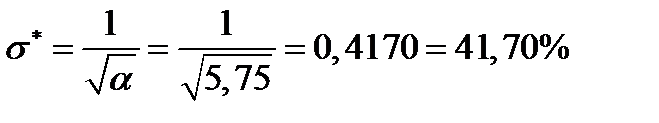 .
.
Доходность портфеля минимального риска равна:
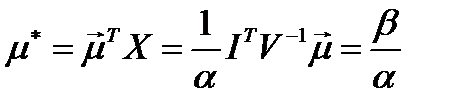 .
.
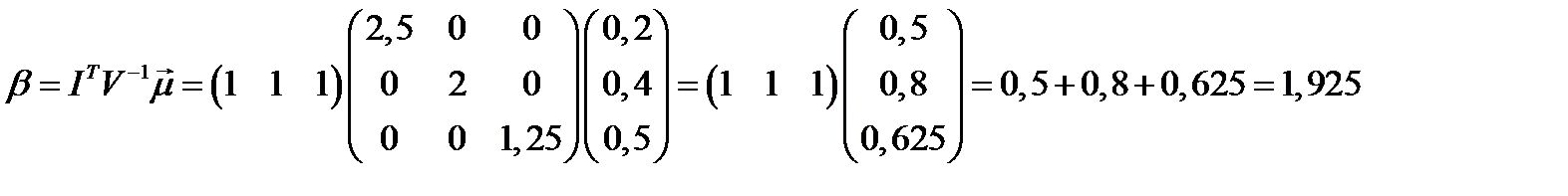
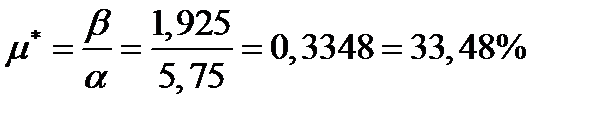
Ответ. 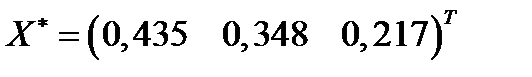 ;
; 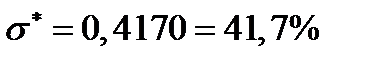 ;
; 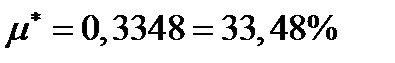 .
.
Портфель Марковица минимального риска при заданной доходности
Требуется найти портфель 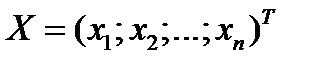 , который минимизировал бы риск
, который минимизировал бы риск  и обеспечивал заданную величину
и обеспечивал заданную величину 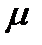 ожидаемой доходности:
ожидаемой доходности:
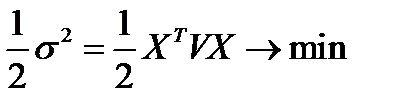
при условиях:
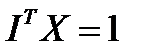 ,
,
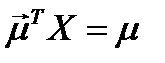 .
.
Предполагается, что ковариационная матрица 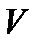 является положительно определенной, то есть для любого ненулевого вектора
является положительно определенной, то есть для любого ненулевого вектора 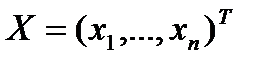 справедливо неравенство
справедливо неравенство
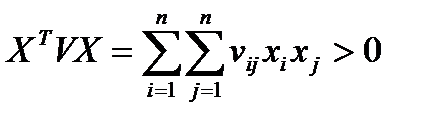 .
.
Как известно из линейной алгебры, в этом случае матрица 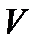 является невырожденной ( поскольку согласно критерию Сильвестра её определитель
является невырожденной ( поскольку согласно критерию Сильвестра её определитель  ) и обратная к ней матрица
) и обратная к ней матрица 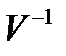 также является положительно определенной.
также является положительно определенной.
Предполагается также, что вектор ожидаемых доходностей активов, обращающихся на рынке 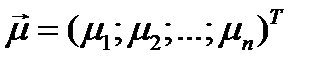 не коллинеарен вектору
не коллинеарен вектору  , то есть доходности не всех активов одинаковы.
, то есть доходности не всех активов одинаковы.
Введем следующие обозначения для констант:
|
|
|
 ;
;  ;
; 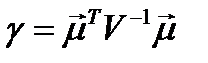 ;
; 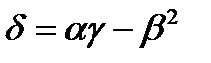 .
.
В силу положительной определенности матрицы 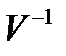 справедливы соотношения:
справедливы соотношения:
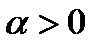 ;
; 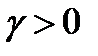 ;
; 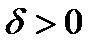 .
.
Для решения поставленной задачи составим функцию Лагранжа и найдем ее экстремум:
 ,
,
где 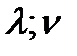 - множители Лагранжа. Приравнивая к нулю производную по
- множители Лагранжа. Приравнивая к нулю производную по 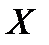 и учитывая условия, наложенные на
и учитывая условия, наложенные на 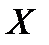 , получим систему уравнений:
, получим систему уравнений:
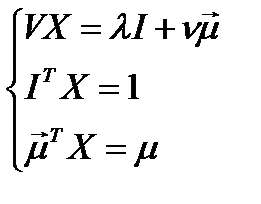 .
.
Выразим 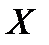 из первого уравнения:
из первого уравнения:
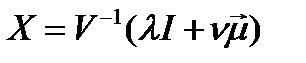
и подставим во второе и третье уравнения:
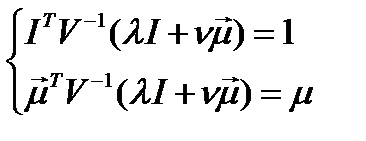 .
.
Раскрывая скобки с учетом введенных выше обозначений, получим систему:
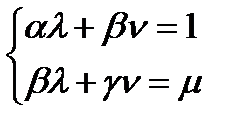 .
.
Определитель данной системы равен:
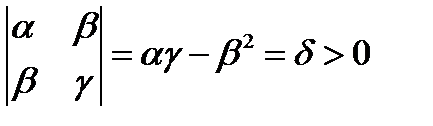 .
.
Следовательно, она имеет единственное решение:
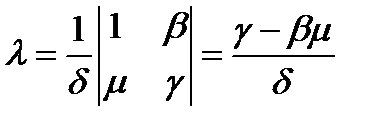 ;
;  .
.
Таким образом, портфель минимального риска при заданной его ожидаемой доходности 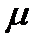 равен:
равен:
 .
.
Минимальное значение квадрата риска равно:
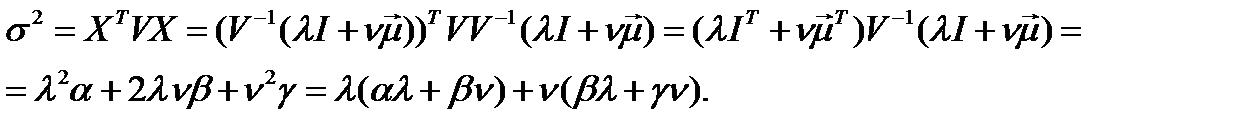
Так как
 и
и  ,
,
то:
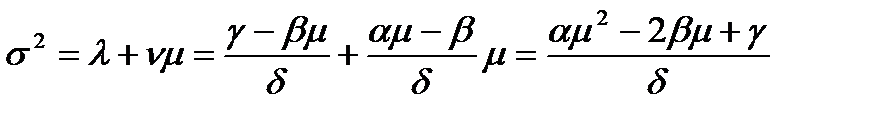 .
.
Для каждого значения ожидаемой доходности 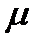 имеется единственный портфель
имеется единственный портфель 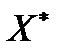 , обеспечивающий минимальное значение риска:
, обеспечивающий минимальное значение риска:
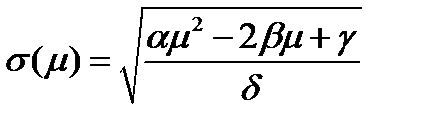 .
.
Полученная зависимость 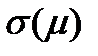 называется уравнением минимальной границы, а график функции
называется уравнением минимальной границы, а график функции 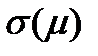 называется минимальной границей и представляет собой верхнюю ветвь гиперболы с асимптотами:
называется минимальной границей и представляет собой верхнюю ветвь гиперболы с асимптотами:
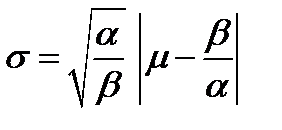
и минимумом в точке
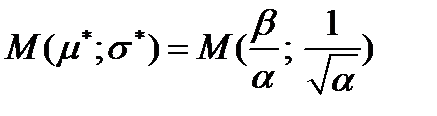 .
.
Рис. 4.1. Минимальная граница риска
Минимальной границей является кривая AMB. Асимптоты изображены штриховыми линиями (крупная штриховка). Точки на более доходной части минимальной границы, то есть на кривой МВ, являются эффективной границей.
|
|
|
Пример 11. На рынке присутствуют три активас ожидаемыми доходностями: 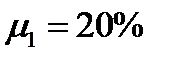 ,
,  ,
, 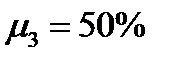 и ковариационной матрицей
и ковариационной матрицей 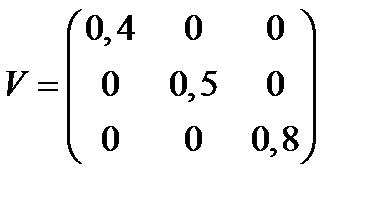 .
.
Найти портфель минимального риска с ожидаемой доходностью 0,4 и его риск.
Решение. Рынок в данной задаче такой же,как и в задаче 7. Заданная доходность портфеля 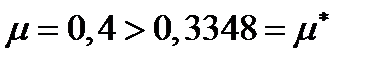 . Следовательно, портфель минимального риска при заданной его ожидаемой доходности
. Следовательно, портфель минимального риска при заданной его ожидаемой доходности 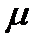 равен:
равен:
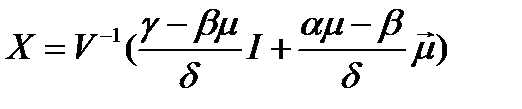 .
.
Минимальное значение риска равно:
 .
.
Значения 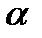 и
и 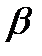 были найдены в задаче 7:
были найдены в задаче 7:  ,
, 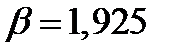 .
.
Найдем значения 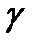 и
и 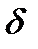 .
.
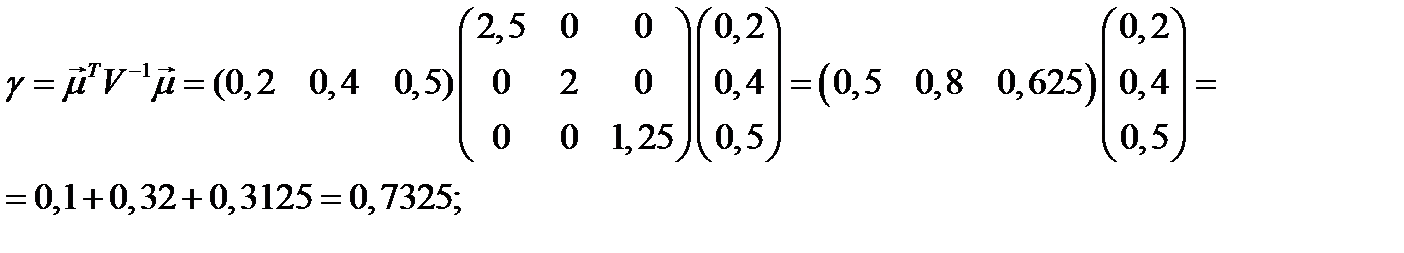
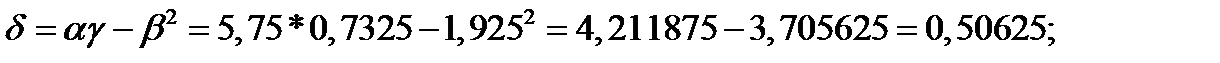

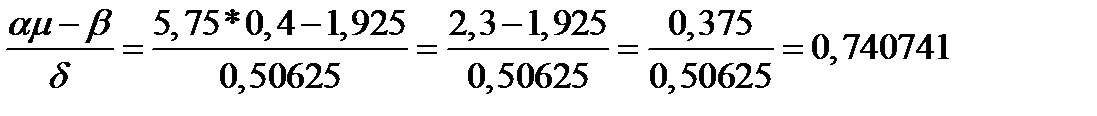 .
.
Искомый портфель минимального риска при заданной его ожидаемой доходности 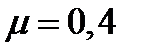 таков:
таков:

Таким образом, 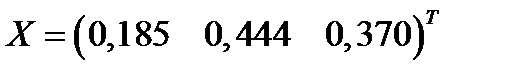
Риск данного портфеля равен:
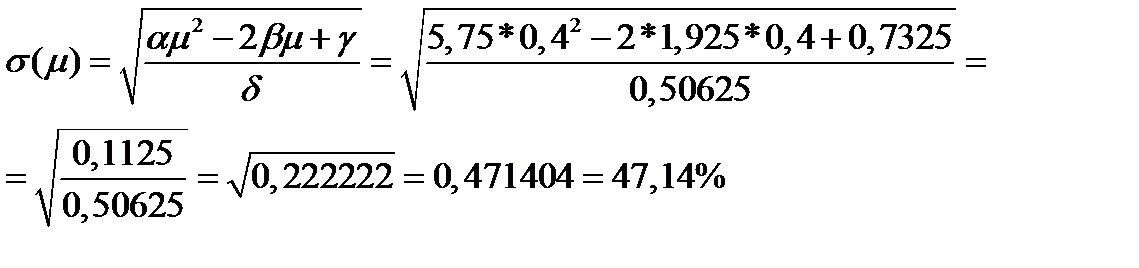
Ответ. 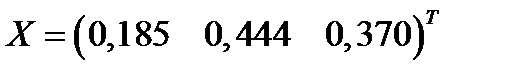 ,
, 
Дата добавления: 2020-04-08; просмотров: 723; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
