Уравнения плоскостей в пространстве общее, явное,
В векторной форме, параметрические. Вектор нормали. Формула расстояния
От точки до плоскости. Нахождение угла между плоскостями пространстве.
Уравнение плоскости:
1) Общее
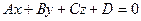 , где
, где 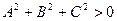
2) Явное
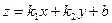 , где k1 и k2 – угловые коэффициенты.
, где k1 и k2 – угловые коэффициенты.
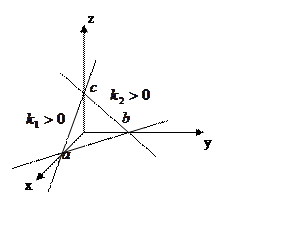
3) В векторной форме

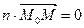 , где n – нормальный вектор плоскости, а
, где n – нормальный вектор плоскости, а 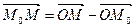
4) Параметрические:

Вектор нормали:
Вектор нормали к поверхности в данной точке — это единичный вектор, приложенный к данной точке и параллельный направлению нормали.
Нормальный вектор – вектор перпендикулярный плоскости 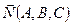 .
.
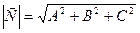
Формула расстояния от точки до плоскости:
Плоскость 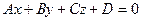 и точка
и точка 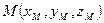
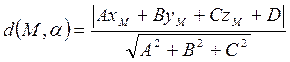
Нахождение угла между плоскостями в пространстве:
Пусть даны две плоскости:
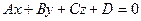 и
и 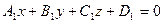
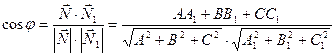
Дифференцируемость функции нескольких переменных.
Дифференциал от функции нескольких переменных. Частные производные.
Дифференцируемость функции нескольких переменных:
Функция f дифференцируема, если существует главная линейная часть приращения, то есть существуют такие 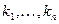 , что α – бесконечно малая по сравнению с длиной вектора
, что α – бесконечно малая по сравнению с длиной вектора 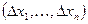 .
.
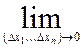
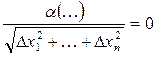
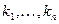 - частные производные
- частные производные
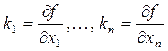
Дифференциал от функции нескольких переменных:
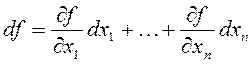
Частные производные:
Производная функции по какой-либо переменной.
Пример:
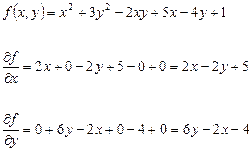
Уравнения прямых в пространстве общие, параметрические, канонические,
В векторной форме. Направляющий вектор.
Нахождение угла между прямыми, между прямой и плоскостью пространстве.
|
|
|
Уравнения прямых:
1) Общие
Прямую в пространстве можно задать так же, как линию пересечения двух плоскостей.
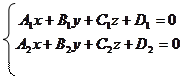
2) Канонические
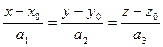 , где
, где 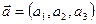 - направляющий вектор прямой.
- направляющий вектор прямой.
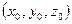 - точка прямой L (может быть любой).
- точка прямой L (может быть любой).
3) Параметрические
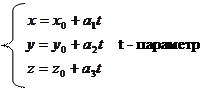
4) В векторной форме
Пусть 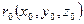 - радиус вектор точки М0(x0, y0, z0) и
- радиус вектор точки М0(x0, y0, z0) и 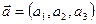 - направляющий вектор прямой.
- направляющий вектор прямой.
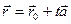
Направляющий вектор:
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.
Нахождение угла между прямыми в пространстве:
Даны две прямые:
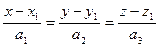 и
и 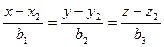 , где
, где 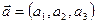 и
и 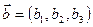 направляющие векторы соответствующих прямых.
направляющие векторы соответствующих прямых.
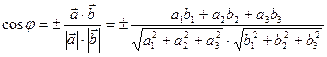
Нахождение угла между прямой и плоскостью пространстве:
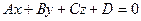 и прямая
и прямая 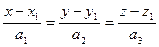
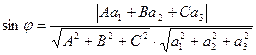
Градиент и его свойство ортогональности. Формулы касательной прямой к кривой
В плоскости и касательной плоскости к поверхности в пространстве.
Вывод формул касательных к кривым 2-го порядка.
Определение:
Градиент – вектор функции, координаты которого равны значениям частных производных.
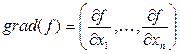
Свойство градиента:
Градиент перпендикулярен линии поверхности уровня. Строго говоря перпендикулярен не к линии поверхности, а к касательной.
|
|
|
Формула касательной к кривой в плоскости:
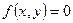
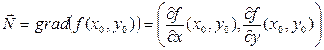
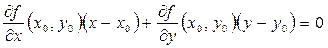
Формула касательной плоскости к поверхности в пространстве:
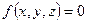
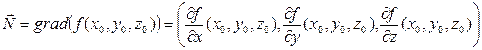
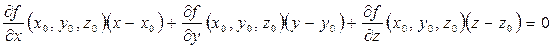
Вывод формулы для касательной к эллипсу:
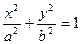 - уравнение эллипса.
- уравнение эллипса.
Эллипс – линия уровня функции 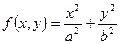
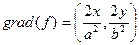
В точке 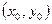
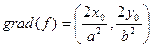
Касательная 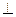
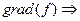 возьмем
возьмем 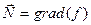 в точке
в точке 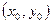
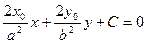
С-?
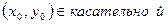
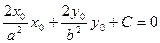
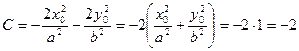
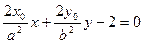
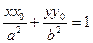
Вывод формулы для касательной к гиперболе:
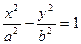 - уравнение эллипса.
- уравнение эллипса.
Гипербола – линия уровня функции 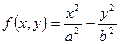
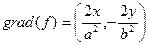
В точке 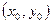
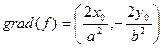
Касательная 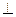
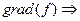 возьмем
возьмем 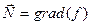 в точке
в точке 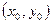
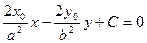
С-?
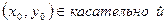
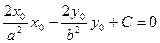
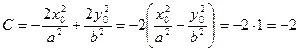
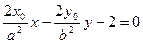
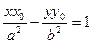
Вывод формулы для касательной к параболе:
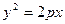 - уравнение эллипса.
- уравнение эллипса.
Гипербола – линия уровня функции 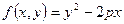
Соответствует: 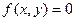
Пусть 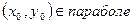
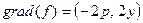
В точке 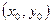
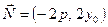
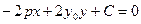
С-?
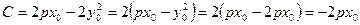
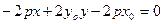
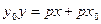
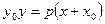
Дата добавления: 2019-09-13; просмотров: 161; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
