Интегрирование рациональных выражений. Деление многочленов.
Для интегрирования рациональной функции 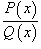 , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:
, где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:
1. Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
2. Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
3. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
4. Вычислить интегралы от простейших дробей.
Интегрирование тригонометрических выражений.
Вычисление интеграла вида 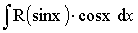
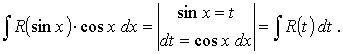
Вычисление интеграла вида 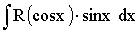
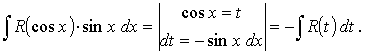
Вычисление интеграла вида 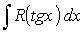 .
.
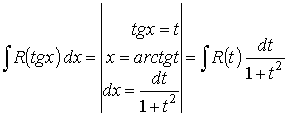 .
.
Вычисление интеграла 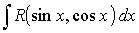 , где sin x и cos x входят в чётных степенях
, где sin x и cos x входят в чётных степенях
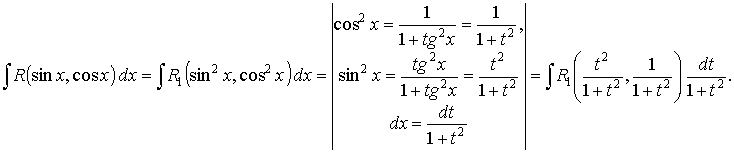
Интегрирование рациональных выражений. Разложение в сумму элементарных дробей.
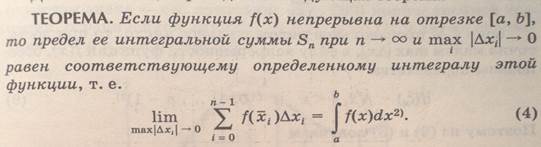 | |||
 | |||
Интегрирование рациональных выражений. Интегрирование элементарных дробей.
Элементарными называются дроби следующих четырех типов:
I. 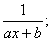 III.
III. 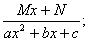
II. 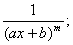 IV.
IV. 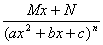
m, n – натуральные числа (m 2, n 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. 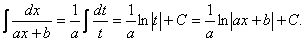
II. 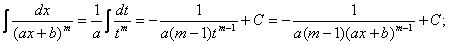
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
|
|
|
Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида 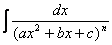 можно путем выделения в знаменателе полного квадрата представить в виде
можно путем выделения в знаменателе полного квадрата представить в виде 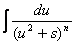 . Сделаем следующее преобразование:
. Сделаем следующее преобразование:
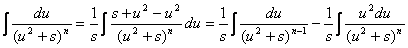 .
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 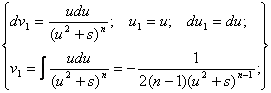
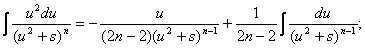
Для исходного интеграла получаем:
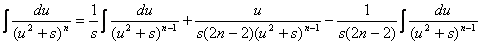
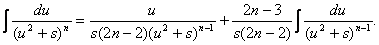
Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл 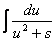 .
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u 2 + s приводится к табличному 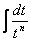 , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
, а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Теорема о формуле Ньютона-Лейбница.
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Если 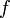 непрерывна на отрезке непрерывна на отрезке 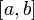 и и 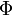 — ее любая первообразная на этом отрезке, то имеет место равенство — ее любая первообразная на этом отрезке, то имеет место равенство
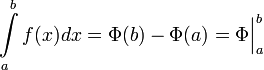
|
Гиперболические функции.
Гиперболические функции задаются следующими формулами:
|
|
|
· гиперболический синус:
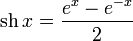
(в англоязычной литературе обозначается 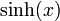 )
)
· гиперболический косинус:
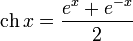
(в англоязычной литературе обозначается 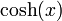 )
)
· гиперболический тангенс:
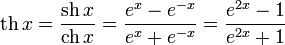
(в англоязычной литературе обозначается 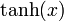 )
)
· гиперболический котангенс:
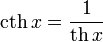
Иногда также определяются
· гиперболические секанс и косеканс:
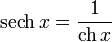
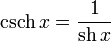
Геометрическое определение
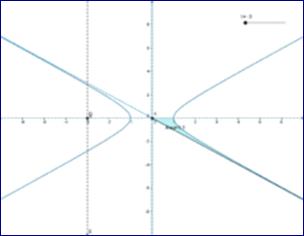

Параметризация гиперболического синуса (анимация).
Ввиду соотношения 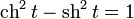 гиперболические функции дают параметрическое представление гиперболы
гиперболические функции дают параметрическое представление гиперболы 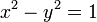 (
( 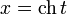 ,
, 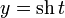 ). При этом аргумент
). При этом аргумент 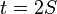 , где
, где 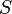 — площадь криволинейного треугольника
— площадь криволинейного треугольника 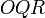 , взятая со знаком «+», если сектор лежит выше оси
, взятая со знаком «+», если сектор лежит выше оси 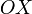 , и «−» в противоположном случае. Очевидно, что и гиперболические функции определяются через этот параметр, например, уравнения гиперболического синуса в параметрической форме:
, и «−» в противоположном случае. Очевидно, что и гиперболические функции определяются через этот параметр, например, уравнения гиперболического синуса в параметрической форме: 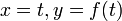 , где
, где 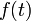 — ордината точки гиперболы, соответствующей площади
— ордината точки гиперболы, соответствующей площади 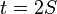 . Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
Дата добавления: 2019-09-13; просмотров: 184; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
