Формула Муавра и извлечение корней из комплексных чисел
Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:
где 
— модуль, а 
— аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.
Аналогичная формула применима также и при вычислении корней 
-ой степени из ненулевого комплексного числа:
Отметим, что корни -й степени из ненулевого комплексного числа всегда существуют, и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника, вписанного в окружность радиуса 
с центром в начале координат (см. рисунок).
Матрицы: определение, арифметика матриц. Связь матриц и систем линейных
Уравнений.
Ма́трица — совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.
Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины стробцов.
Матрица – прямоугольная таблица, предполагающая выполнение арифметических действий.
Арифметика матриц:
1) сложение (Складываются матрицы только одного размера)
2)умножение матрицы на число:
3) Умножение матриц (перемножать матрицы можно только тогда, когда длина строки первой матрицы равна высоте столбцов второй матрицы.)
Умножается «строка» на «столбец» так же как скалярно перемножаются два вектора.
Связь матриц и систем линейных уравнений
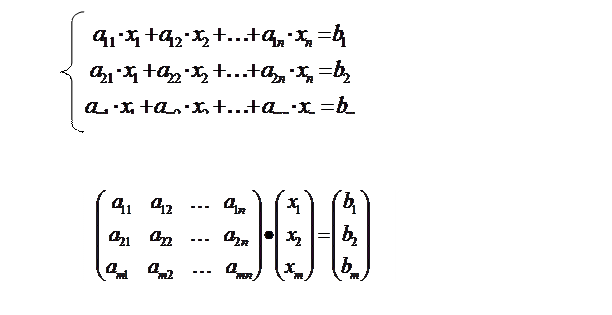
Алгебраические свойства матриц. Понятие обратной матрицы. Применение
Обратных матриц к решению систем линейных уравнений.
Матричные операции
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица 
такая, что её прибавление к другой матрице A не изменяет A, то есть
Все элементы нулевой матрицы равны нулю.
Возводить в степень можно только квадратные матрицы.
- Ассоциативность сложения:
- Коммутативность сложения:
- Ассоциативность умножения:
- Вообще говоря, умножение матриц некоммутативно:
. Используя это свойство, вводят коммутатор матриц. - Дистрибутивность умножения относительно сложения:
- С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.
- Свойства операции транспонирования матриц:
, если обратная матрица 
существует.
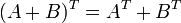
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме 
, где матрица A имеет размерность n на n и ее определитель отличен от нуля.
Так как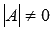 
, то матрица А – обратима, то есть, существует обратная матрица 
. Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных 
. Так мы получили решение системы линейных алгебраических уравнений матричным методом.
Дата добавления: 2019-09-13; просмотров: 233; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!