Формула интегрирования по частям и ее вывод.
Понятие первообразной. Свойства первообразных.
Функция F(х) называется первообразной для функции f(х) на заданном промежутке J, если для всех х из этого промежутка F`(х)= f(х). Так функция F(х)=х3 первообразная для f(х)=3х2 на (- ∞ ; ∞ ).
Так как, для всех х ~R справедливо равенство: F`(х)=(х3)`=3х2
Свойства первообразной
· Первообразная суммы равна сумме первообразных
· Первообразная произведения константы и функции равна произведению константы и первообразной функции
· Достаточным условием существования первообразной у заданной на отрезке функции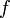 
является непрерывность 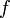на этом отрезке
· Необходимыми условиями существования являются принадлежность функции 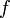первому классу Бэра и выполнение для неё свойства Дарбу
· У заданной на отрезке функции любые две первообразные отличаются на постоянную.
(Основное свойство первообразной функции)
Если F(х) одна из первообразных для функции f(х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С - любое действительное число.
Доказательство:
Пусть F`(х) = f (х), тогда (F(х)+С)`= F`(х)+С`= f (х), для х Є J.
Допустим существует Φ(х)- другая первообразная для f (х) на промежутке J, т.е. Φ`(х) = f (х),
тогда (Φ(х)- F(х))` = f (х) – f (х) = 0, для х Є J.
Это означает, что Φ(х)- F(х) постоянна на промежутке J.
Следовательно, Φ(х)- F(х) = С.
Откуда Φ(х)= F(х)+С.
Это значит, что если F(х) - первообразная для функции f (х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С - любое действительное число.
Следовательно, любые две первообразные данной функции отличаются друг от друга постоянным слагаемым.
|
|
|
Понятие неопределенного интеграла. Свойства неопределенного интеграла.
Неопределенным интегралом 
называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. 
или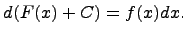 
Неопределённый интегра́л для функции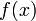 
— это совокупность всех первообразных данной функции.
Если функция 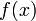определена и непрерывна на промежутке 
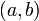и 
— её первообразная, то есть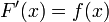 
при 
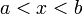, то
,
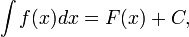
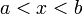где С — произвольная постоянная.
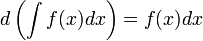
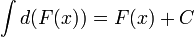
Свойства:
1.Постоянный множитель можно выносить за знак интеграла:
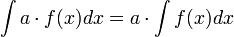
2.Интеграл суммы функций равен сумме интегралов этих функций:
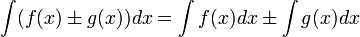
3.
Если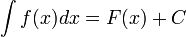 
, то и 
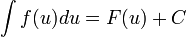, где 
— произвольная функция, имеющая непрерывную производную
Основные методы нахождения неопределенных интегралов.
1. Метод введения нового аргумента. Если
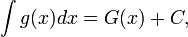
то
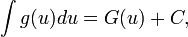
где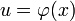 
— непрерывно дифференцируемая функция.
2. Метод разложения. Если
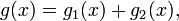
то
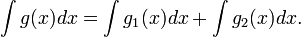
3. Метод подстановки. Если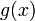 
— непрерывна, то, полагая
|
|
|
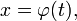
где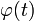 
непрерывна вместе со своей производной 
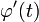, получим
4. Метод интегрирования по частям. Есл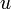и 
и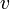 
— некоторые дифференцируемые функции от 
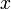, то
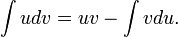
Формула интегрирования по частям и ее вывод.
Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации.
Формула интегрирования по частям следующая 
.
Дата добавления: 2019-09-13; просмотров: 188; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!