Понятие интегральной суммы. Определение определенного интеграла.
Понятие интегральной суммы.
Пусть на отрезке [a, в] задана функция у = f(x). Разобьем отрезок на п элементарных отрезков точками деления а = х0, х1, х2, …, хп = в. На каждом элементарном отрезке [xi-1, xi] выберем произвольную точку Сi и положим
| n |
∆хi = xi — xi-1, где i = 1,2,…,п, в каждой точке Сi найдем значение функции f(Ci), составим произведения f(C1)∆x1, f(C2)∆x2, …, f(Ci)∆xi, …, f(Cn)∆xn, рассмотрим сумму этих произведений:
| I=1 |
f(C1)∆x1 + f(C2)∆x2 + … + f(Ci)∆xi + … + f(Cn)∆xn = Σ f(Ci)∆xi.
Эту сумму будем называть интегральной суммой для функции у=f(x) на отрезке [а, в]. Интегральная сумма зависит как от способа разбиения отрезка [a, в] на п частей так и от выбора точек С1, С2, …, Сп на каждом элементарном отрезке разбиения.
Определение: Пусть y= f( x) – непрерывная на отрезке [ a, b] функция и ( Sn) – последоватльность интегральных сумм. Тогда limn →∞ Sn называют определённым интегралом (или просто интегралом) функции f ( x ) по отрезку [ a , b ] и обозначается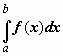 
( Определенным интегралом от заданной функции 
f (x) называется предел интегральных сумм, т.е.:
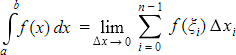
Определенный интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a, x = b и графиком функции f (x) ).
Приложение определенного интеграла к вычислению площади области
В декартовых координатах.
Если плоская фигура ограничена прямыми x = a, x = b, a < b, и кривыми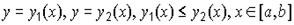 
, то ее площадь вычисляется по формуле 
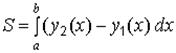(рис. 10.1).
|
|
|
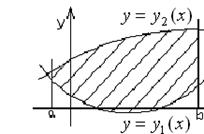Рис. 10.1.
| Аналогично можно рассматривать фигуру относительно оси ОУ.
В некоторых случаях границы х = а и х = b могут вырождаться в точку пересечения кривых  .
В сложных случаях область следует разбить на фигуры, границы которых удовлетворяют указанным соотношениям.
|
При решении задач удобно придерживаться следующего порядка:
- построить в декартовых координатах фигуру, площадь которой требуется найти;
- найти точки пересечения кривых, образующих границу области для определения пределов интегрирования;
- записать формулу для вычисления и найти площадь.
Теорема о производной определенного интеграла по верхнему пределу
Интегрирования.
 | |||
 | |||
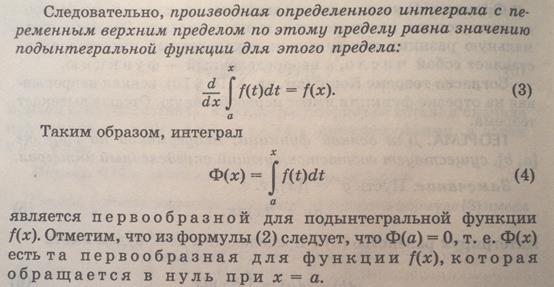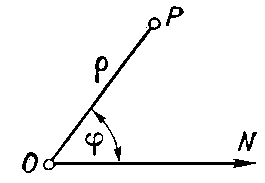
Полярные координаты и вывод формулы площади криволинейного сектора.
Полярные координаты
точки на плоскости, два числа, которые определяют положение этой точки относительно некоторой фиксированной точки О (полюс) и некоторого фиксированного луча ON (полярной оси), исходящего из полюса. Эти числа ρ (полярный радиус) и φ (полярный угол) равны соответственно расстоянию от О до Р и углу между ON и ОР. Угол φ называют иногда амплитудой, точки Р. Для взаимно однозначного соответствия между точками плоскости и парами П. к. изменение П. к. обычно ограничивают промежутками: 0 ≤ ρ ≤ + ∞; 0 ≤ φ < 2π (при этом полярный угол полюса остаётся неопределённым). Если же однозначности предпочитают непрерывность (чтобы при непрерывном движении точки её П. к. изменялись также непрерывно), то в качестве полярного угла берут величину φ0 + kπ (k — произвольное число), где φ0 есть угол NOP, а полярному радиусу приписывают знак + или —, смотря по тому, совпадает ли направление луча ОР с направлением, получающимся в результате поворота оси ON на угол, равный выбранному значению полярного угла, или же эти направления противоположны.
|
|
|
Дата добавления: 2019-09-13; просмотров: 692; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!