Дифференциальные уравнения первого порядка.

⇐ ПредыдущаяСтр 13 из 13

УравнениеF(x, y, y ') = 0, где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.

Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y'(x)) ≡ 0 для всех x из (a,b) .

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.

Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x₀) = y₀, называется задачей Коши (или начальной задачей).

Условие y(x₀) = y₀ — начальное условие.

Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.

Общее решение уравнения, записанное в неявной форме Φ(x,y) = C, называется общим интегралом уравнения.

Частное решение уравнения, записанное в неявной форме Φ(x,y) = 0, называется частным интегралом уравнения.

Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:

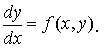
Уравнения первого порядка часто записывают в дифференциальной форме:

M(x, y)dx + N(x, y)dy = 0.

Решение такого уравнения можно искать как в виде y = y(x), так и в виде x = x(y).

Дифференциальные уравнения высших порядков.

Дифференциальное уравнение n-го порядка имеет вид F(x,y,y′,y′′,…,y(n))=0F(x,y,y′,y″,…,y(n))=0

Для уравнения второго порядка y′′=f(x,y,y′)y″=f(x,y,y′) начальные условия имеют вид y|x=x0=y0,y′|x=x0=y′0,y|x=x0=y0,y′|x=x0=y0′, где x0,y0,y′0x0,y0,y0′ — данные числа. В этом случае теорема существования и единственности геометрически означает, что через данную точку

M0(x0,y0)M0(x0,y0) плоскости OxyOxy с данным тангенсом угла наклона касательной y0y0 проходит единственная кривая.

Общим решением дифференциального уравнения n-го порядка называется множество всех его решений, определяемое формулой y=φ(x,C1,C2,…,Cn)y=φ(x,C1,C2,…,Cn), содержащей nn произвольных постоянных C1,C2,…,CnC1,C2,…,Cn таких, что если заданы начальные условия, то найдутся такие значения C˜1,C˜2,…,C˜nC~1,C~2,…,C~n , что y=φ(x,C˜1,C˜2,…,C˜n) y=φ(x,C~1,C~2,…,C~n) будет являться решением уравнения, удовлетворяющим этим начальным условиям.

Любое решение, получаемое из общего решения при конкретных значениях произвольных постоянных C1,C2,…,CnC1,C2,…,Cn называется частным решением дифференциального уравнения.

Д.у Бернулли. Однородное д.у.

Обыкновенное дифференциальное уравнение вида:

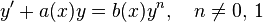
называется уравнением Бернулли (пр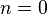и или 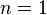получаем неоднородное или однородное линейное уравнение).

Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение 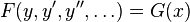— однородно, если .

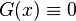В случае, если 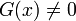, говорят о неоднородном дифференциальном уравнении.

Дата добавления: 2019-09-13; просмотров: 147; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8 9 10 11 1213

Мы поможем в написании ваших работ!