Достаточное условие вогнутости ( выпуклости ) функции.
Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:
если f '' ( x ) > 0 для любого x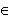 
( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x 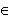( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
П р и м е р. Рассмотрим график функции y = x3 :
Эта функция является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x3.
Асимптоты графика и функции.
Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.
Прямая 
называется вертикальной асимптотой графика функции 
, если хотя бы одно из предельных значений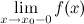 
или 
равно 
или 
.
Замечание. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Прямая 
называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений 
или 
равно 
.
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Прямая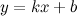 
называется наклонной асимптотой графика функции , если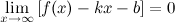 
Дифференциал функции. Применение дифференциала в приближенных вычислениях.
Дифференциал (от лат. differentia — разность, различие) — линейная часть приращения функции.
Обычно дифференциал функции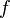 
обозначается 
.
Дифференциал в точке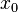 
обозначается 
, а иногда 
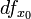или 
, а также , если значение 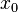ясно из контекста.
Соответственно, значение дифференциала в точке 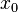от 
может обозначаться как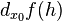 
, а иногда 
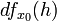или 
, а также 
, если значение 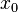ясно из контекста.
Приращение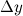 
функции представимо в виде:
где функция 
является бесконечно малой функцией при стремлении аргумента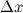 
к нулю. Так как 
, то
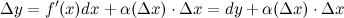
В силу того, что второе слагаемое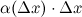 
является бесконечно малым, то им можно пренебречь, а поэтому
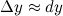
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула:
Первообразная функции. Таблица интегралов.
Первообрзной данной функции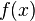 
называют такую 
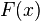, производная которой (на всей области определения) равна 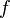, то есть 
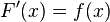. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Первообразные важны тем, что позволяют вычислять интегралы. Если 
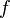— первообразная интегрируемой функции , то:
Таблица интегралов
Дата добавления: 2019-09-13; просмотров: 175; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!