Предел функции в точке. Определение. Геометрический смысл.
Построим график функции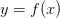 
и отметим на нём точки 
и 
.
Предел функции 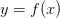в точке 
существует и равен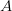 
, если для любой 
-окрестности точки 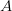можно указать такую 
-окрестность точки 
, что для любого 
из этой -окрестности значение 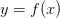будет находится в -окрестности точки .
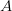Первый и второй замечательные пределы.
Первый замечательный предел:
Второй замечательный предел:
, или 
.
Свойства функций, непрерывных на отрезке. Теоремы Вейерштрасса, Коши.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897) - немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке 
выполняется условие - 
.
Свойство 2: Функция, непрерывная на отрезке , принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения 
и 
, что 
, причем 
.
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например - 
).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке , принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция 
непрерывна в точке 
, то существует некоторая окрестность точки 
, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция - непрерывная на отрезке и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где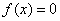 
.
|
|
|
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) - немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Свойство 7: Если функция определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция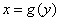 
тоже однозначна, монотонна и непрерывна.
Задачи, приводящие к понятию производной: о касательной, о скорости движения.
Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s=s(t), где t— время (в секундах), s(t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).
Решение . Предположим, что в момент времени t тело находилось в точке M.
Дадим аргументу t приращение Δt и рассмотрим ситуацию в момент времени t+Δt. Координата материальной точки станет другой, тело в этот момент будет находиться в точке P:OP=s(t+Δt).
|
|
|
Значит, за Δt секунд тело переместилось из точки M в точку P. Имеем: MP=OP−OM=s(t+Δt)−s(t). Полученную разность мы назвали в приращением функции: s(t+Δt)−s(t)=Δs. Итак, MP=Δs(м). Нетрудно найти среднюю скорость vср движения тела за промежуток времени [t;t+Δt]: vср=Δs/Δt (м/с).
А что такое скорость v(t) в момент времени t (ее называют мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени [t;t+Δt] при условии, что Δt выбирается все меньше и меньше; точнее: при условии, что Δt→0. Это значит, что v(t)=lim(Δt→0vср).
Итак,
v=lim(Δt→0) Δs/Δt
Задача 2 (о касательной к графику функции). Дан график функции y=f(x). На нем выбрана точка M(a;f(a)), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
Решение . Дадим аргументу приращение Δx и рассмотрим на графике точку P с абсциссой a+Δx. Ордината точки P равна f(a+Δx). Угловой коэффициент секущей MP, т. е. тангенс угла между секущей и осью x, вычисляется по формуле kсек=Δy/Δx.
Если мы теперь устремим Δx к нулю, то точка P начнет приближаться по кривой к точке M. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной kкас=lim(Δx→0)kсек будет вычисляться по формуле kкас=lim(Δx→0)kсек. Используя приведенную выше формулу для kсек, получаем:
|
|
|
kкас=lim(Δx→0)Δy/Δx.
Дата добавления: 2019-09-13; просмотров: 278; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!