Определение производной. Пример нахождения производной функции, исходя из определения производной.
Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференцированием.
Определение производной функции через предел
Пусть в некоторой окрестности точки 
определена функция 
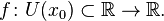Производной функции 
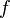в точке 
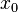называется предел, если он существует,
Основные правила дифференцирования.
1. Константу можно выносить за знак производной.
2. Производная суммы/разности.
Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.
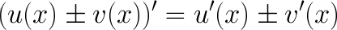
3. Производная произведения.
4. Производная частного.
Производная сложной и обратной функции.
Производная сложной функции.
Производная сложной функции равна производной этой функции по промежуточному аргументу 
, умноженной на производную от промежуточного аргумента по основному аргументу 
.
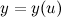и 
имеют производные соответственно в точках 
и 
. Тогда
Обратная функция: Пусть функция y = f(x) взаимно однозначна в интервале (a, b), содержащем точку x0. Пусть в точке x0 она имеет конечную и отличную от нуля производную f '(x0). Тогда обратная функция x = g(y) также имеет производную в соответствующей точке y0 = f(x0), причем
|
|
|
g '(y0) = 1/ f '(x0)
Таблица производных.
Логарифмическое дифференцирование.
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для нахождения производных степенных, рациональных и некоторых иррациональных функций.
Рассмотрим этот подход более детально. Пусть дана функция y=f(x). Возьмем натуральные логарифмы от обеих частей:
lny=lnf(x).
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.
(lny)′=(lnf(x))′,⇒1yy′(x)=(lnf(x))′.
Отсюда видно, что искомая производная равна
y′=y(lnf(x))′=f(x)(lnf(x))′.
Такая производная от логарифма функции называется логарифмической производной.
Данный метод позволяет также эффективно вычислять производные показательно-степенных функций, то есть функций вида
y=u(x)v(x),
где u(x) и v(x) − дифференцируемые функции от x.
Производные высших порядков.
Если функция 
имеет производную в каждой точке своей области определения, то ее производная 
есть функция от . Функция 
, в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом 
. Таким образом
|
|
|
Производные более высоких порядков определяются аналогично. То есть производная 
-го порядка функции 
есть первая производная от производной 
-го порядка этой функции:
Дата добавления: 2019-09-13; просмотров: 579; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!