Бесконечно большая величина. Свойства бесконечно больших. Связь между бесконечно малыми и бесконечно большими величинами.
Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция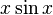 
, неограниченная с обеих сторон, не является бесконечно большой при 
.
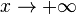Последовательность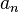 
называется бесконечно большой, если 
.
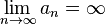Функция называется бесконечно большой в окрестности точки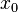 
, если 
.
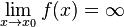Функция называется бесконечно большой на бесконечности, если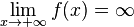 
, либо 
.
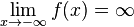Как и в случае бесконечно малых, необходимо отметить, что ни одно отдельно взятое значение бесконечно большой величины не может быть названо как «бесконечно большое» — бесконечно большая величина — это функция, которая лишь в процессе своего изменения может стать больше произвольно взятого числа.
· Сумма бесконечно больших последовательностей одного знака есть бесконечно большая последовательность того же знака.
· Сумма бесконечно большой и ограниченной последовательностей есть бесконечно большая последовательность.
· Произведение бесконечно больших последовательностей есть бесконечно большая последовательность.
· Произведение бесконечно большой последовательности на константу есть бесконечно большая последовательность.
Теорема о связи между бесконечно большой и бесконечно малой функциями:
|
|
|
Если функция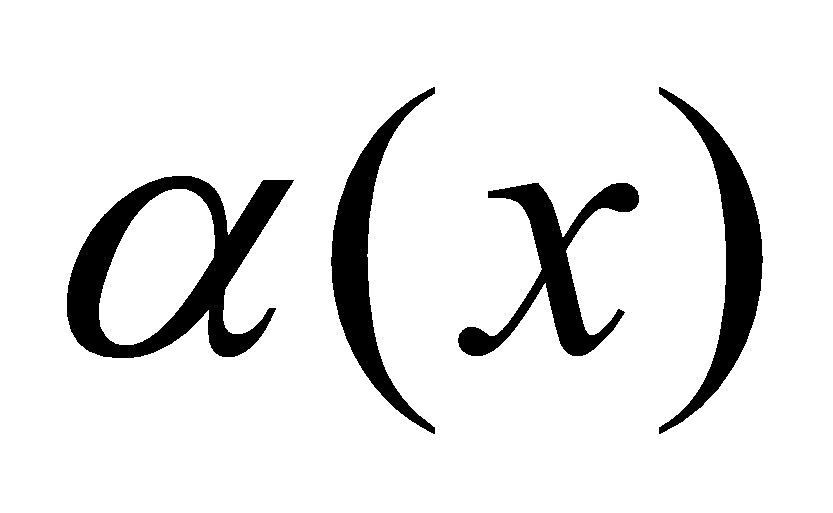 
- функция бесконечно малая ( 
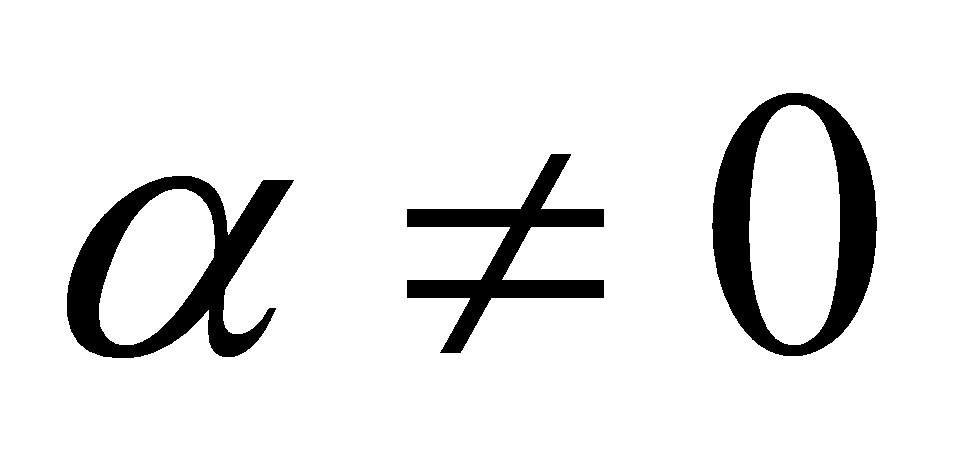), то функция 
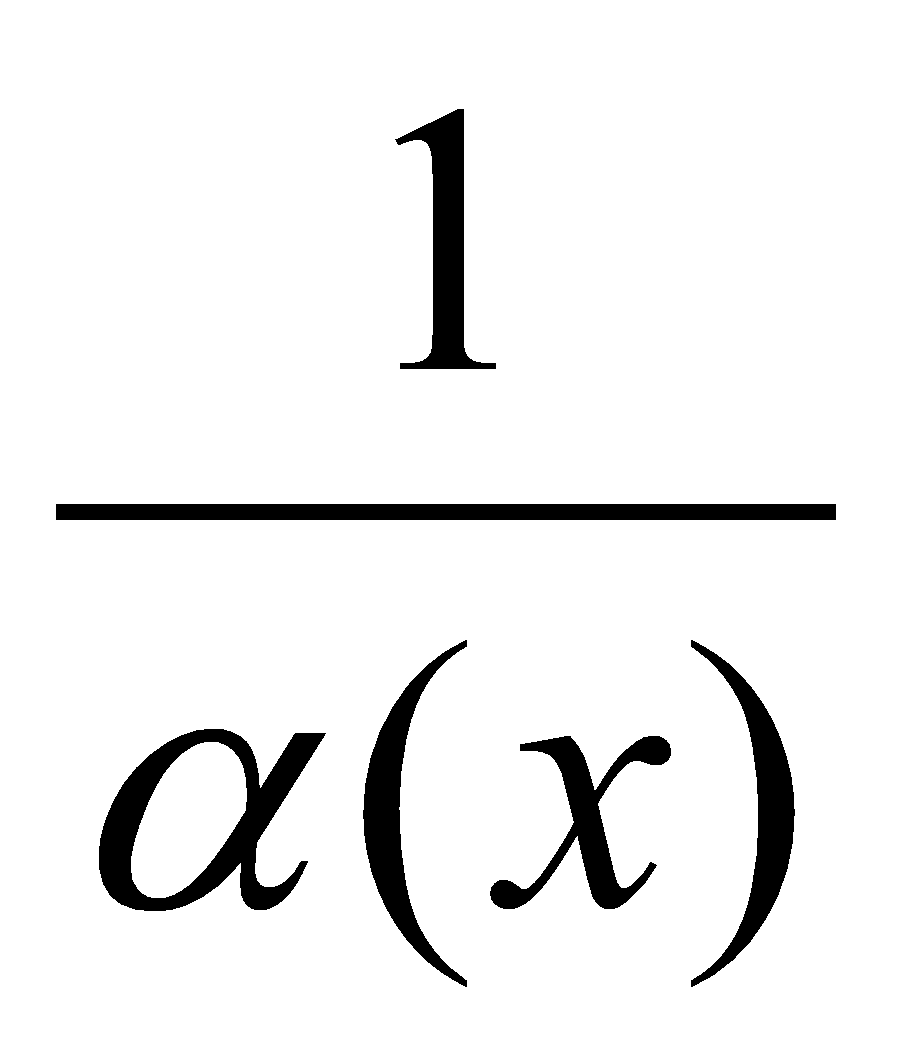есть бесконечно большая функция и наоборот.
9. Правила раскрытия неопределённостей ∞:∞, 0:0, заданных отношениями многочленов.
Чтобы найти предел, надо раскрыть неопределенность вида бесконечность на бесконечность. Для этого и в числителе, и в знаменателе выносим за скобки степень с наибольшим показателем. Затем сокращаем на нее.
1)
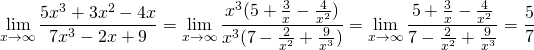
В дальнейшем просто делим почленно числитель и знаменатель (то есть каждое слагаемое) на старшую степень икса.
2)
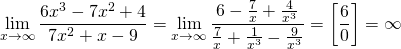
А теперь сделаем выводы. Пределы на неопределенность бесконечность на бесконечность сводятся к одному из трех вариантов:
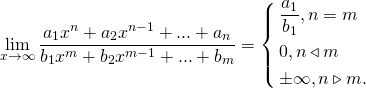
Неопределенность вида 0/0
Если при подстановке предельного значения х получаем
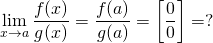
то такое выражение называется неопределенностью вида ноль на ноль. Неопределенность 0 на 0 надо убрать.
Чтобы избавиться от неопределенности вида ноль на ноль, заданной отношением двух многочленов, надо и в числителе, и в знаменателе выделить критический множитель и сократить на него. Чтобы выделить критический множитель — то есть множитель, равный нулю при предельном значении х — нужно многочлены разложить на множители.
Способы разложения многочлена на множители:
|
|
|
— вынесение общего множителя за скобки;
— по формулам сокращенного умножения;
— группировка;
— по теореме о разложении квадратного трехчлена на множители.
Дата добавления: 2019-09-13; просмотров: 223; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!